
- My presentations

Auth with social network:
Download presentation
We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower. Thank you!
Presentation is loading. Please wait.
An Introduction to Graph Theory
Published by Doreen Willis Modified over 8 years ago
Similar presentations
Presentation on theme: "An Introduction to Graph Theory"— Presentation transcript:

Chapter 8 Topics in Graph Theory

Chapter 9 Graphs.

Lecture 5 Graph Theory. Graphs Graphs are the most useful model with computer science such as logical design, formal languages, communication network,

22C:19 Discrete Math Graphs Fall 2010 Sukumar Ghosh.

22C:19 Discrete Math Graphs Fall 2014 Sukumar Ghosh.

Midwestern State University Department of Computer Science Dr. Ranette Halverson CMPS 2433 – CHAPTER 4 GRAPHS 1.

13 May 2009Instructor: Tasneem Darwish1 University of Palestine Faculty of Applied Engineering and Urban Planning Software Engineering Department Introduction.

1 Slides based on those of Kenneth H. Rosen Slides by Sylvia Sorkin, Community College of Baltimore County - Essex Campus Graphs.

Graph Graph Types of Graphs Types of Graphs Data Structures to Store Graphs Data Structures to Store Graphs Graph Definitions Graph Definitions.

Computational Geometry Seminar Lecture 1

Introduction to Graphs

Discrete Structures Chapter 7A Graphs Nurul Amelina Nasharuddin Multimedia Department.

CTIS 154 Discrete Mathematics II1 8.2 Paths and Cycles Kadir A. Peker.

W. D. Grover TRLabs & University of Alberta © Wayne D. Grover 2002, 2003 Graph theory and routing (initial background) E E Lecture 4.

Drawing of G. Planar Embedding of G Proposition Proof. 1. Consider a drawing of K 5 or K 3,3 in the plane. Let C be a spanning cycle. 2. If the.

Problem: Induced Planar Graphs Tim Hayes Mentor: Dr. Fiorini.

Chapter 4 Graphs.

Discrete Mathematics Lecture 9 Alexander Bukharovich New York University.

22C:19 Discrete Math Graphs Spring 2014 Sukumar Ghosh.
About project
© 2024 SlidePlayer.com Inc. All rights reserved.
Introduction to Graph Theory
Last updated: June 7, 2024
- Graph Theory
Baeldung Pro comes with both absolutely No-Ads as well as finally with Dark Mode , for a clean learning experience:
>> Explore a clean Baeldung
Once the early-adopter seats are all used, the price will go up and stay at $33/year.
1. Overview
In this tutorial, we’ll discuss some of the most important data structures in computer science – graphs .
We’ll first study the basics of graph theory, in order to familiarize ourselves with its conceptual foundation. We’ll then study the types of graphs that we can find in our machine learning applications.
At the end of this tutorial, we’ll know what a graph is and what types of graphs exist. We’ll also know what are the characteristics of the graph’s primitive components.
2. The Basics of Graph Theory
2.1. the definition of a graph.
A graph is a structure that comprises a set of vertices and a set of edges. So in order to have a graph we need to define the elements of two sets: vertices and edges.
The vertices are the elementary units that a graph must have, in order for it to exist . It’s customary to impose on graphs the condition that they must have at least one vertex, but there’s no real theoretical reason why this is the case. Vertices are mathematical abstractions corresponding to objects associated with one another by some kind of criterion.
Edges instead are optional, in the sense that graphs with no edges can still be defined . An edge, if it exists, is a link or a connection between any two vertices of a graph, including a connection of a vertex to itself. The idea behind edges is that they indicate, if they are present, the existence of a relationship between two objects, that we imagine the edges to connect.
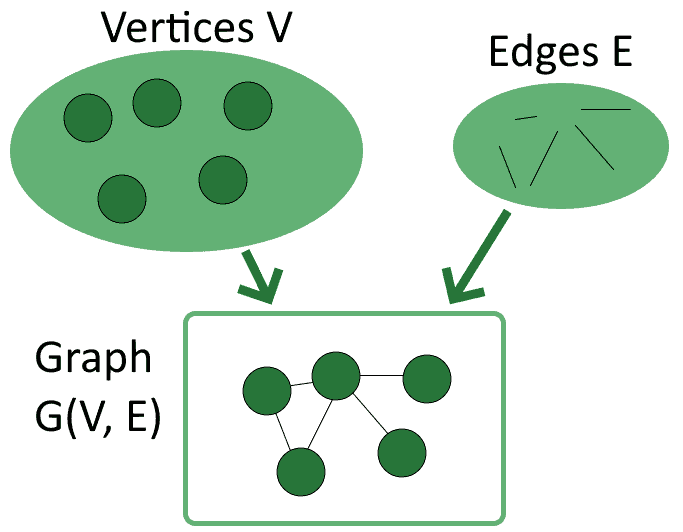
A brief note on terminology before we proceed further: graphs are a joint subject of study for both mathematics and network theory . The terms used in the two disciplines differ slightly, but they always refer to the same concepts. For this article, we’ll be using the terminology of mathematics, but we can use a conversion table to translate between the two if necessary.
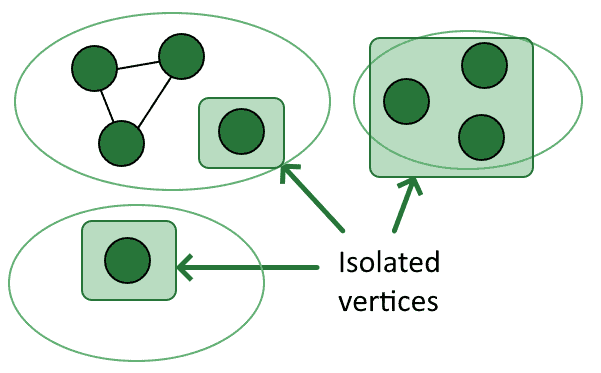
2.2. General Properties of Vertices
We’re now going to focus in more detail about what characteristics vertices and edges possess. Let’s start with the vertices first.
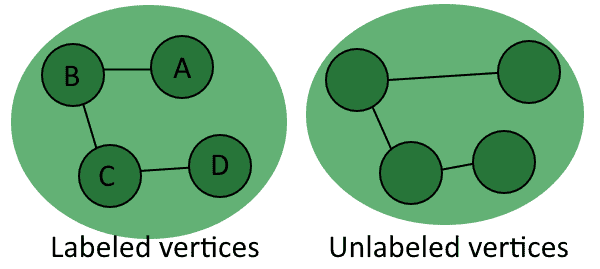
2.3. Labels of Vertices
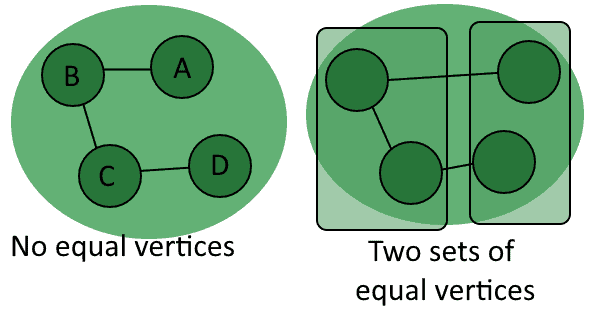
Vertices can also have values associated with them. These values can take any format and there are no specific restrictions for them. A vertex with an associated value is called a labeled vertex, while a vertex with no associated value is called unlabeled :
In general, we can distinguish any two unlabeled vertices exclusively on the basis of their paired vertices. The comparison between labeled vertices requires us instead to study both the pairs of vertices and the values assigned to them:
2.4. General Properties of Edges
We can now study the characteristics of edges. In contrast with vertices, edges can’t exist in isolation. This derives from the consideration that graphs themselves require vertices in order to exist, and that edges exist in relation to a graph.
An edge can connect any two vertices in a graph. The two vertices connected by an edge are called endpoints of that edge . By its definition, if an edge exists, then it has two endpoints.
Graphs whose edges connect more than two vertices also exist and are called hypergraphs . This tutorial doesn’t focus on them, but we have to mention their existence because of their historical and contemporary importance for the development of knowledge graphs.

2.5. Endpoints, Directions, Loops
It’s possible to further distinguish between the two endpoints of an edge, according to whether they point towards a vertex or rather away from it. We call an edge going towards a vertex an incoming edge, while we call an edge originating from a vertex an outgoing edge :
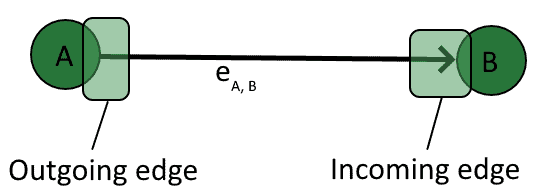
The advantage of this type of thinking is that it translates well to adjacency matrices of graphs .
Furthermore, an edge can simultaneously be an incoming edge and an outgoing edge for the same vertex. In this case, we call that edge a loop.
Loops are a special kind of edge and aren’t present in all graphs. We call graphs without loops simple graphs, in order to distinguish them from the others:
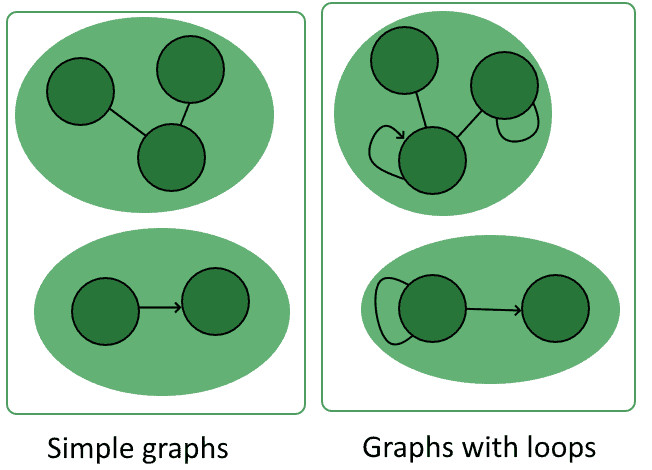
2.4. Paths in a Graph
A graph with a non-empty set of edges has paths, which consist of sequences of edges that connect two vertices . We can call paths that relate to sequences of directed edges, unsurprisingly, directed paths; paths related to undirected edges however don’t have a special name.
One way to look at the relationship between paths and graphs is to imagine that each graph is a labyrinth and that each of its vertices is an intersection:
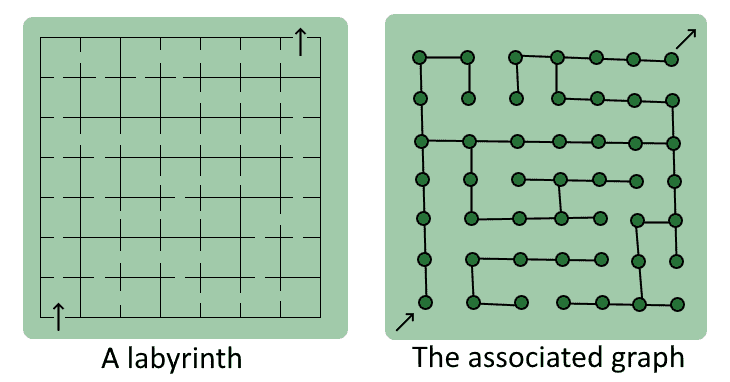
In this model, the starting vertex of a path corresponds to the entrance of the maze, and the target vertex corresponds to the exit. If we use this conceptual framework we can then imagine traversing the labyrinth and leaving a trail behind, which we then call a path .
One special kind of path is the one that traverses all vertices in a graph, and that’s called a Hamiltonian path . Hamiltonian paths aren’t necessarily present in all graphs. We call graphs that contain Hamiltonian paths traceable because it’s possible to leave a full trace that covers all of their vertices:
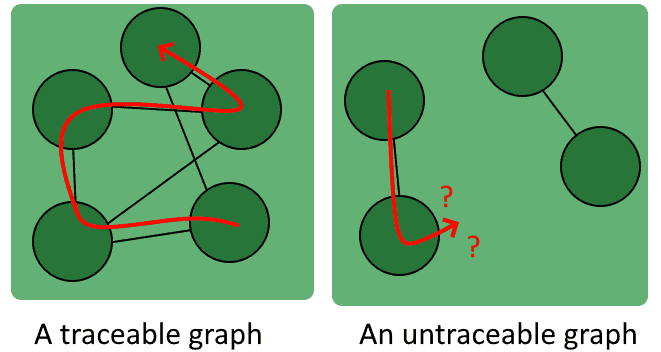
Finally, we can mention that paths whose start and end vertices coincide are special, and are called cycles . It’s important to detect cycles in graphs because the algorithms for finding paths may end up looping over them indefinitely.
One last note on why paths are particularly important in computer science. This is because there are efficient algorithmic ways such as Dijkstra’s algorithm and A* that allow us to easily find the shortest paths. This, in turn, allows the computer resolution of problems such as the optimization of processes, logistics, and the processing of search queries.
3. Types of Graphs
3.1. the empty graph.
We mentioned before that graphs exist only if their set of vertices is not null. Their set of edges, however, may as well be empty. If this is the case, we say that the graph is empty:
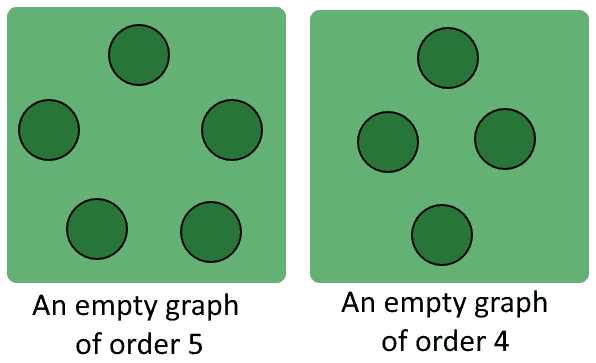
3.2. The Directed Graph
Directed graphs have the characteristic that they model real-world relationships well for which we can’t freely interchange the subject and the object. As a general rule, if we aren’t sure whether a graph should be directed or undirected, then the graph is directed:
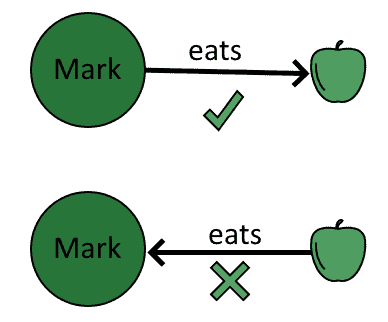
We can only traverse directed graphs in the directions of their existing directed edges.
Regarding directed graphs, we can briefly mention that there are general methods for determining whether a directed graph contains the maximum number of possible edges . This is important for reasons that have to do with the entropy of a directed graph .
3.3. The Undirected Graph
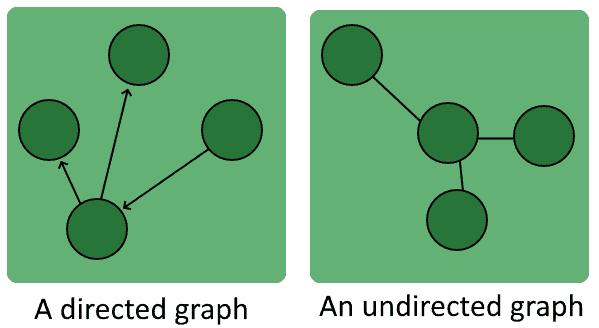
Undirected graphs allow their traversal between any two vertices connected by an edge. The same isn’t necessarily true for directed graphs.
3.4. The Connected and Disconnected Graphs
We can also discriminate graphs on the basis of the characteristics of their paths. For example, we can discriminate according to whether there are paths that connect all pairs of vertices, or whether there are pairs of vertices that don’t have any paths between them. We call a graph connected if there is at least one path between any two of its vertices:
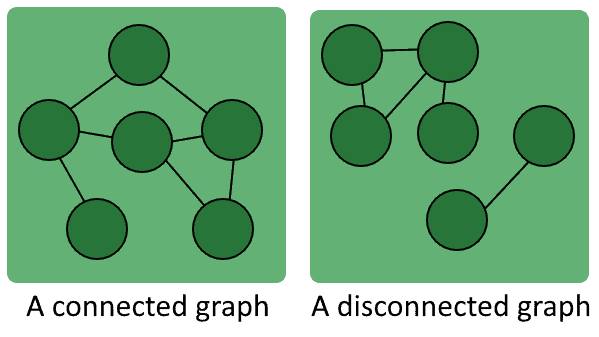
Similarly, we say that a graph is disconnected if there are at least two vertices separated from one another.
3.5. The Hamiltonian-Connected Graph
A Hamiltonian-connected graph is a graph for which there is a Hamiltonian path between any two of its vertices. Notice how connected graphs aren’t necessarily Hamiltonian-connected:
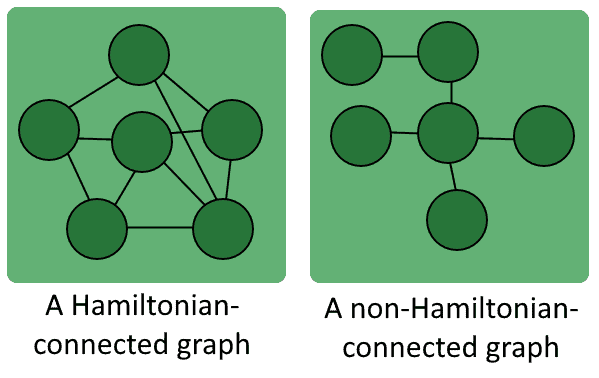
A Hamiltonian-connected graph is always a traceable graph, but the opposite isn’t necessarily true.
3.6. The Complete Graph
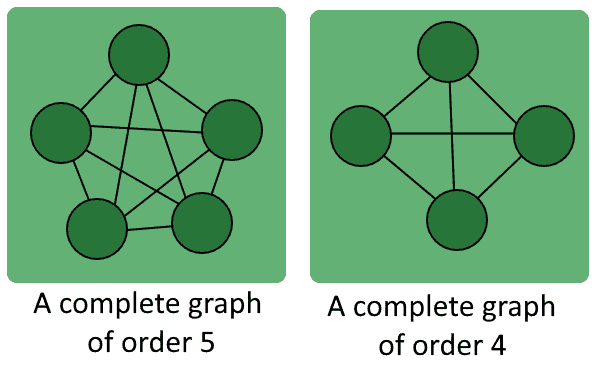
All complete graphs of the same order with unlabeled vertices are equivalent.
3.7. The Tournament
A tournament is a kind of complete graph that contains only directed edges:
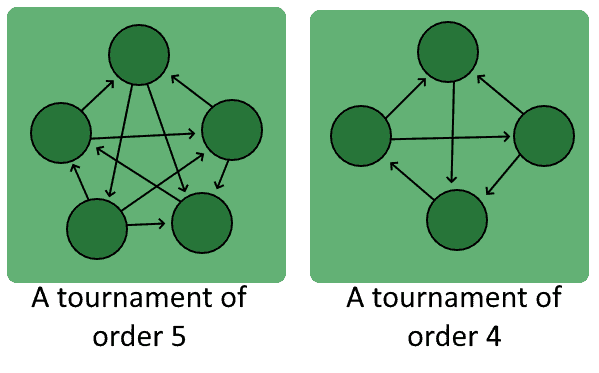
The name originates from its frequent application in the formulation of match composition for sports events.
3.8. The Weighted Graph
The final type of graph that we’ll see is a weighted graph. A weighted graph is a graph whose edges have a weight (that is, a numerical value) assigned to them:
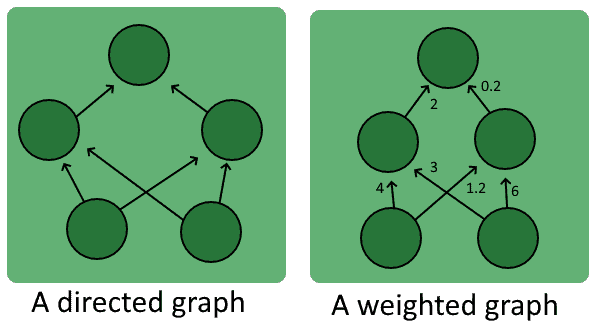
A typical weighted graph commonly used in machine learning is an artificial neural network . We can conceptualize neural networks as directed weighted graphs on which each vertex has an extra activation function assigned to it.
4. Conclusions
In this tutorial, we studied the conceptual bases of graph theory. We also familiarized ourselves with the definitions of graphs, vertices, edges, and paths.
We’ve also studied the types of graphs that we can encounter and what are their predictable characteristics in terms of vertices, edges, and paths.

IMAGES
VIDEO
COMMENTS
A simple graph does not have multiple edges or loops. Our book uses multigraph if loops aren't allowed and pseudograph if loops are allowed (whether or not they actually occur). Other books call it a multigraph [with / without] loops allowed. Prof. Tesler Ch. 1. Intro to Graph Theory Math 154 / Winter 2020 13 / 42
On an island, there are: k people who have blue eyes, everyone else has green eyes. At the start of the puzzle, no one on the island knows their own eye color. If a person on the island ever discovers they have blue eyes, that person must leave the island at dawn; anyone not making such a discovery always sleeps until after dawn. On the island ...
A walk in a graph G = (V, E) is a sequence of one or more nodes v₁, v₂, v₃, …, vₙ such that any two consecutive nodes in the sequence are adjacent. A closed walk in a graph is a walk from a node back to itself. (By convention, a closed walk cannot have length zero.) The length of the walk v₁, …, vₙ is n - 1. SF Sac SF, Sac
Formalizing Graphs An unordered pair is a set {a, b} of two elements a ≠ b. (Remember that sets are unordered.) For example, {0, 1} = {1, 0} An undirected graph is an ordered pair G = (V, E), where V is a set of nodes, which can be anything, and E is a set of edges, which are unordered pairs of nodes drawn from V. A directed graph (or digraph) is an ordered pair
graph theory is the study of graphs which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices or nodes and lines called edges that connect them. A graph may be undirected, meaning that there is no distinction between the two vertices associated with each edge, or its edges ...
Graph Theory1 IntroductionGraphs are an incredibly useful st. ucture in Computer Science! They arise in all sorts of applications, including scheduling, optimization, communications, and the design. and analysis of algorithms. In the next few lectures, we'll even show how two Stanford stu-dents used graph theory.
linear function M is a function from Rn to Rm that satisfies two properties: For all x; y. For all x 2. 2 R, M(x + y) = M(x) + M(y) R and all a 2 R (scalar) M(ax) = aM(x) Every linear function can be represented by a matrix. Every matrix is a linear function.
Geodesics. A geodesic from a to b is a path of minimum length The geodesic distance dab between a and b is the length of the geodesic If there is no path from a to b, the geodesic distance is infinite. For the graph. The geodesic distances are: dAB = 1, dAC = 1, dAD = 1, dBC = 1, dBD = 2, dCD = 2.
A walk in a graph G = (V, E) is a sequence of one or more nodes v₁, v₂, v₃, …, vₙ such that any two consecutive nodes in the sequence are adjacent. A closed walk in a graph is a walk from a node back to itself. (By convention, a closed walk cannot have length zero.) A path in a graph is walk that does not repeat any nodes.
Presentation on theme: "An Introduction to Graph Theory"— Presentation transcript: 1 An Introduction to Graph Theory BY DR. DALVINDER SINGH GOVT. COLLEGE ROPAR ... Lecture 5 Graph Theory. Graphs Graphs are the most useful model with computer science such as logical design, formal languages, communication network, ...
In our presentation, we will cover two real life applications of Graph Theory: Dijkstra Algorithm and PageRank. Dijkstra Algorithm is used to help find the shortest path from one point to another. PageRank is used to determine the most relevant webpages when a user makes a search in a search engine. In our presentation, we will cover two real ...
Presentation Transcript. Introduction • The three sections we are covering tonight have in common that they mostly contain definitions. Graph theory suffers from a large number of definitions that mathematicians use inconsistently. For instance, what some mathematicians call a graph, others call a simple graph.
Graph Theory. Definition. Baeldung Pro - CS - NPI EA (cat = Baeldung on Computer Science) Baeldung Pro comes with both absolutely No-Ads as well as finally with Dark Mode, for a clean learning experience: >> Explore a clean Baeldung. Once the early-adopter seats are all used, the price will go up and stay at $33/year. 1.
Presentation Transcript. Graph Theory Introducton. Graph Theory T. Serino Vertex: A point. An intersection of two lines (edges). Edge: A line (or curve) connecting two vertices. Loop: An edge that connects a vertex to itself only. Graph Theory T. Serino Ex) Represent the "Konigsberg Bridge" problem using a vertex-edge graph.