pythagorean theorem problem solving questions

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Christmas Worksheets
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• Kindergarten Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Pythagoras Theorem Questions

Welcome to our Pythagoras' Theorem Questions area. Here you will find help, support and questions to help you master Pythagoras' Theorem and apply it.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Pythagoras' Theorem Questions

Here you will find our support page to help you learn to use and apply Pythagoras' theorem.

Please note: Pythagoras' Theorem is also called the Pythagorean Theorem

There are a range of sheets involving finding missing sides of right triangles, testing right triangles and solving word problems using Pythagoras' theorem.

Using these sheets will help your child to:

• learn Pythagoras' right triangle theorem;
• use and apply the theorem in a range of contexts to solve problems.

Pythagoras' Theorem

Pythagoras' theorem - in more detail.

Pythagoras' theorem states that in a right triangle (or right-angled triangle) the sum of the squares of the two smaller sides of the triangle is equal to the square of the hypotenuse.

In other words, \[ a^2 + b^2 = c^2 \]

where c is the hypotenuse (the longest side) and a and b are the other sides of the right triangle.

What does this mean?

This means that for any right triangle, the orange square (which is the square made using the longest side) has the same area as the other two blue squares added together.

Other formulas that can be deduced from the Pythagorean theorem

As a result of the formula \[ a^2 + b^2 = c^2 \] we can also deduce that:

• \[ b^2 = c^2 - a^2 \]
• \[ a^2 = c^2 - b^2 \]
• \[ c = \sqrt{a^2 + b^2} \]
• \[ b = \sqrt {c^2 - a^2} \]
• \[ a = \sqrt {c^2 - b^2} \]

Pythagarean Theorem Examples

Example 1) find the length of the missing side..

In this example, we need to find the hypotenuse (longest side of a right triangle).

So using pythagoras, the sum of the two smaller squares is equal to the square of the hypotenuse.

This gives us \[ 4^2 + 6^2 = ?^2 \]

So \[ ?^2 = 16 + 36 = 52 \]

This gives us \[ ? = \sqrt {52} = 7.21 \; cm \; to \; 2 \; decimal \; places \]

Example 2) Find the length of the missing side.

In this example, we need to find the length of the base of the triangle, given the other two sides.

This gives us \[ ?^2 + 5^2 = 8^2 \]

So \[ ?^2 = 8^2 - 5^2 = 64 - 25 = 39 \]

This gives us \[ ? = \sqrt {39} = 6.25 \; cm \; to \; 2 \; decimal \; places \]

Pythagoras' Theorem Question Worksheets

The following questions involve using Pythagoras' theorem to find the missing side of a right triangle.

The first sheet involves finding the hypotenuse only.

A range of different measurement units have been used in the triangles, which are not drawn to scale.

• Pythagoras Questions Sheet 1
• PDF version
• Pythagoras Questions Sheet 2
• Pythagoras Questions Sheet 3
• Pythagoras Questions Sheet 4

Pythagoras' Theorem Questions - Testing Right Triangles

The following questions involve using Pythagoras' theorem to find out whether or not a triangle is a right triangle, (whether the triangle has a right angle).

If Pythagoras' theorem is true for the triangle, and c 2 = a 2 + b 2 then the triangle is a right triangle.

If Pythagoras' theorem is false for the triangle, and c 2 = a 2 + b 2 then the triangle is not a right triangle.

• Pythagoras Triangle Test Sheet 1
• Pythagoras Triangle Test Sheet 2

Pythagoras' Theorem Questions - Word Problems

The following questions involve using Pythagoras' theorem to solve a range of word problems involving 'real-life' type questions.

On the first sheet, only the hypotenuse needs to be found, given the measurements of the other sides.

Illustrations have been provided to support students solving these word problems.

• Pythagoras Theorem Word Problems 1
• Pythagoras Theorem Word Problems 2

Geometry Formulas

• Geometry Formula Sheet

Here you will find a support page packed with a range of geometric formula.

Included in this page are formula for:

• areas and volumes of 2d and 3d shapes
• interior angles of polygons
• angles of 2d shapes
• triangle formulas and theorems

This page will provide a useful reference for anyone needing a geometric formula.

Triangle Formulas

Here you will find a support page to help you understand some of the special features that triangles have, particularly right triangles.

Using this support page will help you to:

• understand the different types and properties of triangles;
• understand how to find the area of a triangle;
• know and use Pythagoras' Theorem.

All the free printable geometry worksheets in this section support the Elementary Math Benchmarks.

• Geometry Formulas Triangles

Here you will find a range of geometry cheat sheets to help you answer a range of geometry questions.

The sheets contain information about angles, types and properties of 2d and 3d shapes, and also common formulas associated with 2d and 3d shapes.

Included in this page are:

• images of common 2d and 3d shapes;
• properties of 2d and 3d shapes;
• formulas involving 2d shapes, such as area and perimeter, pythagoras' theorem, trigonometry laws, etc;
• formulas involving 3d shapes about volume and surface area.

Using the sheets in this section will help you understand and answer a range of geometry questions.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to Geometry Section

Return from Pythagoras Theorem Questions to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

15 Pythagorean Theorem Practice Problems For 8th Grade

Beki Christian

Pythagorean Theorem practice problems involve using the relationship between the sides of a right triangle to calculate missing side lengths in triangles. The Pythagorean Theorem is introduced in 8th grade and is used to solve a variety of problems across high school.

Here, you’ll find a selection of Pythagorean Theorem questions that demonstrate the different types of questions students are likely to encounter in 8th grade.

What is the Pythagorean Theorem?

The Pythagorean Theorem is the geometric theorem that states that the square of the hypotenuse (longest side) of a right triangle is equal to the sum of the squares of the two shorter sides of the triangle.

This can be written as a^2+b^2=c^2 for a triangle labeled like this:

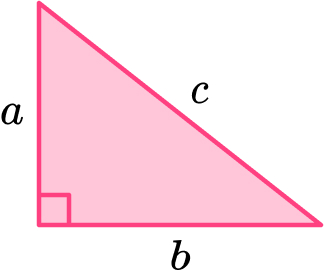
15 Pythagoras Theorem Practice Problems

Find all of the Pythagoras Theorem questions included in this blog in this easy to download resource. Suitable for 8th grade students. Includes answer key.

How to answer Pythagorean Theorem questions

1 – Label the sides of the triangle a , b , and c . Note that the hypotenuse, the longest side of a right triangle, is opposite the right angle and will always be labeled .

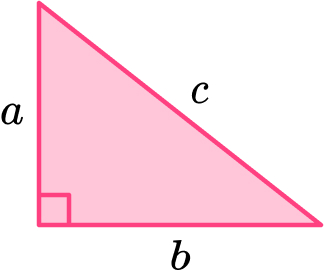
2 – Write down the formula and substitute the values>

3 – Calculate the answer. You may be asked to give your answer in an exact form or round to a given degree of accuracy, such as a certain number of decimal places or significant figures.

Pythagorean Theorem in real life

Pythagorean Theorem has many real-life uses, including in architecture and construction, navigation and surveying.

Pythagorean Theorem in 8th grade

Pythagorean Theorem is usually introduced in middle school, as it is a part of the 8th grade Common Core Math Standards.

The emphasis in middle school is on students being able to:

• Explain the Pythagorean Theorem;
• Use the theorem to solve mathematical and real-world problems – with both 2D and 3D figures;
• Use the theorem to calculate the distance between two points on a coordinate grid.

The process for solving any Pythagoras Theorem problem always begins by identifying the relevant right-angled triangle and labeling the sides a , b , c. If there is not a diagram in the question, it can be helpful to draw one.

Where necessary, round your answers to 3 significant figures.

Pythagorean Theorem practice problems

1. A ship sails 6 \, km East and then 8 \, km North. Find the ship’s distance from its starting point.

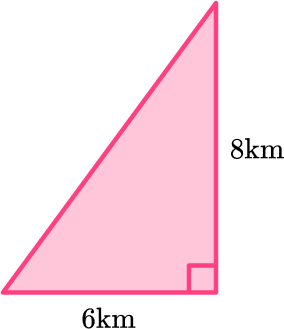
The ship is 10 kilometers from its starting point.

2. A ladder is 5 \, m long. The base of the ladder is 3 \, m from the base of a vertical wall. How far up the wall does the ladder reach?

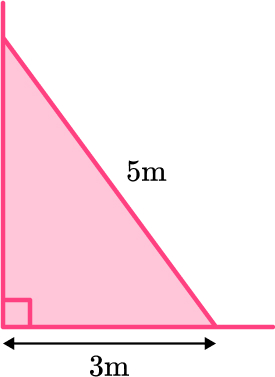
The ladder reaches 4 meters up the wall.

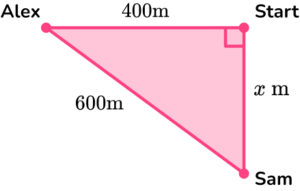
3. Alex and Sam start from the same point. Alex walks 400 meters west. Sam walks x meters south, until they are 600 \, m apart from each other. How far does Sam walk?

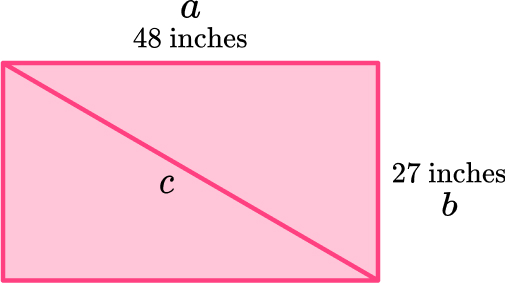
4. A television’s size is the measurement from the upper left hand corner of the television to the bottom right hand corner. Find the size of this television.

39.7 inches

55.1 inches

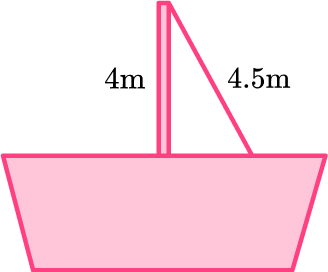
5. The pole of a sailing boat is supported by a rope from the top of the pole to an anchor point on the deck. The pole is 4 \, m long and the rope is 4.5 \, m long. Calculate the distance from the base of the pole to the anchor point of the rope on the deck.

6. Work out the length of the diagonal of a square with 8 \, cm sides.

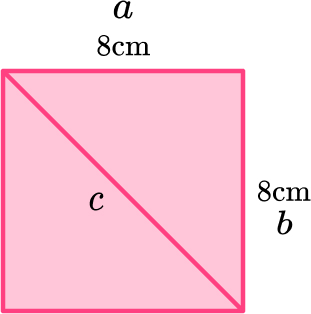
The diagonal of the square has a length of 11.3 centimeters.

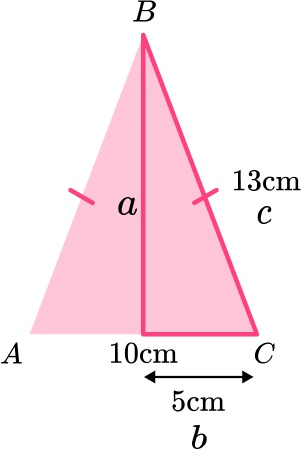
7. ABC is an isosceles triangle.

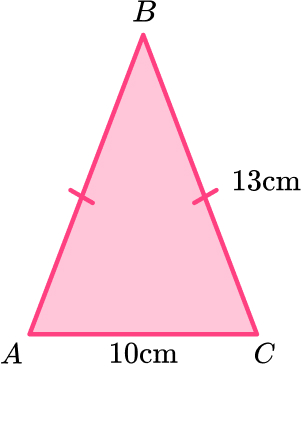
Work out the height of the triangle.

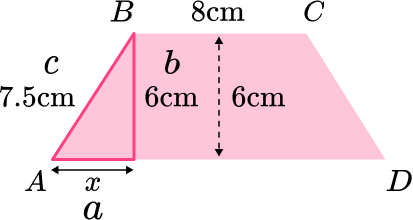
8. ABCD is an isosceles trapezoid.

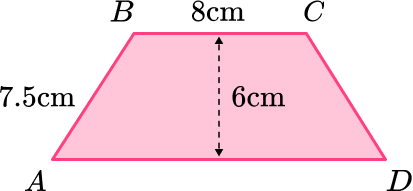
Work out the length of AD.

9. Here is a cm square grid. Calculate the distance between the points A and B.

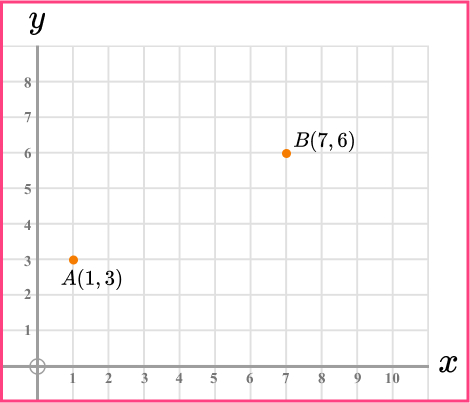
10. Which is a right angled triangle?

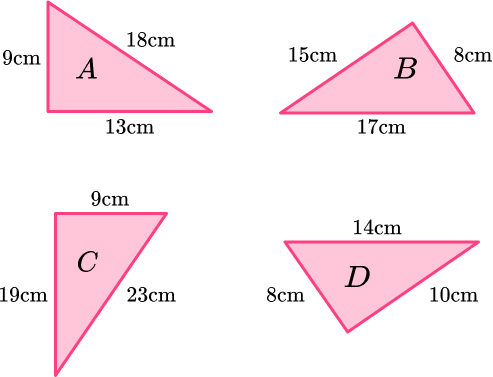
Not a right angled triangle because Pythagorean Theorem doesn’t work.

Right angled triangle because Pythagorean Theorem works.

11. PQRS is made from two right angled triangles.

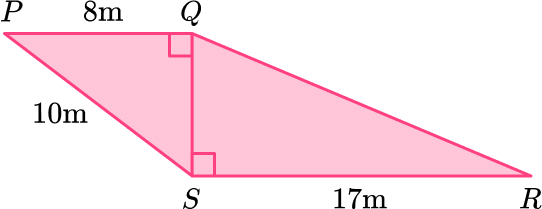
Work out the length of QR.

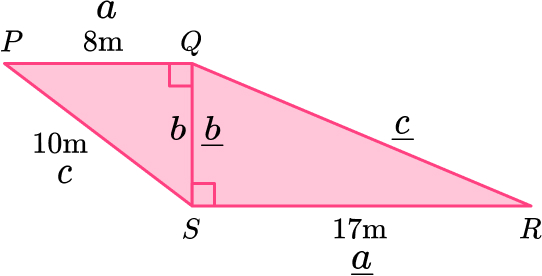
Triangle \text{PQS:}

Triangle \text{QRS}

12. Here is a pattern made from right angled triangles. Work out the length x.

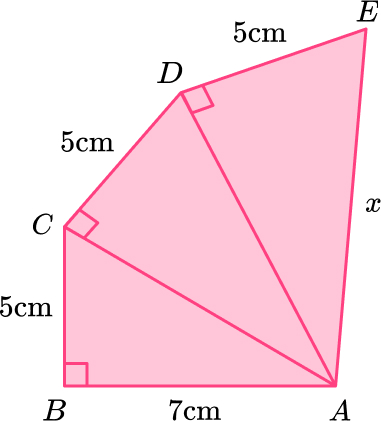
Triangle \text{ABC:}

Triangle \text{ACD:}

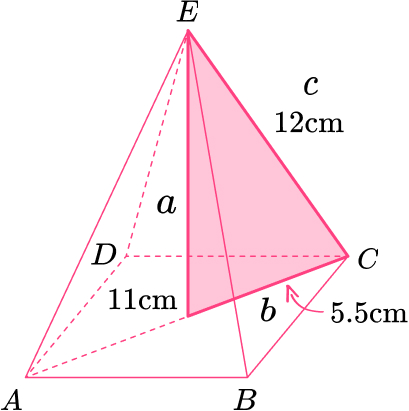
13. Here is a pyramid.

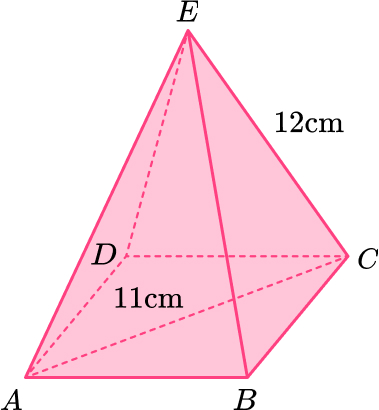
Work out the height of the pyramid.

14. Here is a cuboid.

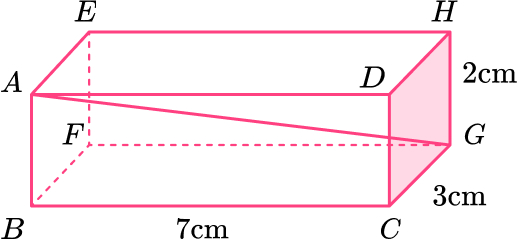
Work out the length AG.

Give your answer in its exact form.

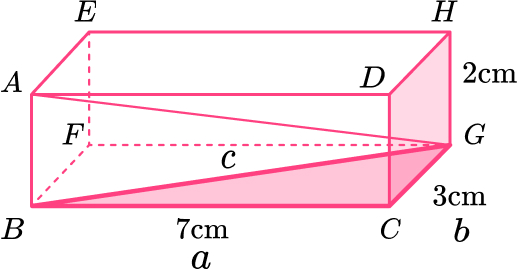
Length of \text{BG:}

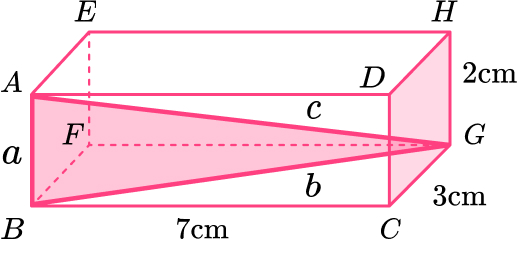
Length of \text{AG:}

15. Here is a right angled triangle.

Form an equation and use it to work out the value of x.

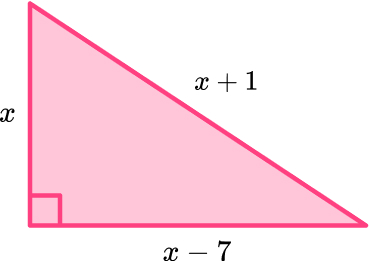
x=4 \, or \, x=12

x cannot be 4 as you can’t have a negative side length so x=12

Pythagorean Theorem in middle school

In middle school, students…

• prove the Pythagorean Theorem;
• use the Pythagorean Theorem with trigonometric ratios to solve problems;
• use the Pythagorean Theorem in proofs.

Pythagoras Theorem may feature in questions alongside other topics, such as trigonometry, circle theorems or algebra.

The Pythagorean Theorem is used to calculate a missing length in a right triangle . If you have a right angled triangle and you know two of the lengths, label the sides of the triangle a,b and c (c must be the hypotenuse – the longest side). Pythagorean Theorem is a^2+b^2=c^2. Substitute the values you know into Pythagorean Theorem and solve to find the missing side.

The hypotenuse of a right triangle is the longest side. If you know the lengths of the other two sides, you can find the length of the hypotenuse by squaring the two shorter sides, adding those values together and then taking the square root. By doing this you are finding c in a^2+b^2=c^2

If your triangle is a right triangle and you know two of the sides, you can use Pythagorean Theorem to find the length of the third side. To do this, label the sides a , b and c (with c being the hypotenuse – the longest side). Substitute the values you know into a^2+b^2=c^2 and solve to find the missing side.

Looking for more Pythagorean theorem math questions?

• Ratio questions
• Algebra questions
• Probability questions
• Trigonometry questions
• Venn diagram questions
• Long division questions

RELATED RESOURCE :

• 6th Grade Math Problems
• 7th Grade Math Problems
• 8th grade math problems

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by former UK Secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary and middle school teacher Kathleen Epperson.

Related articles

36 Math Problems For 1st Graders With Answers & Teaching Ideas

30 8th Grade Math Problems: Answers With Worked Examples

28 Math Problems For 2nd Graders With Answers & Teaching Ideas

37 Math Problems For 3rd Graders: Answers With Worked Examples

3rd to 8th Grade Practice Tests

Get ready for your state math test with our 3rd to 8th grade practice assessments. These 6 multiple-choice tests, created by US math experts, cover essential topics and include detailed answers for effective test prep. Aligned with Common Core Standards, they’re the perfect tool to build student confidence.

Privacy Overview

Pythagoras Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2025

• Maths Questions

Pythagoras Theorem Questions

Pythagoras theorem questions with detailed solutions are given for students to practice and understand the concept. Practising these questions will be a plus point in preparation for examinations. Let us discuss in brief about the Pythagoras theorem.

Pythagoras’ theorem is all about the relation between sides of a right-angled triangle. According to the theorem, the hypotenuse square equals the sum of squares of the perpendicular sides.

Click here to learn the proof of Pythagoras’ Theorem .

Video Lesson on Pythagoras Theorem

Pythagoras Theorem Questions with Solutions

Now that we have learnt about the Pythagoras Theorem, lets apply the same by solving the following questions.

Question 1: In a right-angled triangle, the measures of the perpendicular sides are 6 cm and 11 cm. Find the length of the third side.

Let ΔABC be the triangle, right-angled at B, such that AB and BC are the perpendicular sides. Let AB = 6 cm and BC = 11 cm

Then, by the Pythagoras theorem,

AC 2 = AB 2 + BC 2

\(\begin{array}{l}\Rightarrow AC=\sqrt{(AB^{2}+BC^{2})}=\sqrt{6^{2}+11^{2}}\end{array} \)

\(\begin{array}{l}=\sqrt{36+121}=\sqrt{157}\end{array} \)

∴ AC = √157 cm.

Question 2: A triangle is given whose sides are of length 21 cm, 20 cm and 29 cm. Check whether these are the sides of a right-angled triangle.

If these are the sides of a right-angled triangle, it must satisfy the Pythagoras theorem.

We have to check whether 21 2 + 20 2 = 29 2

Now, 21 2 + 20 2 = 441 + 400 = 841 = 29 2

Thus, the given triangle is a right-angled triangle.

Question 3: Find the Pythagorean triplet with whose one number is 6.

Now, m 2 + 1 = 9 + 1 = 10

and m 2 – 1 = 9 – 1 = 8

Therefore, the Pythagorean triplet is (6, 8, 10).

Question 4: The length of the diagonal of a square is 6 cm. Find the sides of the square.

Let ABCD be the square, and let AC be the diagonal of length 6 cm. Then triangle ABC is the right-angled triangle such that AB = BC (∵ all sides of a square are equal)

By Pythagoras theorem,

⇒ AC 2 = 2AB 2

⇒ AC = √2 AB

⇒ AB = (1/√2) AC = (1/√2)6 = 3√2 cm.

Question 5: A ladder is kept at a distance of 15 cm from the wall such that the top of the ladder is at the height of 8 cm from the bottom of the wall. Find the length of the wall.

Let AB be the ladder of length x.

AC 2 + BC 2 = AB 2

\(\begin{array}{l}\Rightarrow AB=\sqrt{AC^{2}+BC^{2}}\end{array} \)

\(\begin{array}{l}\Rightarrow x=\sqrt{8^{2}+15^{2}}=\sqrt{64+225}\end{array} \)

⇒ x = 17 cm

∴ Length of the ladder is 17 cm.

Question 6: Find the area of a rectangle whose length is 144 cm and the length of the diagonal 145 cm.

Let the rectangle be ABCD

\(\begin{array}{l}\Rightarrow AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{145^{2}-144^{2)}\end{array} \)

⇒ AD = √(21025 – 20736) = √289

⇒ AD = 17 cm

Thus, area of the rectangle ABCD = 17 × 144 = 2448 cm 2 .

• Properties of Triangles
• Congruence of Triangles
• Similar Triangles
• Trigonometry

Question 7: A boy travels 24 km towards east from his house, then he turned his left and covers another 10 km. Find out his total displacement?

Let the boy’s house is at point O, then to find the total displacement, we have to find OB.

Clearly, ΔOAB is a right-angled triangle, by Pythagoras theorem,

\(\begin{array}{l} OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{24^{2}-10^{2}}\end{array} \)

⇒ OB = √(576 + 100) = √676

⇒ OB = 26 km.

Question 8: Find the distance between a tower and a building of height 65 m and 34 m, respectively, such that the distance between their top is 29 m.

The figure below shows the situation. Let x be the distance between the tower and the building.

In right triangle DCE, by Pythagoras theorem,

CE = √(DE 2 – DC 2 ) = √(29 2 – 21 2 )

⇒ x = √(841 – 441) = √400

⇒ x = 20 m.

∴ the distance between the tower and the building is 20 m.

Question 9: Find the area of the triangle formed by the chord of length 10 cm of the circle whose radius is 13 cm.

Let AB be the chord of the circle with the centre at O such that AB = 10 and OA = OB = 13. Draw a perpendicular OM on AB.

By the property of circle, perpendicular dropped from the centre of the circle on a chord, bisects the chord.

Then, AM = MB = 5 cm.

Now, in right triangle OMB,

OB 2 = OM 2 + MB 2

⇒ OM = √(OB 2 – MB 2 )

⇒ OM = √(13 2 – 5 2 ) = √(169 – 25)

⇒ OM = √144 = 12 cm

Area of triangle OAB = ½ × AB × OM

= ½ × 10 × 12

= 60 cm 2 .

Question 10: Find the length of tangent PT where P is a point which is at a distance 10 cm from the centre O of the circle of radius 6 cm.

Given, OP = 10 cm and OT = 6m.

We have to find the value of PT.

By the property of tangents, the radius of the circle is perpendicular to the tangent at the point of contact.

Thus, triangle OTP is a right-angled triangle.

∴ by the Pythagoras theorem,

OP 2 = OT 2. + PT 2

⇒ PT = √(OP 2 – OT 2 ) = √(10 2 – 6 2 )

⇒ PT = √(100 – 36) = √64

⇒ PT = 8 cm.

Related Video on Pythagorean Triples

Practice Questions on Pythagoras Theorem

1. Find the area of a right-angled triangle whose hypotenuse is 13 cm and one of the perpendicular sides is 5 cm.

2. Find the Pythagorean triplet whose one member is 15.

3. Find the perimeter of a rectangle whose diagonal is 5 cm and one of its sides is 4 cm.

4 if a pole of length 65 cm is kept leaning against a wall such that the pole reaches up to a height of 63 cm on the wall from the ground. Find the distance between the pole and the wall.

5. Find the area of the triangle inscribed within a circle of radius 8.5 cm such that one of the sides of the triangle is the diameter of the circle and the length of the other side is 8 cm.

(Hint: The triangle is formed in semi-circular region and angle of a semi-circle is of 90 o )

Learn about various mathematical concepts in a simple manner with detailed information, along with step by step solutions to all questions, only at BYJU’S. Download BYJU’S – The Learning App to get personalised videos.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Pythagorean Theorem Worksheets

Free Pythagorean Theorem Worksheets with Answer Keys

Looking for a free Pythagorean Theorem worksheet for extra math practice?

Are you in need of some Pythagorean Theorem worksheets to help you practice and learn one of the most famous math theorems ever known?

Learning how to correctly use the Pythagorean Theorem, which states that, for any right triangle with sides a, b, and c (where a and b are the legs and c is the hypotenuse), the following equation is always true: a² + b² = c².

The Pythagorean Theorem has been around for thousands of years and it remains as one of the most fascinating and well-known math theorems of all time. Learning how to use the Pythagorean Theorem to solve problems involving right triangles is a skill that every math student can learn with some consistent practice. And one of the best ways to consistently practice using the Pythagorean Theorem to solve right triangle problems is by working on a Pythagorean Theorem Worksheet or two assess your understanding and to keep your skills sharp!

If you are looking for effective Pythagorean Theorem Worksheets (that include both triangle diagram problems and word problems), then you’re in the right place! The next section of this page shares a free library of Pythagorean Theorem Worksheet PDF files that include a variety of practice problems as well as complete answer keys on the second page. These free worksheets will give you tons of practice opportunities to use the Pythagorean Theorem (a² + b² = c²) to solve a variety of right triangle problems (including word problems).

Every single Pythagorean Theorem worksheet pdf file is easy to download to your computer and/or print (with or without the answer key). You can download any of the worksheets in the free library below simply by clicking on any of the blue text links to open the PDF preview. From the preview page, you will have the option to save the file to your computer or to send it to your printer if you want a paper version of any of the worksheets.

All of the Pythagorean Theorem Worksheets below are samples from the Mashup Math K-12 Infinite Worksheet Libraries , where you can find hundreds more topic-specific math worksheets with answer keys for grades K-9, Algebra I, and Geometry.

Pythagorean Theorem Worksheet (A)

Click Image to Preview

▶️ Practice with the Pythagorean Theorem (A)

▶️ Practice with the Pythagorean Theorem (B)

▶️ Practice with the Pythagorean Theorem (C)

▶️ Practice with the Pythagorean Theorem (D)

▶️ Practice with the Pythagorean Theorem (E)

Pythagorean Theorem Worksheet (B)

▶️ Pythagorean Theorem word problems (A)

▶️ Pythagorean Theorem word problems (B)

▶️ Pythagorean Theorem word problems (C)

Pythagorean Theorem Worksheet (C)

▶️ Practice with square roots (A)

▶️ Practice with square roots (B)

▶️ Practice with square roots (C)

▶️ Solving Radical Equations (A)

▶️ Solving Radical Equations (B)

🛑 HOLD ON! Do YOU Want More Topic-Specific Worksheets for Grades K-12+? 🙋‍♀️

If so, please visit our Free Math Worksheets Library , where you can download hundreds of PDF math worksheets and answer keys for Grades K-9, Algebra I, and Geometry!

Quick Review: The Pythagorean Theorem

If you are struggling with any of the practice problems on any Pythagorean Theorem worksheet above, here is a short review of some key concepts related to the Pythagorean Theorem.

First, note that the Pythagorean Theorem applies only to right triangles. If a math problem is related to a triangle that does not have a 90-degree angle, then you likely can not use the Pythagorean Theorem to solve it.

However, in the case of all right triangles with the following properties:

The legs of the right triangle (the two smaller sides) are a and b

The hypotenuse of the right triangle (the longest side) is c

Then the following is always true: a² + b² = c²

In other words, the square of the length of the longest side, c, is equal to the sum of the squares of the two smaller sides, a and b.

To help you to visualize how the Pythagorean Theorem relates to a right triangle with side lengths a, b, and c (where c is the hypotenuse), take a look at Figure 01 below.

Figure 01: Pythagorean Theorem Worksheet: a² + b² = c²

For example, let’s say that you have a triangle with side lengths 3, 4, and 5, and you wanted to confirm whether or not the triangle in question was a right triangle.

To verify whether or not the triangle is right, we would have to substitute the three side lengths into the Pythagorean Theorem, a² + b² = c², and see if the equation holds true. If it does, then we can conclude that the triangle is a right triangle.

In this case, the shorter sides a and b are 3 and 4, and the longest side is 5, so:

Next, we just have to plug these values into the Pythagorean Theorem as follows:

a² + b² = c²

3² + 4² = 5²

9 + 16 = 25

What do you notice? The left side of the equation, 3² + 4² = 9 + 16 = 25, and the right side of the equation, 5² = 25, both equal 25. So, we can conclude that this triangle is a right triangle because it satisfies the Pythagorean Theorem, as illustrated in Figure 02 below.

Figure 02: Pythagorean Theorem Worksheet Practice Problem: Use the Pythagorean Theorem to prove that a triangle with side lengths 3, 4, and 5 is a right triangle.

If you or your students need a more in-depth review of how to use the Pythagorean Theorem to find the missing side of a right triangle, check out our free video tutorial linked below!

Get More Free Math Resources!

Sign up for our mailing list and get two free pdf workbooks!

Pythagoras Theorem Questions (with Answers)

Pythagoras theorem.

In a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.

• Length of the hypotenuse is c
• The hypotenuse is the longest side
• Lengths of the other sides are a, b

Right Triangle Questions – using the theorem

The Theorem helps us in:

• Finding Sides: If two sides are known, we can find the third side.
• Determining if a triangle is right-angled: If the sides of a triangle are known and satisfy the Pythagoras Formula, it is a right-angled triangle.

There is a proof of this theorem by a US president. Its simplicity makes it is easy enough for the grade 8 kids to understand.

Finding the missing sides (side lengths) of a Right Triangle

The theorem gives a relation among the three sides of a right-angled triangle. We can find one side if we know the other two sides. How?

Example: We are given (see figure) below the two sides of the right triangle. Find the third side.

Given: a = 3, c = 5

Which side is the hypotenuse?

✩ Always identify the hypotenuse first

Unknown side = BC = b ?

Putting the values in the Pythagoras Formula: a 2 + b 2 = c 2

3 2 + b 2 = 5 2

9 + b 2 = 25

b 2 = 25 − 9 = 16 = 4 2

Finding the Hypotenuse of a Triangle

Using the Pythagoras formula, finding hypotenuse is no different from any other side.

Example: Sides of a right triangle are 20 cm and 21 cm, find its hypotenuse.

Pythagoras Formula: a 2 + b 2 = c 2

• c is the length of the hypotenuse
• a, b are the lengths of the other two sides (you can assume any length as a or b ).

Let AB = a = 20, BC = b = 21

Putting values in the formula:

20 2 + 21 2 = c 2

400 + 441 = c 2

Finding Right Triangle

Given the sides, we can determine if a triangle is right-angled by applying the Pythagoras Formula. How?

• Assume the longest side to be hypotenuse Length = c . Find its square ( = c 2 )
• Find the sum of squares of the other two sides ( = a 2 + b 2 )
• If a 2 + b 2 ≠ c 2 it is a not right triangle
• If a 2 + b 2 = c 2 it is a right triangle

Example: A triangle has sides 8 cm, 11 cm, and 15 cm. Determine if it is a right triangle

Longest side = 15 cm. Let us assume it to be hypotenuse = c (as we know that it is always the longest)

c 2 = 15 2 = 225

Other sides a = 8 cm b = 11 cm. (You can assume any side length to be a or b ).

a 2 + b 2 = 8 2 + 11 2 = 64 + 121 = 185

a 2 + b 2 ≠ c 2

So this is not a right-angled triangle.

Example: The sides of a triangle are 8 cm, 17 cm, and 15 cm. Find if it is a right triangle.

Longest side = 17 cm. Let us assume it to be hypotenuse = c

c 2 = 17 2 = 289

Other sides a = 8 cm, b = 15 cm.

a 2 + b 2 = 8 2 + 15 2 = 64 + 225 = 289

So a 2 + b 2 = c 2

It is a right-angled triangle.

Pythagoras Questions Types

You will encounter the following types of questions related to this theorem:

• Find a side, given two sides These questions are the direct application of the theorem (formula) and are easiest to solve.
• Express the relation between the two sides in an equation
• Substitute one side by the other using the first equation in the Pythagoras Formula
• Given the Perimeter and one side, find other sides – Perimeter is the sum of the three sides. Since one side is known, we subtract it from the perimeter to get a relationship between the other two sides.
• Given Area and one side find other sides – Area = 2 1 ​ × ( ba se × a lt i t u d e ) . Base and altitude can be the sides with the right angle OR the hypotenuse and the altitude.

Pythagoras Questions

The questions chosen have minimal use of other concepts, yet, some of these are hard Pythagoras questions (See Ques 4 and Ques 10 ).

1 Question

ABC is a right triangle. AC is its hypotenuse. Length of side AB is 2√5 . Side BC is twice of side AB. Find the length of AC.

Can you express BC in terms of AB and apply the Pythagoras Theorem?

Ans.   AC = 10

2 Question

The hypotenuse of a right triangle is 6 cm . Its area is 9 cm 2 . Find its sides.

Can you form two equations – one using area and the other using the Pythagoras formula?

Ans.   Each side is 3√2 cm.

3 Question

One side of a right triangle is 4 10 ​ cm. Find the length of its other side if the hypotenuse is 13 cm.

Can you directly apply the Pythagoras Theorem?

Ans.   3 cm

4 Question

In a right triangle ABC, length of the medians to the sides AB and BC are 2 61 ​ and 601 ​ respectively. Find the length of its hypotenuse.

CE = 2 61 ​

Let AE = EB = x

BD = DC = y

Can you use the Pythagorean Theorem to form an equation between x, y, and AD?

Can you form another equation involving x, y, and EC?

Can you use this result to find A C 2 ? Use the triangle ABC.

Ans.   AC = 26

5 Question

In a right triangle, the longest side is 8 cm. One of the remaining sides is 4√3 cm long. Find the length of the other side.

Can you apply the Pythagoras Theorem directly?

Ans.   4 cm

6 Question

The first side of a right triangle is shorter than the second side by 1 cm. It is longer than the third side by 31 cm. Find the sides of the triangle.

Can you form equations between the first side and the other two sides? Which side is the hypotenuse?

Ans.   9 cm, 40 cm, 41 cm

7 Question

The perimeter of a right triangle is equal to 30 cm. The length of one of its sides is 10 cm. Find its hypotenuse.

Can you find the relation between the unknown side and the perimeter in terms of the hypotenuse?

Ans.   12.5 cm

8 Question

The sides of a triangle are 5 cm, 9 cm, and 12 cm. Is it a right-angled triangle?

Can you identify the possible hypotenuse? Also, test if the sides satisfy the Pythagoras Formula.

Ans.   Not a right triangle.

9 Question

In a right triangle, two sides are equal. The longest side is 7√2 cm, find the remaining sides.

Ans.   7 cm

10 Question

In the following right triangle altitude BD = 9 10 ​ cm and DC = 27 10 ​ cm. Find the sides of the triangle.

Can you apply the Pythagoras Theorem to the triangle BCD?

Can you form an equation between a and x using the triangle ABD?

Can you find the value of x using above equations and triangle ABC?

Ans.   AB = 30cm, BC = 90cm, A C = 30 10 ​ c m

Answers to Pythagoras Questions

1 answer.

Let AB = a , BC = b and AC = c .

AB = a = 2√5

BC is twice of AB, b = 2a = 4√5

AC = Hypotenuse = c

Applying the Pythagoras Theorem a 2 + b 2 = c 2 :

(2√5) 2 + (4√5) 2 = c 2

4(5) + 16(5) = c 2

c 2 = 20 + 80 = 100

2 Answer

Let AB = a , BC = b

In triangle ABC, base = b and altitude = a

Area of Triangle = 2 1 ​ × ( ba se × a lt i t u d e ) . So:

2 1 ​ × ( ab ) = 9

ab = 18 (Equation 1)

Using the Pythagoras Formula:

a 2 + b 2 = 6 2 = 36

We add and subtract 2ab to complete the square :

a 2 + b 2 − 2ab + 2ab = 36

(a − b) 2 + 2ab = 36

(a − b) 2 + 36 = 36 Using ab = 18 from Equation 1

(a − b) 2 = 0

Substituting a by b in Equation 1:

Side AB = BC = 3√2 cm

3 Answer

Let the length of sides be a, b and c , such that:

a = 4 10 ​ cm

b = unknown

From the Pythagoras formula a 2 + b 2 = c 2 , we get:

( 4 10 ​ ) 2 + b 2 = 1 3 2

(16 × 10) + b 2 = 169

160 + b 2 = 169

b 2 = 169 − 160 = 9

4 Answer

Using triangle ABD:

AB 2 + BD 2 = AD 2

( 2 x ) 2 + y 2 = ( 601 ​ ) 2

4 x 2 + y 2 = 601 (Equation 1)

Using triangle EBC :

EB 2 + BC 2 = EC 2

x 2 + ( 2 y ) 2 = ( 2 61 ​ ) 2

x 2 + 4 y 2 = ( 2 61 ​ ) 2

x 2 + 4 y 2 = 244 (Equation 2)

Adding Equation 1 and 2:

4x 2 + y 2 + x 2 + 4y 2 = 601 + 244

5x 2 + 5y 2 = 845

x 2 + y 2 = 169 (Equation 3)

Let us solve for the hypotenuse using the triangle ABC:

AB 2 + BC 2 = AC 2

(2x) 2 + (2y) 2 = AC 2

4x 2 + 4y 2 = AC 2

4(x 2 + y 2 ) = AC 2

Substituting the value of x 2 + y 2 from Equation 3:

4(169) = AC 2

A C = 4 ( 169 ) ​

AC = 2 × 13 = 26

5 Answer

Let the lengths of sides be a, b and c (hypotenuse).

Hypotenuse is the longest side. So c = 8 .

Let b = 4√3 .

From the Pythagoras Theorem:

a 2 + b 2 = c 2

a 2 + (4√3) 2 = 8 2

a 2 + 16(3) = 64

a 2 + 48 = 64

The third side is 4 cm.

6 Answer

The second side is the longest. It is the hypotenuse. Let its length be c .

Let the length of first side be b and third side a .

Applying the Pythagoras formula:

(b − 31) 2 + b 2 = (b + 1) 2

b 2 − 62b + 31 2 + b 2 = b 2 + 2b + 1

b 2 − 62b + 961 = 2b + 1

b 2 − 64b + 960 = 0

b 2 − 24b − 40b + 960 = 0

b(b − 24) − 40(b − 24) = 0

(b − 40)(b − 24) = 0

b = 40 Or b = 24

For b = 24 , we get a = 24 − 31 = − 7 . Length of a side cannot be negative, so we reject b = 24 .

For b = 40 , we get a = 40 − 31 = 9 and c = 40 + 1 = 41

The sides of triangle are 9 cm, 40 cm and 41 cm.

7 Answer

Side BC = b = 10 cm

Perimeter = Sum of the sides

= a + b + c = 30 (Given)

a + 10 + c = 30

a = 20 − c ( Equation 1 )

Applying the Pythagoras Theorem to find the hypotenuse:

Using Equation 1 to substitute the value of a

(20 − c) 2 + (10) 2 = c 2

400 − 40c + c 2 + 100 = c 2

500 − 40c = 0

The length of hypotenuse = 12.5 cm

8 Answer

Longest side = 12 cm. Let us assume it to be the hypotenuse = c

So c 2 = 12 2 = 144

The Pythagoras Formula: a 2 + b 2 = c 2

We can assume any side to be a or b.

Let a = 5 cm, b = 9 cm.

a 2 + b 2 = 5 2 + 9 2 = 25 + 81 = 106

So a 2 + b 2 ≠ c 2

This is a not a right angled triangle.

9 Answer

Let the length of the sides be a, b , and c (hypotenuse).

In a right triangle hypotenuse is the longest side. So c = 7√2

Other sides are equal. So a = b .

Applying the Pythagoras theorem:

b 2 + b 2 = (7√2) 2

2b 2 = 49(2)

Each side is 7 cm.

10 Answer

Let AB = a, BC = b, AC = c and AD = x

Given B D = 9 10 ​ D C = 27 10 ​

Applying Pythagoras Theorem to triangle BCD:

BD 2 + DC 2 = BC 2

( 9 10 ​ ) 2 + ( 27 10 ​ ) 2 = B C 2

(9 2 × 10) + (27 2 × 10) = b 2

810 + 7290 = b 2

Applying Pythagoras Theorem to triangle ABD:

BD 2 + AD 2 = AB 2

a 2 = ( 9 10 ​ ) 2 + x 2 (Equation 1)

From the figure:

AC = AD + BD

c = x + 27 10 ​ (Equation 2)

Applying Pythagoras Theorem to triangle ABC:

Using b = 90 and value of a 2 from Equation 1 and c from Equation 2:

( 9 10 ​ ) 2 + x 2 + 9 0 2 = ( x + 27 10 ​ ) 2

9 2 ( 10 ) + x 2 + 9 0 2 = x 2 + 54 10 ​ x + 2 7 2 ( 10 )

810 + 8100 = 54 10 ​ x + 7290

54 10 ​ x = 8910 − 7290 = 1620

x = 10 ​ 30 ​

Putting value of x in Equation 1:

a 2 = ( 9 10 ​ ) 2 + ( 3 10 ​ ) 2

a 2 = 810 + 90 = 900

Using value of a and b in Pythagoras Formula for triangle ABC:

30 2 + 90 2 = c 2

900 + 8100 = c 2

c = 30 10 ​

AB = 30cm, BC = 90cm, A C = 30 10 ​ c m

Difficult Pythagoras Questions (Year 10, Guided Answers) ➤

James Garfield Pythagorean Theorem (Illustration & Proof) ➤