multiple linear regression and hypothesis testing

Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .

• Payment Plans
• Product List
• Partnerships

• Try Free Trial
• Study Packages
• Levels I, II & III Lifetime Package
• Video Lessons
• Study Notes
• Practice Questions
• Levels II & III Lifetime Package
• About the Exam
• About your Instructor
• Part I Study Packages
• Parts I & II Packages
• Part I & Part II Lifetime Package
• Part II Study Packages
• Exams P & FM Lifetime Package
• Quantitative Questions
• Verbal Questions
• Data Insight Questions
• Live Tutoring
• About your Instructors
• EA Practice Questions
• Data Sufficiency Questions
• Integrated Reasoning Questions

Hypothesis Tests and Confidence Intervals in Multiple Regression

After completing this reading you should be able to:

• Construct, apply, and interpret hypothesis tests and confidence intervals for a single coefficient in a multiple regression.
• Construct, apply, and interpret joint hypothesis tests and confidence intervals for multiple coefficients in a multiple regression.
• Interpret the \(F\)-statistic.
• Interpret tests of a single restriction involving multiple coefficients.
• Interpret confidence sets for multiple coefficients.
• Identify examples of omitted variable bias in multiple regressions.
• Interpret the \({ R }^{ 2 }\) and adjusted \({ R }^{ 2 }\) in a multiple regression.

Hypothesis Tests and Confidence Intervals for a Single Coefficient

This section is about the calculation of the standard error, hypotheses testing, and confidence interval construction for a single regression in a multiple regression equation.

Introduction

In a previous chapter, we looked at simple linear regression where we deal with just one regressor (independent variable). The response (dependent variable) is assumed to be affected by just one independent variable.  M ultiple regression, on the other hand ,  simultaneously considers the influence of multiple explanatory variables on a response variable Y. We may want to establish the confidence interval of one of the independent variables. We may want to evaluate whether any particular independent variable has a significant effect on the dependent variable. Finally, We may also want to establish whether the independent variables as a group have a significant effect on the dependent variable. In this chapter, we delve into ways all this can be achieved.

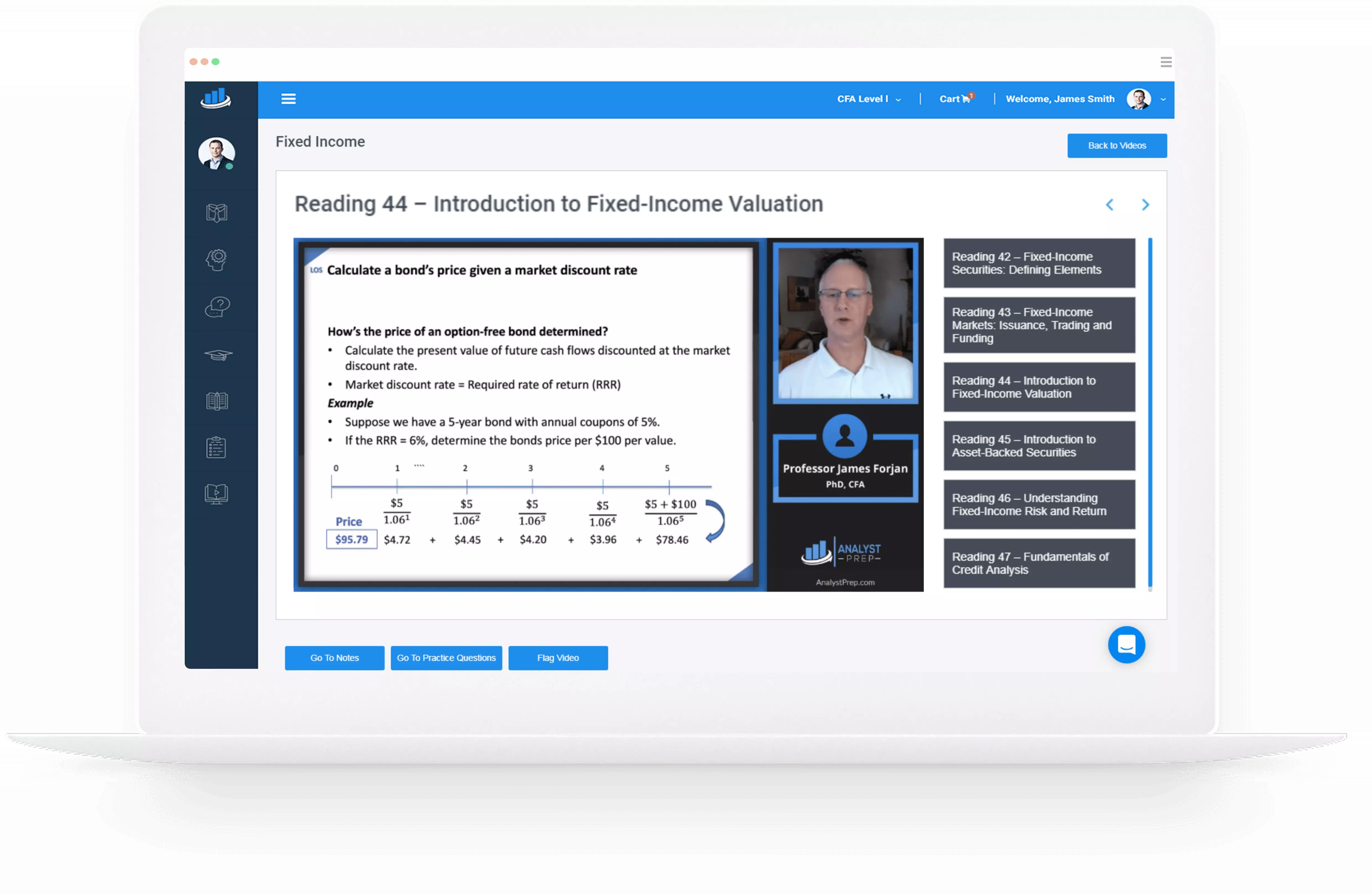
Hypothesis Tests for a single coefficient

Suppose that we are testing the hypothesis that the true coefficient \({ \beta }_{ j }\) on the \(j\)th regressor takes on some specific value \({ \beta }_{ j,0 }\). Let the alternative hypothesis be two-sided. Therefore, the following is the mathematical expression of the two hypotheses:

$$ { H }_{ 0 }:{ \beta }_{ j }={ \beta }_{ j,0 }\quad vs.\quad { H }_{ 1 }:{ \beta }_{ j }\neq { \beta }_{ j,0 } $$

This expression represents the two-sided alternative. The following are the steps to follow while testing the null hypothesis:

• Computing the coefficient’s standard error.

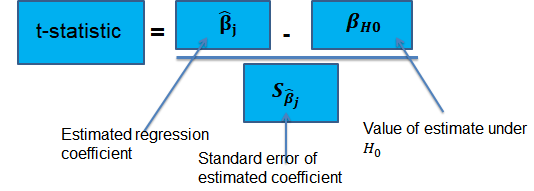
$$ p-value=2\Phi \left( -|{ t }^{ act }| \right) $$

• Also, the \(t\)-statistic can be compared to the critical value corresponding to the significance level that is desired for the test.

Confidence Intervals for a Single Coefficient

The confidence interval for a regression coefficient in multiple regression is calculated and interpreted the same way as it is in simple linear regression. 

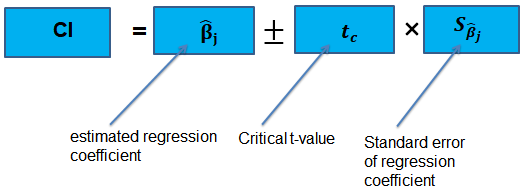
The t-statistic has n – k – 1 degrees of freedom where k = number of independents

Supposing that an interval contains the true value of \({ \beta }_{ j }\) with a probability of 95%. This is simply the 95% two-sided confidence interval for \({ \beta }_{ j }\). The implication here is that the true value of \({ \beta }_{ j }\) is contained in 95% of all possible randomly drawn variables.

Alternatively, the 95% two-sided confidence interval for \({ \beta }_{ j }\) is the set of values that are impossible to reject when a two-sided hypothesis test of 5% is applied. Therefore, with a large sample size:

$$ 95\%\quad confidence\quad interval\quad for\quad { \beta }_{ j }=\left[ { \hat { \beta } }_{ j }-1.96SE\left( { \hat { \beta } }_{ j } \right) ,{ \hat { \beta } }_{ j }+1.96SE\left( { \hat { \beta } }_{ j } \right) \right] $$

Tests of Joint Hypotheses

In this section, we consider the formulation of the joint hypotheses on multiple regression coefficients. We will further study the application of an \(F\)-statistic in their testing.

Hypotheses Testing on Two or More Coefficients

Joint null hypothesis.

In multiple regression, we canno t test the null hypothesis that all slope coefficients are equal 0 based on t -tests that each individual slope coefficient equals 0. Why? individual t-tests do not account for the effects of interactions among the independent variables.

For this reason, we conduct the F-test which uses the F-statistic .  The F-test tests the null hypothesis that all of the slope coefficients in the multiple regression model are jointly equal to 0, .i.e.,

\(F\)-Statistic

The F-statistic, which is always a one-tailed test , is calculated as:

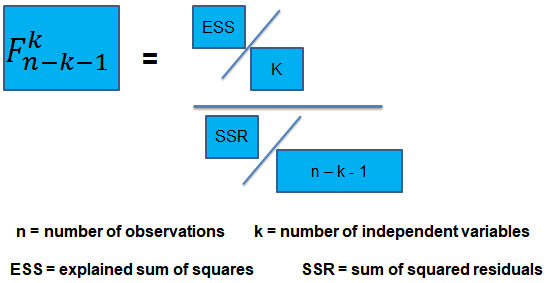
To determine whether at least one of the coefficients is statistically significant, the calculated F-statistic is compared with the one-tailed critical F-value, at the appropriate level of significance.

Decision rule:

Rejection of the null hypothesis at a stated level of significance indicates that at least one of the coefficients is significantly different than zero, i.e, at least one of the independent variables in the regression model makes a significant contribution to the dependent variable.

An analyst runs a regression of monthly value-stock returns on four independent variables over 48 months.

The total sum of squares for the regression is 360, and the sum of squared errors is 120.

Test the null hypothesis at the 5% significance level (95% confidence) that all the four independent variables are equal to zero.

\({ H }_{ 0 }:{ \beta }_{ 1 }=0,{ \beta }_{ 2 }=0,\dots ,{ \beta }_{ 4 }=0 \)

\({ H }_{ 1 }:{ \beta }_{ j }\neq 0\) (at least one j is not equal to zero, j=1,2… k )

ESS = TSS – SSR = 360 – 120 = 240

The calculated test statistic = (ESS/k)/(SSR/(n-k-1))

=(240/4)/(120/43) = 21.5

\({ F }_{ 43 }^{ 4 }\) is approximately 2.44 at 5% significance level.

Decision: Reject H 0 .

Conclusion: at least one of the 4 independents is significantly different than zero.

Omitted Variable Bias in Multiple Regression

This is the bias in the OLS estimator arising when at least one included regressor gets collaborated with an omitted variable. The following conditions must be satisfied for an omitted variable bias to occur:

• There must be a correlation between at least one of the included regressors and the omitted variable.
• The dependent variable \(Y\) must be determined by the omitted variable.

Practical Interpretation of the \({ R }^{ 2 }\) and the adjusted \({ R }^{ 2 }\), \({ \bar { R } }^{ 2 }\)

To determine the accuracy within which the OLS regression line fits the data, we apply the coefficient of determination and the regression’s standard error . 

The coefficient of determination, represented by \({ R }^{ 2 }\), is a measure of the “goodness of fit” of the regression. It is interpreted as the percentage of variation in the dependent variable explained by the independent variables

\({ R }^{ 2 }\) is not a reliable indicator of the explanatory power of a multiple regression model.Why? \({ R }^{ 2 }\) almost always increases as new independent variables are added to the model, even if the marginal contribution of the new variable is not statistically significant. Thus, a high \({ R }^{ 2 }\) may reflect the impact of a large set of independents rather than how well the set explains the dependent.This problem is solved by the use of the adjusted \({ R }^{ 2 }\) (extensively covered in chapter 8)

The following are the factors to watch out when guarding against applying the \({ R }^{ 2 }\) or the \({ \bar { R } }^{ 2 }\):

• An added variable doesn’t have to be statistically significant just because the \({ R }^{ 2 }\) or the \({ \bar { R } }^{ 2 }\) has increased.
• It is not always true that the regressors are a true cause of the dependent variable, just because there is a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
• It is not necessary that there is no omitted variable bias just because we have a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
• It is not necessarily true that we have the most appropriate set of regressors just because we have a high \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).
• It is not necessarily true that we have an inappropriate set of regressors just because we have a low \({ R }^{ 2 }\) or \({ \bar { R } }^{ 2 }\).

An economist tests the hypothesis that GDP growth in a certain country can be explained by interest rates and inflation.

Using some 30 observations, the analyst formulates the following regression equation:

$$ GDP growth = { \hat { \beta } }_{ 0 } + { \hat { \beta } }_{ 1 } Interest+ { \hat { \beta } }_{ 2 } Inflation $$

Regression estimates are as follows:

Is the coefficient for interest rates significant at 5%?

• Since the test statistic < t-critical, we accept H 0 ; the interest rate coefficient is  not   significant at the 5% level.
• Since the test statistic > t-critical, we reject H 0 ; the interest rate coefficient is not significant at the 5% level.
• Since the test statistic > t-critical, we reject H 0 ; the interest rate coefficient is significant at the 5% level.
• Since the test statistic < t-critical, we accept H 1 ; the interest rate coefficient is significant at the 5% level.

The correct answer is  C .

We have GDP growth = 0.10 + 0.20(Int) + 0.15(Inf)

Hypothesis:

$$ { H }_{ 0 }:{ \hat { \beta } }_{ 1 } = 0 \quad vs \quad { H }_{ 1 }:{ \hat { \beta } }_{ 1 }≠0 $$

The test statistic is:

$$ t = \left( \frac { 0.20 – 0 }{ 0.05 } \right)  = 4 $$

The critical value is t (α/2, n-k-1) = t 0.025,27  = 2.052 (which can be found on the t-table).

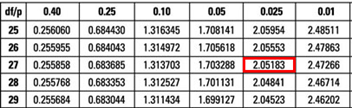
Conclusion : The interest rate coefficient is significant at the 5% level.

Offered by AnalystPrep

Modeling Cycles: MA, AR, and ARMA Models

Empirical approaches to risk metrics and hedging, trading strategies.

After completing this reading, you should be able to: Explain the motivation to... Read More

Measuring Credit Risk

After completing this reading, you should be able to: Explain the distinctions between... Read More

Machine Learning and Prediction

After completing this reading, you should be able to: Explain the role of... Read More

Risks faced by CCPs: Risks caused by C ...

After completing this reading, you should be able to: Identify and explain the... Read More

Leave a Comment Cancel reply

You must be logged in to post a comment.

Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation

Overview of this lesson.

In this lesson, we make our first (and last?!) major jump in the course. We move from the simple linear regression model with one predictor to the multiple linear regression model with two or more predictors. That is, we use the adjective "simple" to denote that our model has only predictor, and we use the adjective "multiple" to indicate that our model has at least two predictors.

In the multiple regression setting, because of the potentially large number of predictors, it is more efficient to use matrices to define the regression model and the subsequent analyses. This lesson considers some of the more important multiple regression formulas in matrix form. If you're unsure about any of this, it may be a good time to take a look at this Matrix Algebra Review .

The good news is that everything you learned about the simple linear regression model extends — with at most minor modification — to the multiple linear regression model. Think about it — you don't have to forget all of that good stuff you learned! In particular:

• The models have similar "LINE" assumptions. The only real difference is that whereas in simple linear regression we think of the distribution of errors at a fixed value of the single predictor, with multiple linear regression we have to think of the distribution of errors at a fixed set of values for all the predictors. All of the model checking procedures we learned earlier are useful in the multiple linear regression framework, although the process becomes more involved since we now have multiple predictors. We'll explore this issue further in Lesson 6.
• The use and interpretation of r 2 (which we'll denote R 2 in the context of multiple linear regression) remains the same. However, with multiple linear regression we can also make use of an "adjusted" R 2 value, which is useful for model building purposes. We'll explore this measure further in Lesson 11.
• With a minor generalization of the degrees of freedom, we use t -tests and t -intervals for the regression slope coefficients to assess whether a predictor is significantly linearly related to the response, after controlling for the effects of all the opther predictors in the model.
• With a minor generalization of the degrees of freedom, we use confidence intervals for estimating the mean response and prediction intervals for predicting an individual response. We'll explore these further in Lesson 6.

For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are:

• a hypothesis test for testing that one slope parameter is 0
• a hypothesis test for testing that all of the slope parameters are 0
• a hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0

In this lesson, we also learn how to perform each of the above three hypothesis tests.

• 5.1 - Example on IQ and Physical Characteristics
• 5.2 - Example on Underground Air Quality
• 5.3 - The Multiple Linear Regression Model
• 5.4 - A Matrix Formulation of the Multiple Regression Model
• 5.5 - Three Types of MLR Parameter Tests
• 5.6 - The General Linear F-Test
• 5.7 - MLR Parameter Tests
• 5.8 - Partial R-squared
• 5.9 - Further MLR Examples

Start Here!

• Welcome to STAT 462!
• Search Course Materials
• Lesson 1: Statistical Inference Foundations
• Lesson 2: Simple Linear Regression (SLR) Model
• Lesson 3: SLR Evaluation
• Lesson 4: SLR Assumptions, Estimation & Prediction
• 5.9- Further MLR Examples
• Lesson 6: MLR Assumptions, Estimation & Prediction
• Lesson 7: Transformations & Interactions
• Lesson 8: Categorical Predictors
• Lesson 9: Influential Points
• Lesson 10: Regression Pitfalls
• Lesson 11: Model Building
• Lesson 12: Logistic, Poisson & Nonlinear Regression
• Website for Applied Regression Modeling, 2nd edition
• Notation Used in this Course
• R Software Help
• Minitab Software Help

Copyright © 2018 The Pennsylvania State University Privacy and Legal Statements Contact the Department of Statistics Online Programs

Applied Data Science Meeting, July 4-6, 2023, Shanghai, China . Register for the workshops: (1) Deep Learning Using R, (2) Introduction to Social Network Analysis, (3) From Latent Class Model to Latent Transition Model Using Mplus, (4) Longitudinal Data Analysis, and (5) Practical Mediation Analysis. Click here for more information .

• Example Datasets
• Basics of R
• Graphs in R

Hypothesis testing

• Confidence interval
• Simple Regression
• Multiple Regression
• Logistic regression
• Moderation analysis
• Mediation analysis
• Path analysis
• Factor analysis
• Multilevel regression
• Longitudinal data analysis
• Power analysis

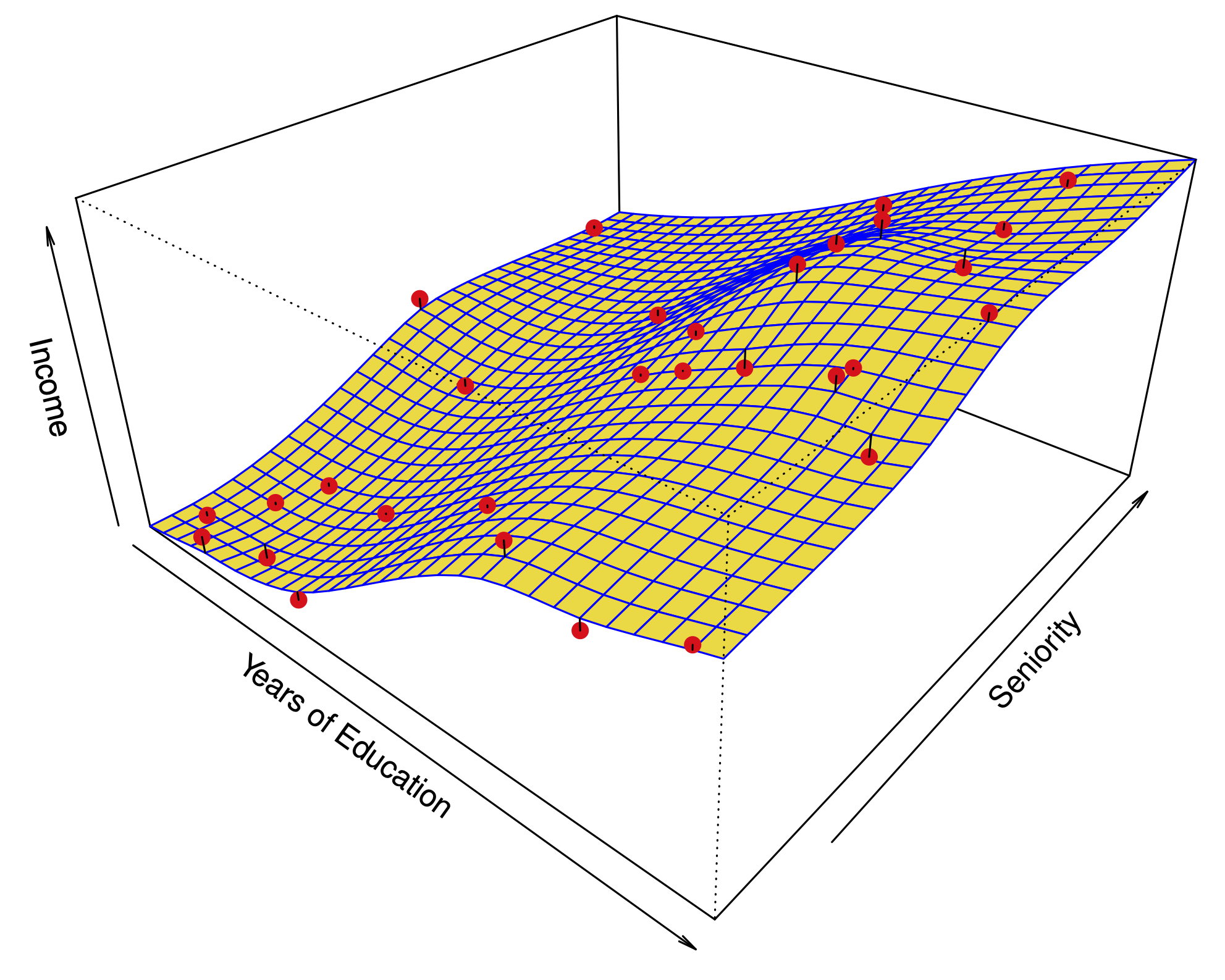
Multiple Linear Regression

The general purpose of multiple regression (the term was first used by Pearson, 1908), as a generalization of simple linear regression, is to learn about how several independent variables or predictors (IVs) together predict a dependent variable (DV). Multiple regression analysis often focuses on understanding (1) how much variance in a DV a set of IVs explain and (2) the relative predictive importance of IVs in predicting a DV.

In the social and natural sciences, multiple regression analysis is very widely used in research. Multiple regression allows a researcher to ask (and hopefully answer) the general question "what is the best predictor of ...". For example, educational researchers might want to learn what the best predictors of success in college are. Psychologists may want to determine which personality dimensions best predicts social adjustment.

Multiple regression model

A general multiple linear regression model at the population level can be written as

\[y_{i}=\beta_{0}+\beta_{1}x_{1i}+\beta_{2}x_{2i}+\ldots+\beta_{k}x_{ki}+\varepsilon_{i} \]

• $y_{i}$: the observed score of individual $i$ on the DV.
• $x_{1},x_{2},\ldots,x_{k}$ : a set of predictors.
• $x_{1i}$: the observed score of individual $i$ on IV 1; $x_{ki}$: observed score of individual $i$ on IV $k$.
• $\beta_{0}$: the intercept at the population level, representing the predicted $y$ score when all the independent variables have their values at 0.
• $\beta_{1},\ldots,\beta_{k}$: regression coefficients at the population level; $\beta_{1}$: representing the amount predicted $y$ changes when $x_{1}$ changes in 1 unit while holding the other IVs constant; $\beta_{k}$: representing the amount predicted $y$ changes when $x_{k}$ changes in 1 unit while holding the other IVs constant.
• $\varepsilon$: unobserved errors with mean 0 and variance $\sigma^{2}$.

Parameter estimation

The least squares method used for the simple linear regression analysis can also be used to estimate the parameters in a multiple regression model. The basic idea is to minimize the sum of squared residuals or errors. Let $b_{0},b_{1},\ldots,b_{k}$ represent the estimated regression coefficients.The individual $i$'s residual $e_{i}$ is the difference between the observed $y_{i}$ and the predicted $y_{i}$

\[ e_{i}=y_{i}-\hat{y}_{i}=y_{i}-b_{0}-b_{1}x_{1i}-\ldots-b_{k}x_{ki}.\]

The sum of squared residuals is

\[ SSE=\sum_{i=1}^{n}e_{i}^{2}=\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}. \]

By minimizing $SSE$, the regression coefficient estimates can be obtained as

\[ \boldsymbol{b}=(\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'\boldsymbol{y}=(\sum\boldsymbol{x}_{i}\boldsymbol{x}_{i}')^{-1}(\sum\boldsymbol{x}_{i}\boldsymbol{y}_{i}). \]

How well the multiple regression model fits the data can be assessed using the $R^{2}$. Its calculation is the same as for the simple regression

\[\begin{align*} R^{2} & = & 1-\frac{\sum e_{i}^{2}}{\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}\\& = & \frac{\text{Variation explained by IVs}}{\text{Total variation}} \end{align*}. \]

In multiple regression, $R^{2}$ is the total proportion of variation in $y$ explained by the multiple predictors.

The $R^{2}$ increases or at least is the same with the inclusion of more predictors. However, with more predators, the model becomes more complex and potentially more difficult to interpret. In order to take into consideration of the model complexity, the adjusted $R^{2}$ has been defined, which is calculated as

\[aR^{2}=1-(1-R^{2})\frac{n-1}{n-k-1}.\]

Hypothesis testing of regression coefficient(s)

With the estimates of regression coefficients and their standard errors estimates, we can conduct hypothesis testing for one, a subset, or all regression coefficients.

Testing a single regression coefficient

At first, we can test the significance of the coefficient for a single predictor. In this situation, the null and alternative hypotheses are

\[ H_{0}:\beta_{j}=0\text{ vs }H_{1}:\beta_{j}\neq0 \]

with $\beta_{j}$ denoting the regression coefficient of $x_{j}$ at the population level.

As in the simple regression, we use a test statistic

\[ t_{j}=\frac{b_{j} - \beta{j} }{s.e.(b_{j})}\]

where $b_{j}$ is the estimated regression coefficient of $x_{j}$ using data from a sample. If the null hypothesis is true and $\beta_j = 0$, the test statistic follows a t-distribution with degrees of freedom \(n-k-1\) where \(k\) is the number of predictors.

One can also test the significance of \(\beta_j\) by constructing a confidence interval for it. Based on a t distribution, the \(100(1-\alpha)%\) confidence interval is

\[ [b_{j}+t_{n-k-1}(\alpha/2)*s.e.(b_{j}),\;b_{j}+t_{n-k-1}(1-\alpha/2)*s.e.(b_{j})]\]

where $t_{n-k-1}(\alpha/2)$ is the $\alpha/2$ percentile of the t distribution. As previously discussed, if the confidence interval includes 0, the regression coefficient is not statistically significant at the significance level $\alpha$.

Testing all the regression coefficients together (overall model fit)

Given the multiple predictors, we can also test whether all of the regression coefficients are 0 at the same time. This is equivalent to test whether all predictors combined can explained a significant portion of the variance of the outcome variable. Since $R^2$ is a measure of the variance explained, this test is naturally related to it.

For this hypothesis testing, the null and alternative hypothesis are

\[H_{0}:\beta_{1}=\beta_{2}=\ldots=\beta_{k}=0\]

\[H_{1}:\text{ at least one of the regression coefficients is different from 0}.\]

In this kind of test, an F test is used. The F-statistic is defined as

\[F=\frac{n-k-1}{k}\frac{R^{2}}{1-R^{2}}.\]

It follows an F-distribution with degrees of freedom $k$ and $n-k-1$ when the null hypothesis is true. Given an F statistic, its corresponding p-value can be calculated from the F distribution as shown below. Note that we only look at one side of the distribution because the extreme values should be on the large value side.

Testing a subset of the regression coefficients

We can also test whether a subset of $p$ regression coefficients, e.g., $p$ from 1 to the total number coefficients $k$, are equal to zero. For convenience, we can rearrange all the $p$ regression coefficients to be the first $p$ coefficients. Therefore, the null hypothesis should be

\[H_{0}:\beta_{1}=\beta_{2}=\ldots=\beta_{p}=0\]

and the alternative hypothesis is that at least one of them is not equal to 0.

As for testing the overall model fit, an F test can be used here. In this situation, the F statistic can be calculated as

\[F=\frac{n-k-1}{p}\frac{R^{2}-R_{0}^{2}}{1-R^{2}},\]

which follows an F-distribution with degrees of freedom $p$ and $n-k-1$. $R^2$ is for the regression model with all the predictors and $R_0^2$ is from the regression model without the first $p$ predictors $x_{1},x_{2},\ldots,x_{p}$ but with the rest predictors $x_{p+1},x_{p+2},\ldots,x_{k}$.

Intuitively, this test determine whether the variance explained by the first \(p\) predictors above and beyond the $k-p$ predictors is significance or not. That is also the increase in R-squared.

As an example, suppose that we wanted to predict student success in college. Why might we want to do this? There's an ongoing debate in college and university admission offices (and in the courts) regarding what factors should be considered important in deciding which applicants to admit. Should admissions officers pay most attention to more easily quantifiable measures such as high school GPA and SAT scores? Or should they give more weight to more subjective measures such as the quality of letters of recommendation? What are the pros and cons of the approaches? Of course, how we define college success is also an open question. For the sake of this example, let's measure college success using college GPA.

In this example, we use a set of simulated data (generated by us). The data are saved in the file gpa.csv. As shown below, the sample size is 100 and there are 4 variables: college GPA (c.gpa), high school GPA (h.gpa), SAT, and quality of recommendation letters (recommd).

Graph the data

Before fitting a regression model, we should check the relationship between college GPA and each predictor through a scatterplot. A scatterplot can tell us the form of relationship, e.g., linear, nonlinear, or no relationship, the direction of relationship, e.g., positive or negative, and the strength of relationship, e.g., strong, moderate, or weak. It can also identify potential outliers.

The scatterplots between college GPA and the three potential predictors are given below. From the plots, we can roughly see all three predictors are positively related to the college GPA. The relationship is close to linear and the relationship seems to be stronger for high school GPA and SAT than for the quality of recommendation letters.

Descriptive statistics

Next, we can calculate some summary statistics to explore our data further. For each variable, we calculate 6 numbers: minimum, 1st quartile, median, mean, 3rd quartile, and maximum. Those numbers can be obtained using the summary() function. To look at the relationship among the variables, we can calculate the correlation matrix using the correlation function cor() .

Based on the correlation matrix, the correlation between college GPA and high school GPA is about 0.545, which is larger than that (0.523) between college GPA and SAT, in turn larger than that (0.35) between college GPA and quality of recommendation letters.

Fit a multiple regression model

As for the simple linear regression, The multiple regression analysis can be carried out using the lm() function in R. From the output, we can write out the regression model as

\[ c.gpa = -0.153+ 0.376 \times h.gpa + 0.00122 \times SAT + 0.023 \times recommd \]

Interpret the results / output

From the output, we see the intercept is -0.153. Its immediate meaning is that when all predictors' values are 0, the predicted college GPA is -0.15. This clearly does not make much sense because one would never get a negative GPA, which results from the unrealistic presumption that the predictors can take the value of 0.

The regression coefficient for the predictor high school GPA (h.gpa) is 0.376. This can be interpreted as keeping SAT and recommd scores constant , the predicted college GPA would increase 0.376 with a unit increase in high school GPA.This is again might be problematic because it might be impossible to increase high school GPA while keeping the other two predictors unchanged. The other two regression coefficients can be interpreted in the same way.

From the output, we can also see that the multiple R-squared ($R^2$) is 0.3997. Therefore, about 40% of the variation in college GPA can be explained by the multiple linear regression with h.GPA, SAT, and recommd as the predictors. The adjusted $R^2$ is slightly smaller because of the consideration of the number of predictors. In fact,

\[ \begin{eqnarray*} aR^{2} & = & 1-(1-R^{2})\frac{n-1}{n-k-1}\\& = & 1-(1-.3997)\frac{100-1}{100-3-1}\\& = & .3809 \end{eqnarray*} \]

Testing Individual Regression Coefficient

For any regression coefficients for the three predictors (also the intercept), a t test can be conducted. For example, for high school GPA, the estimated coefficient is 0.376 with the standard error 0.114. Therefore, the corresponding t statistic is \(t = 0.376/0.114 = 3.294\). Since the statistic follows a t distribution with the degrees of freedom \(df = n - k - 1 = 100 - 3 -1 =96\), we can obtain the p-value as \(p = 2*(1-pt(3.294, 96))= 0.0013\). Since the p-value is less than 0.05, we conclude the coefficient is statistically significant. Note the t value and p-value are directly provided in the output.

Overall model fit (testing all coefficients together)

To test all coefficients together or the overall model fit, we use the F test. Given the $R^2$, the F statistic is

\[ \begin{eqnarray*} F & = & \frac{n-k-1}{k}\frac{R^{2}}{1-R^{2}}\\ & = & \left(\frac{100-3-1}{3}\right)\times \left(\frac{0.3997}{1-.3997}\right )=21.307\end{eqnarray*} \]

which follows the F distribution with degrees of freedom $df1=k=3$ and $df2=n-k-1=96$. The corresponding p-value is 1.160e-10. Note that this information is directly shown in the output as " F-statistic: 21.31 on 3 and 96 DF, p-value: 1.160e-10 ".

Therefore, at least one of the regression coefficients is statistically significantly different from 0. Overall, the three predictors explained a significant portion of the variance in college GPA. The regression model with the 3 predictors is significantly better than the regression model with intercept only (i.e., predict c.gpa by the mean of c.gpa).

Testing a subset of regression coefficients

Suppose we are interested in testing whether the regression coefficients of high school GPA and SAT together are significant or not. Alternative, we want to see above and beyond the quality of recommendation letters, whether the two predictors can explain a significant portion of variance in college GPA. To conduct the test, we need to fit two models:

• A full model: which consists of all the predictors to predict c.gpa by intercept, h.gpa, SAT, and recommd.
• A reduced model: obtained by removing the predictors to be tested in the full model.

From the full model, we can get the $R^2 = 0.3997$ with all three predictors and from the reduced model, we can get the $R_0^2 = 0.1226$ with only quality of recommendation letters. Then the F statistic is constructed as

\[F=\frac{n-k-1}{p}\frac{R^{2}-R_{0}^{2}}{1-R^{2}}=\left(\frac{100-3-1}{2}\right )\times\frac{.3997-.1226}{1-.3997}=22.157.\]

Using the F distribution with the degrees of freedom $p=2$ (the number of coefficients to be tested) and $n-k-1 = 96$, we can get the p-value close to 0 ($p=1.22e-08$).

Note that the test conducted here is based on the comparison of two models. In R, if there are two models, they can be compared conveniently using the R function anova() . As shown below, we obtain the same F statistic and p-value.

To cite the book, use: Zhang, Z. & Wang, L. (2017-2022). Advanced statistics using R . Granger, IN: ISDSA Press. https://doi.org/10.35566/advstats. ISBN: 978-1-946728-01-2. To take the full advantage of the book such as running analysis within your web browser, please subscribe .

Multiple linear regression

Multiple linear regression #.

Fig. 11 Multiple linear regression #

Errors: \(\varepsilon_i \sim N(0,\sigma^2)\quad \text{i.i.d.}\)

Fit: the estimates \(\hat\beta_0\) and \(\hat\beta_1\) are chosen to minimize the residual sum of squares (RSS):

Matrix notation: with \(\beta=(\beta_0,\dots,\beta_p)\) and \({X}\) our usual data matrix with an extra column of ones on the left to account for the intercept, we can write

Multiple linear regression answers several questions #

Is at least one of the variables \(X_i\) useful for predicting the outcome \(Y\) ?

Which subset of the predictors is most important?

How good is a linear model for these data?

Given a set of predictor values, what is a likely value for \(Y\) , and how accurate is this prediction?

The estimates \(\hat\beta\) #

Our goal again is to minimize the RSS: $ \( \begin{aligned} \text{RSS}(\beta) &= \sum_{i=1}^n (y_i -\hat y_i(\beta))^2 \\ & = \sum_{i=1}^n (y_i - \beta_0- \beta_1 x_{i,1}-\dots-\beta_p x_{i,p})^2 \\ &= \|Y-X\beta\|^2_2 \end{aligned} \) $

One can show that this is minimized by the vector \(\hat\beta\) : $ \(\hat\beta = ({X}^T{X})^{-1}{X}^T{y}.\) $

We usually write \(RSS=RSS(\hat{\beta})\) for the minimized RSS.

Which variables are important? #

Consider the hypothesis: \(H_0:\) the last \(q\) predictors have no relation with \(Y\) .

Based on our model: \(H_0:\beta_{p-q+1}=\beta_{p-q+2}=\dots=\beta_p=0.\)

Let \(\text{RSS}_0\) be the minimized residual sum of squares for the model which excludes these variables.

The \(F\) -statistic is defined by: $ \(F = \frac{(\text{RSS}_0-\text{RSS})/q}{\text{RSS}/(n-p-1)}.\) $

Under the null hypothesis (of our model), this has an \(F\) -distribution.

Example: If \(q=p\) , we test whether any of the variables is important. $ \(\text{RSS}_0 = \sum_{i=1}^n(y_i-\overline y)^2 \) $

The \(t\) -statistic associated to the \(i\) th predictor is the square root of the \(F\) -statistic for the null hypothesis which sets only \(\beta_i=0\) .

A low \(p\) -value indicates that the predictor is important.

Warning: If there are many predictors, even under the null hypothesis, some of the \(t\) -tests will have low p-values even when the model has no explanatory power.

How many variables are important? #

When we select a subset of the predictors, we have \(2^p\) choices.

A way to simplify the choice is to define a range of models with an increasing number of variables, then select the best.

Forward selection: Starting from a null model, include variables one at a time, minimizing the RSS at each step.

Backward selection: Starting from the full model, eliminate variables one at a time, choosing the one with the largest p-value at each step.

Mixed selection: Starting from some model, include variables one at a time, minimizing the RSS at each step. If the p-value for some variable goes beyond a threshold, eliminate that variable.

Choosing one model in the range produced is a form of tuning . This tuning can invalidate some of our methods like hypothesis tests and confidence intervals…

How good are the predictions? #

The function predict in R outputs predictions and confidence intervals from a linear model:

Prediction intervals reflect uncertainty on \(\hat\beta\) and the irreducible error \(\varepsilon\) as well.

These functions rely on our linear regression model $ \( Y = X\beta + \epsilon. \) $

Dealing with categorical or qualitative predictors #

For each qualitative predictor, e.g. Region :

Choose a baseline category, e.g. East

For every other category, define a new predictor:

\(X_\text{South}\) is 1 if the person is from the South region and 0 otherwise

\(X_\text{West}\) is 1 if the person is from the West region and 0 otherwise.

The model will be: $ \(Y = \beta_0 + \beta_1 X_1 +\dots +\beta_7 X_7 + \color{Red}{\beta_\text{South}} X_\text{South} + \beta_\text{West} X_\text{West} +\varepsilon.\) $

The parameter \(\color{Red}{\beta_\text{South}}\) is the relative effect on Balance (our \(Y\) ) for being from the South compared to the baseline category (East).

The model fit and predictions are independent of the choice of the baseline category.

However, hypothesis tests derived from these variables are affected by the choice.

Solution: To check whether region is important, use an \(F\) -test for the hypothesis \(\beta_\text{South}=\beta_\text{West}=0\) by dropping Region from the model. This does not depend on the coding.

Note that there are other ways to encode qualitative predictors produce the same fit \(\hat f\) , but the coefficients have different interpretations.

So far, we have:

Defined Multiple Linear Regression

Discussed how to test the importance of variables.

Described one approach to choose a subset of variables.

Explained how to code qualitative variables.

Now, how do we evaluate model fit? Is the linear model any good? What can go wrong?

How good is the fit? #

To assess the fit, we focus on the residuals $ \( e = Y - \hat{Y} \) $

The RSS always decreases as we add more variables.

The residual standard error (RSE) corrects this: $ \(\text{RSE} = \sqrt{\frac{1}{n-p-1}\text{RSS}}.\) $

Fig. 12 Residuals #

Visualizing the residuals can reveal phenomena that are not accounted for by the model; eg. synergies or interactions:

Potential issues in linear regression #

Interactions between predictors

Non-linear relationships

Correlation of error terms

Non-constant variance of error (heteroskedasticity)

High leverage points

Collinearity

Interactions between predictors #

Linear regression has an additive assumption: $ \(\mathtt{sales} = \beta_0 + \beta_1\times\mathtt{tv}+ \beta_2\times\mathtt{radio}+\varepsilon\) $

i.e. An increase of 100 USD dollars in TV ads causes a fixed increase of \(100 \beta_2\) USD in sales on average, regardless of how much you spend on radio ads.

We saw that in Fig 3.5 above. If we visualize the fit and the observed points, we see they are not evenly scattered around the plane. This could be caused by an interaction.

One way to deal with this is to include multiplicative variables in the model:

The interaction variable tv \(\cdot\) radio is high when both tv and radio are high.

R makes it easy to include interaction variables in the model:

Non-linearities #

Fig. 13 A nonlinear fit might be better here. #

Example: Auto dataset.

A scatterplot between a predictor and the response may reveal a non-linear relationship.

Solution: include polynomial terms in the model.

Could use other functions besides polynomials…

Fig. 14 Residuals for Auto data #

In 2 or 3 dimensions, this is easy to visualize. What do we do when we have too many predictors?

Correlation of error terms #

We assumed that the errors for each sample are independent:

What if this breaks down?

The main effect is that this invalidates any assertions about Standard Errors, confidence intervals, and hypothesis tests…

Example : Suppose that by accident, we duplicate the data (we use each sample twice). Then, the standard errors would be artificially smaller by a factor of \(\sqrt{2}\) .

When could this happen in real life:

Time series: Each sample corresponds to a different point in time. The errors for samples that are close in time are correlated.

Spatial data: Each sample corresponds to a different location in space.

Grouped data: Imagine a study on predicting height from weight at birth. If some of the subjects in the study are in the same family, their shared environment could make them deviate from \(f(x)\) in similar ways.

Correlated errors #

Simulations of time series with increasing correlations between \(\varepsilon_i\)

Non-constant variance of error (heteroskedasticity) #

The variance of the error depends on some characteristics of the input features.

To diagnose this, we can plot residuals vs. fitted values:

If the trend in variance is relatively simple, we can transform the response using a logarithm, for example.

Outliers from a model are points with very high errors.

While they may not affect the fit, they might affect our assessment of model quality.

Possible solutions: #

If we believe an outlier is due to an error in data collection, we can remove it.

An outlier might be evidence of a missing predictor, or the need to specify a more complex model.

High leverage points #

Some samples with extreme inputs have an outsized effect on \(\hat \beta\) .

This can be measured with the leverage statistic or self influence :

Studentized residuals #

The residual \(e_i = y_i - \hat y_i\) is an estimate for the noise \(\epsilon_i\) .

The standard error of \(\hat \epsilon_i\) is \(\sigma \sqrt{1-h_{ii}}\) .

A studentized residual is \(\hat \epsilon_i\) divided by its standard error (with appropriate estimate of \(\sigma\) )

When model is correct, it follows a Student-t distribution with \(n-p-2\) degrees of freedom.

Collinearity #

Two predictors are collinear if one explains the other well:

Problem: The coefficients become unidentifiable .

Consider the extreme case of using two identical predictors limit : $ \( \begin{aligned} \mathtt{balance} &= \beta_0 + \beta_1\times\mathtt{limit} + \beta_2\times\mathtt{limit} + \epsilon \\ & = \beta_0 + (\beta_1+100)\times\mathtt{limit} + (\beta_2-100)\times\mathtt{limit} + \epsilon \end{aligned} \) $

For every \((\beta_0,\beta_1,\beta_2)\) the fit at \((\beta_0,\beta_1,\beta_2)\) is just as good as at \((\beta_0,\beta_1+100,\beta_2-100)\) .

If 2 variables are collinear, we can easily diagnose this using their correlation.

A group of \(q\) variables is multilinear if these variables “contain less information” than \(q\) independent variables.

Pairwise correlations may not reveal multilinear variables.

The Variance Inflation Factor (VIF) measures how predictable it is given the other variables, a proxy for how necessary a variable is:

Above, \(R^2_{X_j|X_{-j}}\) is the \(R^2\) statistic for Multiple Linear regression of the predictor \(X_j\) onto the remaining predictors.