High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:

Surface area
Lucy Inskip
Here you will learn about surface area, including what it is and how to calculate it for prisms and pyramids.
Students will first learn about surface area as part of geometry in 6 th grade.
What is surface area?
The surface area is the total area of all of the faces of a three-dimensional shape. This includes prisms and pyramids. The surface area is always recorded in square units.
Prisms are 3D shapes that have a polygonal base and rectangular faces. A rectangular prism has 6 rectangular faces, including 4 rectangular lateral faces and 2 rectangular bases.
For example,
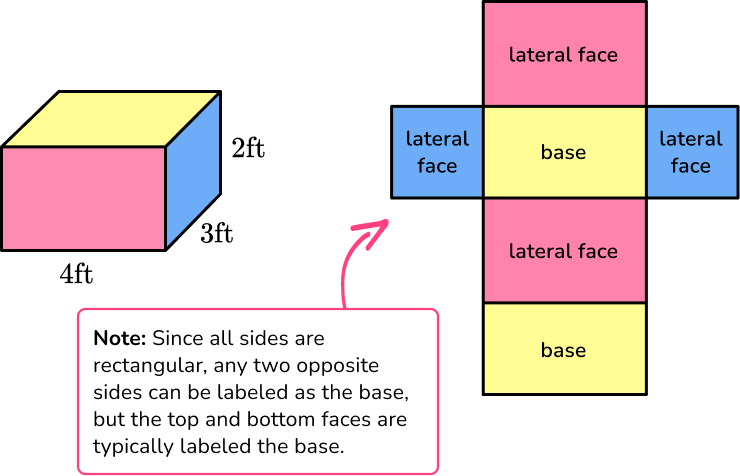
Calculate the area of each face and then add them together for the surface area of the rectangular prism.
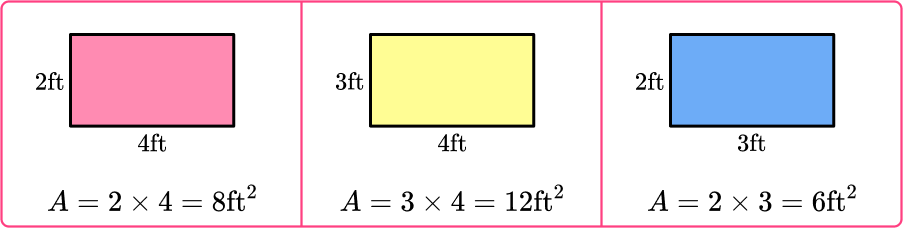
The surface area of the prism is the sum of the areas. Add each area twice, since each rectangle appears twice in the prism:
8+8+12+12+6+6=52 \, f t^2
You can also find the surface area by multiplying each area by 2 and then adding.
(2 \times 8)+(2 \times 12)+(2 \times 6)=52 \, f t^2
Step-by-step guide: Surface area of rectangular prism
![problem solving in surface area [FREE] Surface Area Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/04/Surface-Area-Worksheet-listing-image.png)
[FREE] Surface Area Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of surface area. 15 questions with answers to identify areas of strength and support!
Another type of prism is a triangular prism.
A triangular prism is made up of 5 faces, including 2 triangular bases and 3 rectangular lateral faces.
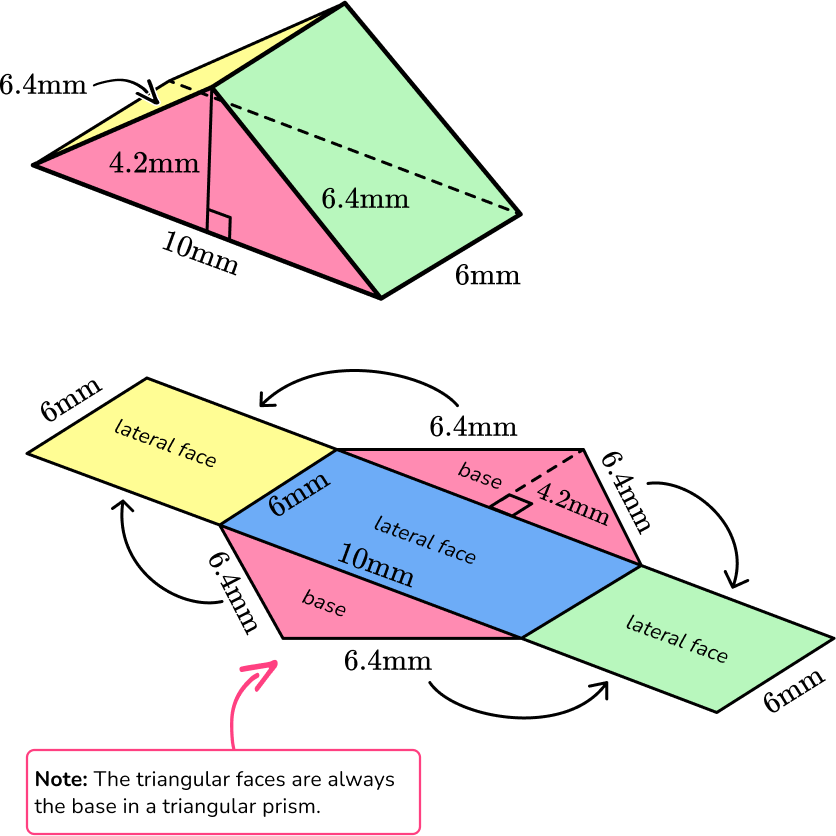
Calculate the area of each face and then add them together for the surface area of the triangular prism.
\begin{aligned} A&=6 \times 6.4 \\ &=38.4 \mathrm{~mm}^2 \end{aligned} | \begin{aligned} A&=6 \times 10 \\ &=60 \mathrm{~mm}^2 \end{aligned} | \begin{aligned} A&=6 \times 6.4 \\ &=38.4 \mathrm{~mm}^2 \end{aligned} | \begin{aligned} A&=\frac{1}{2} \times 10 \times 4.2 \\ &=21 \mathrm{~mm}^2 \end{aligned} |
The surface area of the prism is the sum of the areas. Add the area of the triangular base twice (or you can multiply it by 2 ), since it appears twice in the prism:
37.2+60+38.4+21+21=177.6 \mathrm{~mm}^2
Step-by-step guide: Surface area of triangular prism
Step-by-step guide: Surface area of a prism
Pyramids are another type of 3D shape. A pyramid is made up of a polygonal base and triangular lateral sides.
All lateral faces (sides) of this square pyramid are congruent.
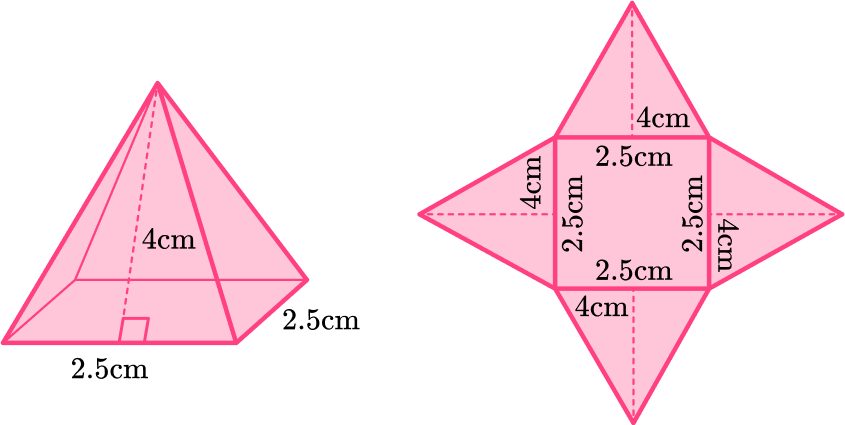
To calculate the surface area of a pyramid , calculate the area of each face of the pyramid and then add the areas together.
\text {Area of the base }=2.5 \times 2.5=6.25 \mathrm{~cm}^2
\text {Area of a triangular face }=\cfrac{1}{2} \times 2.5 \times 4=5 \mathrm{~cm}^2
Add the area of the base and the 4 congruent triangular faces:
\text {Surface area }=6.25+5+5+5+5=6.25+(4 \times 5)=26.25 \mathrm{~cm}^2
The total surface area can also be written in one equation:
\begin{aligned} \text {Surface area of pyramid } & =\text {Area of base }+ \text {Areas of triangular faces } \\\\ & =2.5^2+4 \times\left(\cfrac{1}{2} \, \times 2.5 \times 4\right) \\\\ & =6.25+20 \\\\ & =26.25 \mathrm{~cm}^2 \end{aligned}
Step-by-step guide: Surface area of a pyramid
Common Core State Standards
How does this relate to 6 th grade math?
- Grade 6 – Geometry (6.G.A.4) Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures. Apply these techniques in the context of solving real-world and mathematical problems.
How to calculate the surface area of a prism
In order to calculate the surface area:
Calculate the area of each face.
Add the area of each face together.
Include the units.
Surface area examples
Example 1: surface area of a rectangular prism.
Calculate the surface area of the rectangular prism.

A rectangular prism has 6 faces, with 3 pairs of identical faces.
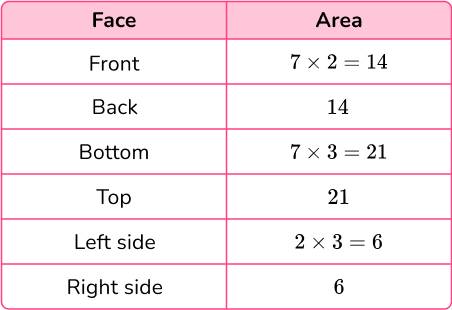
2 Add the area of each face together.
Total surface area: 14+14+21+21+6+6=82
Since opposite rectangles are always congruent, you can also use multiplication to solve:
Total surface area: 14 \times 2+21 \times 2+6 \times 2=82
3 Include the units.
The measurements on this prism are in m , so the total surface area of the prism is 82 \mathrm{~m}^2.
Example 2: surface area of a triangular prism with an equilateral triangle – using a net
Calculate the surface area of the triangular prism. The base of the prism is an equilateral triangle with a perimeter of 16.5 \, ft.

First, use the perimeter of the base to find the length of each side. Since an equilateral triangle has all equal sides, s , the perimeter is s+s+s=16.5.
s=5.5 \, ft
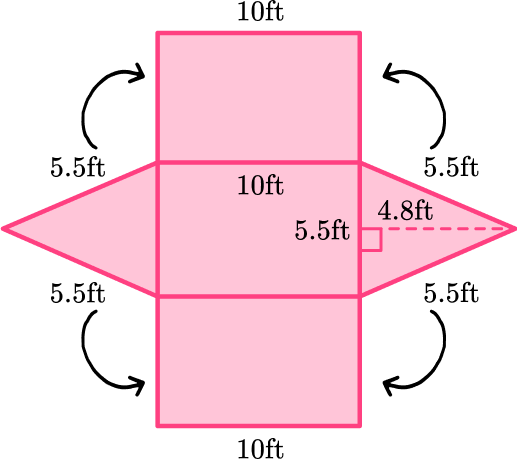
You can unfold the triangular prism, and use the net to find the area of each face:
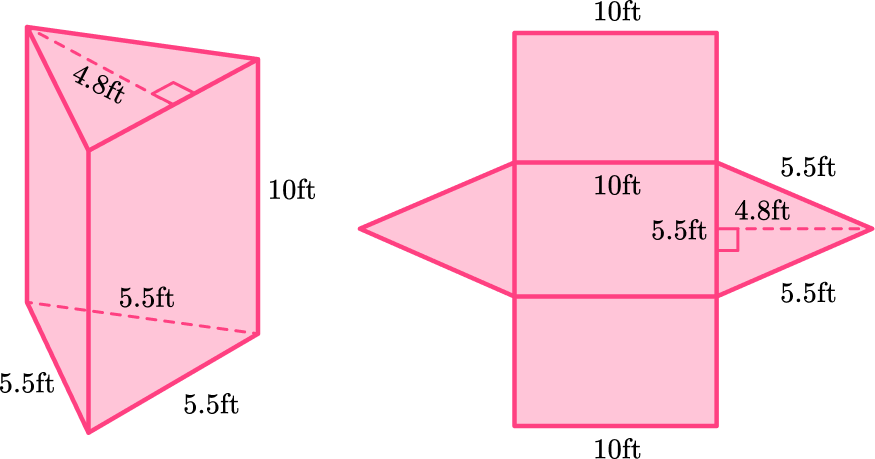
Remember that the edges in a prism are always equal, so if you were to fold up the net, the 5.5 \, ft side of the triangle would combine to form an edge with each corresponding rectangle – making their lengths equal.
The area of each triangular base:
\cfrac{1}{2} \times 4.8 \times 5.5=13.2
The area of each rectangular lateral face:
10 \times 5.5=55
If you have trouble keeping track of all the calculations, use a net:
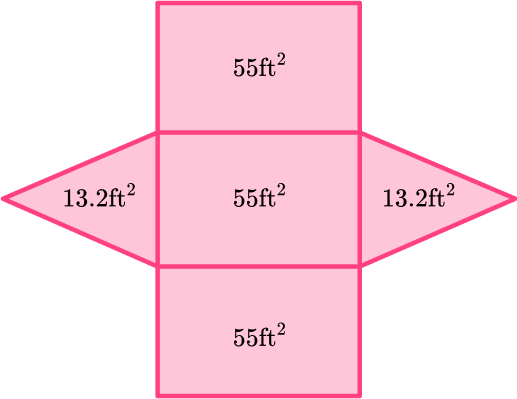
The area of the base is always equal to the area of the opposite base, in this case the triangles.
Notice, since the triangle is equilateral, all the rectangular faces are equal as well.
Total surface area: 13.2+13.2+55+55+55=191.4
The measurements on this prism are in ft , so the total surface area of the prism is 191.4 \mathrm{~ft}^2.
Example 3: surface area of a square-based pyramid in cm
All the lateral faces of the pyramid are congruent. Calculate the surface area.
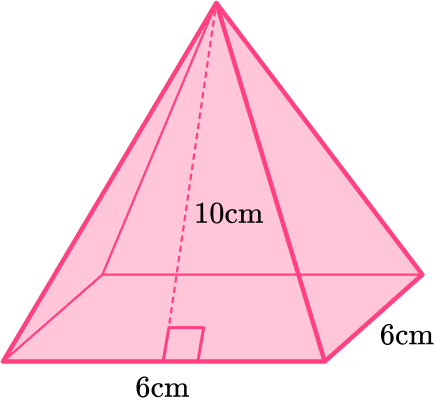
The base is a square with the area 6\times{6}=36\text{~cm}^2.
All four triangular faces are identical, so calculate the area of one triangle, and then multiply the area by 4 .
\begin{aligned} A&= \cfrac{1}{2} \, \times{b}\times{h}\\\\ &=\cfrac{1}{2} \, \times{10}\times{6}\\\\ &=30 \end{aligned}
30\times{4}=120
Add the area of the base and the area of the four triangles:
SA=36+120=156
The side lengths are measured in centimeters, so the area is measured in square centimeters.
SA=156\text{~cm}^{2}
Example 4: surface area of a rectangular prism – using a net
Calculate the lateral surface area of the rectangular prism. The base of the prism is a square and one side of the base measures 3 \, \cfrac{2}{3} inches.
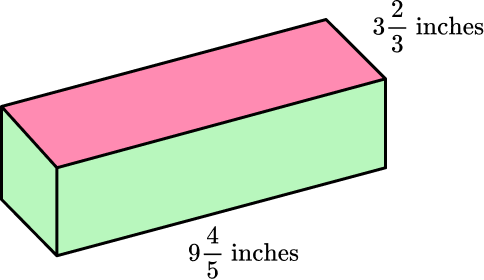
You can unfold the rectangular prism, and use the net to find the area of each face:
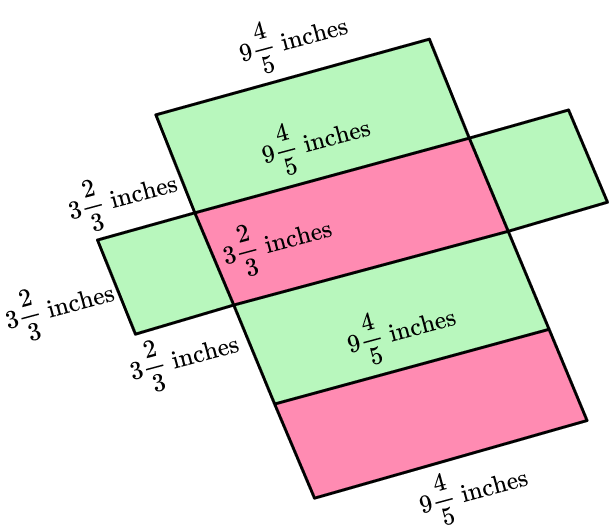
Remember that the edges in a prism are always equal, so if you were to fold up the net, the 3 \cfrac{2}{3} \mathrm{~ft} side of the square would combine to form an edge with each corresponding rectangle – making their lengths equal.
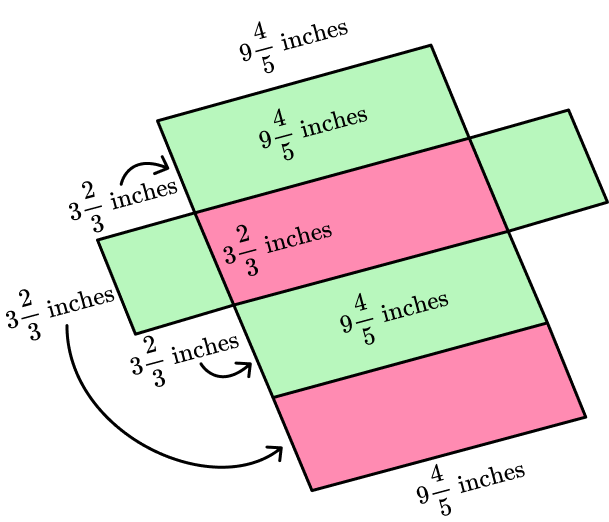
\begin{aligned} & 9 \cfrac{4}{5} \, \times 3 \, \cfrac{2}{3} \\\\ &= \cfrac{49}{5} \, \times \cfrac{11}{3} \\\\ &= \cfrac{539}{15} \\\\ &= 35 \, \cfrac{14}{15} \end{aligned}
Remember, you are only finding the area of the lateral faces, so you do not need to calculate the area of the bases.
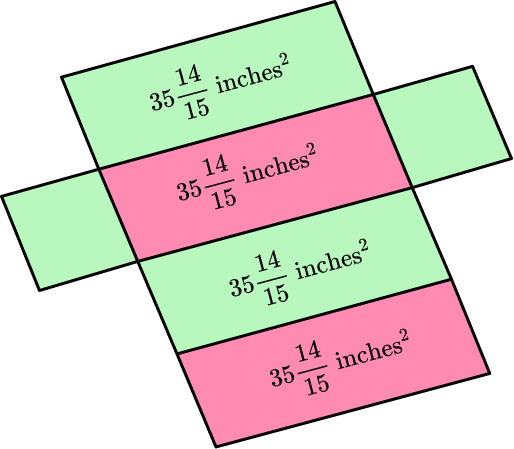
Notice, since the square has all equal sides, all the rectangular faces are equal as well.
Total lateral surface area:
\begin{aligned} & 35 \, \cfrac{14}{15}+35 \, \cfrac{14}{15}+35 \, \cfrac{14}{15}+35 \, \cfrac{14}{15} \\\\ & =140 \, \cfrac{56}{15} \\\\ & =143 \, \cfrac{11}{15} \end{aligned}
Since all the lateral faces are congruent, you can also use multiplication to solve:
\begin{aligned} & 4 \times 35 \, \cfrac{14}{15} \\\\ & =\cfrac{4}{1} \, \times \, \cfrac{539}{15} \\\\ & =\cfrac{2,156}{15} \\\\ & =143 \, \cfrac{11}{15} \end{aligned}
The measurements on this prism are in inches, so the total lateral surface area of the prism is 143 \, \cfrac{11}{15} \text {~inches }^2.
Example 5: surface area of a parallelogram prism with different units
Calculate the surface area of the parallelogram prism.
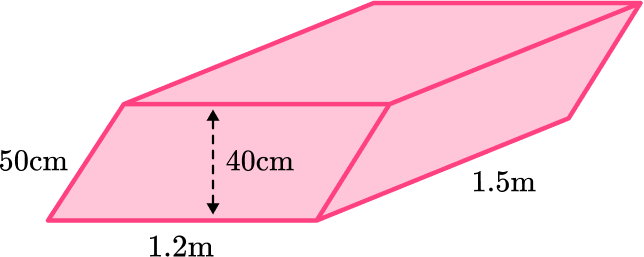
A parallelogram prism has 6 faces and, like a rectangular prism, it has 3 pairs of identical faces. The base is a parallelogram and all of the lateral faces are rectangular.
In this example, some of the measurements are in cm and some are in m . You must convert the units so that they are the same. Convert all the units to meters (m)\text{: } 40 {~cm}=0.4 {~m} and 50 {~cm}=0.5 {~m}.
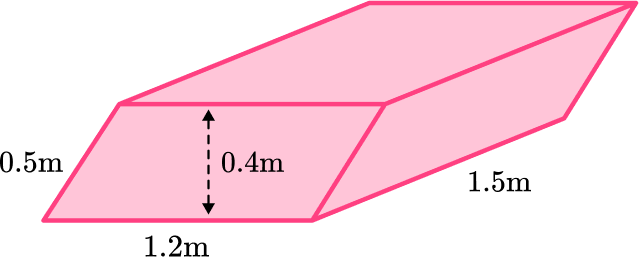
Total surface area: 0.48+0.48+1.8+1.8+0.75+0.75=6.06
The measurements that we have used are in m so the surface area of the prism is 6.06 \mathrm{~m}^2.
Example 6: surface area of a square pyramid – word problem
Mara is making a square pyramid out of cardboard. She cut out 4 acute triangles that have a base of 5 inches and a height of 7.4 inches. How much cardboard will she need to complete the entire square pyramid?
The lateral faces are all congruent, acute triangles.
\begin{aligned} \text {Area of triangle } & =\cfrac{1}{2} \, \times 5 \times 7.4 \\\\ & =18.5 \end{aligned}
Since it is a square pyramid, the base is a square. Each side of the square shares an edge with the base of the triangle, so each side of the square is 5 .
\begin{aligned} \text { Area of square } & =5 \times 5 \\\\ & =25 \end{aligned}
There is one square base and 4 congruent lateral triangular faces.
Total surface area: 25+18.5 \times 4=25+74=99
The measurements on this prism are in inches, so the total surface area of the prism is 99 \text {~inches}^2.
Teaching tips for the surface area of a prism
- Make sure that students have had time to work with physical 3D models and nets before doing activities that involve finding the surface area of pyramids and prisms.
- Choose worksheets that offer a variety of question types – a mixture of showing the full pyramid or prism versus showing the net, a mixture of solving for the missing surface area versus a missing dimension, and one that includes some word problems.
Easy mistakes to make

- Confusing lateral area with total surface area Lateral area is the area of each of the sides, and total surface area is the area of the bases plus the area of the sides. When asked to find the lateral area, be sure to only add up the area of the sides – which are always rectangles in right prisms (the types of prisms shown on this page). Note: In oblique prisms the lateral faces are parallelograms.
Practice surface area of a prism questions
1) The pyramid is composed of four congruent equilateral triangles. Find the surface area of the pyramid.
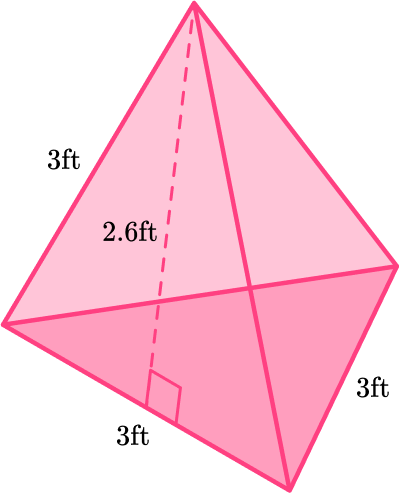
\begin{aligned} \text {Surface area of pyramid }&= \text { Area of base and faces} \\ & \quad \text{ (4 congruent triangles) } \\\\ & =4 \times\left(\cfrac{1}{2} \, \times 3 \times 2.6\right) \\\\ & =4 \times 3.9 \\\\ & =15.6 \mathrm{~ft}^2 \end{aligned}
2) Calculate the surface area of the triangular prism:
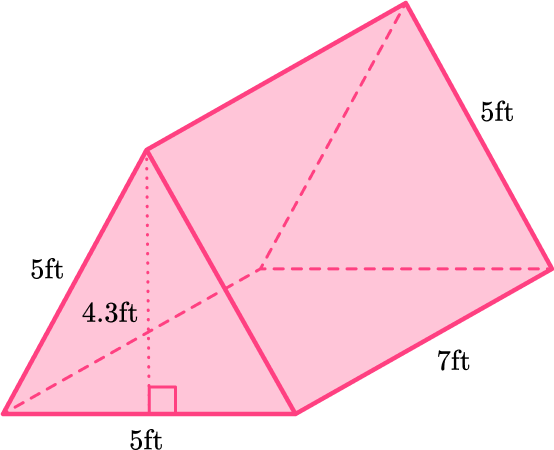
You can unfold the triangular prism, and use the net to find the area of each face.
Remember that the edges in a prism always fold up together to form the prism – making their lengths equal.
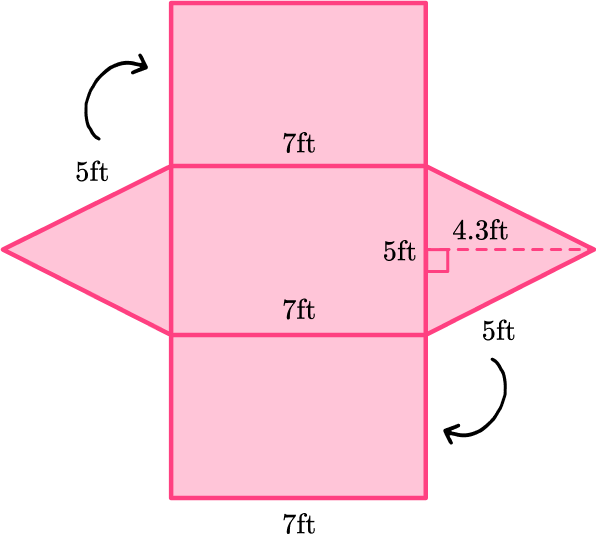
\cfrac{1}{2} \times 5 \times 4.3=10.75
7 \times 5=35

Total surface area: 10.75+10.75+35+35+35=126.5 \mathrm{~ft}^2
3) Calculate the surface area of the rectangular prism:
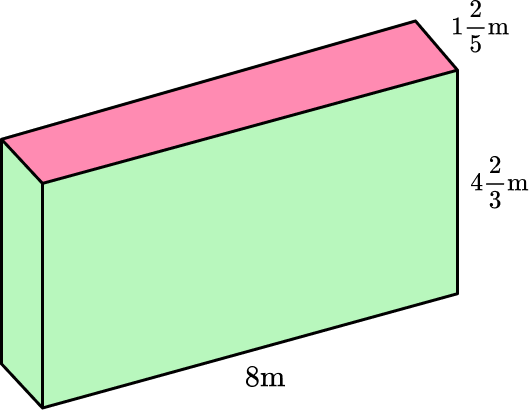
You can unfold the rectangular prism, and use the net to find the area of each face.
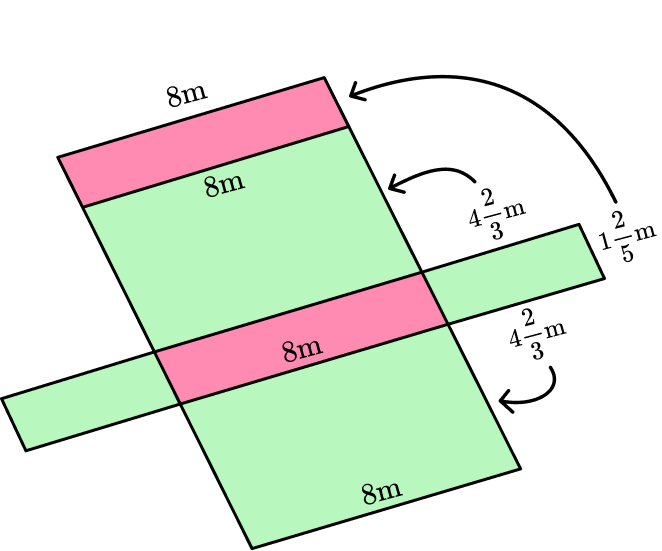
The area of each rectangular base:
\begin{aligned} & 1 \cfrac{2}{5} \, \times 8 \\\\ &= \cfrac{7}{5} \, \times \cfrac{8}{1} \\\\ &= \cfrac{56}{5} \\\\ &= 11 \, \cfrac{1}{5} \end{aligned}
\begin{aligned} & 4 \, \cfrac{2}{3} \, \times 8 \\\\ &= \cfrac{14}{3} \, \times \cfrac{8}{1} \\\\ &= \cfrac{112}{3} \\\\ &= 37 \, \cfrac{1}{3} \end{aligned}
\begin{aligned} & 4 \, \cfrac{2}{3} \, \times 1 \cfrac{2}{5} \\\\ &= \cfrac{14}{3} \, \times \cfrac{7}{5} \\\\ &= \cfrac{98}{15} \\\\ &= 6 \cfrac{8}{15} \end{aligned}
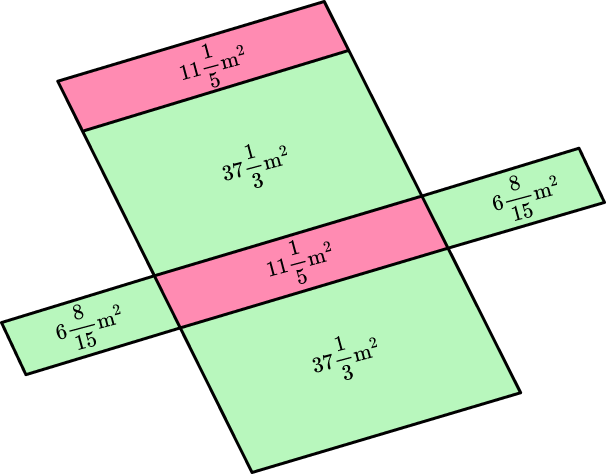
Total surface area:
\begin{aligned} & 6 \, \cfrac{8}{15} \, +6 \, \cfrac{8}{15} \, +11 \, \cfrac{1}{5} \, +11 \, \cfrac{1}{5} \, +37 \, \cfrac{1}{3} \, +37 \, \cfrac{1}{3} \\\\ & =6 \, \cfrac{8}{15} \, +6 \, \cfrac{8}{15} \, +11 \, \cfrac{5}{15} , +11 \, \cfrac{5}{15} \, +37 \, \cfrac{3}{15} \, +37 \, \cfrac{3}{15} \\\\ & =108 \, \cfrac{32}{15} \\\\ & =110 \, \cfrac{2}{15} \mathrm{~m}^2 \end{aligned}
4) Here is a net of a square pyramid. Calculate the surface area.

\begin{aligned} \text {Area of triangle } & =\cfrac{1}{2} \, \times 6.5 \times 3.8 \\\\ & =12.35 \end{aligned}
Since it is a square pyramid, the base is a square.
\begin{aligned} \text {Area of square } & =6.5 \times 6.5 \\\\ & =42.25 \end{aligned}
Total surface area = 12.35+12.35+12.35+12.35+42.25=91.65 \mathrm{~m}^2
5) Calculate the surface area of the prism.
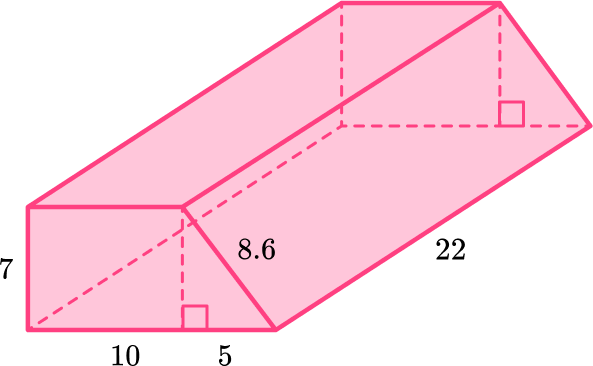
The congruent bases (front and back faces) are composed of a rectangle and a right triangle.
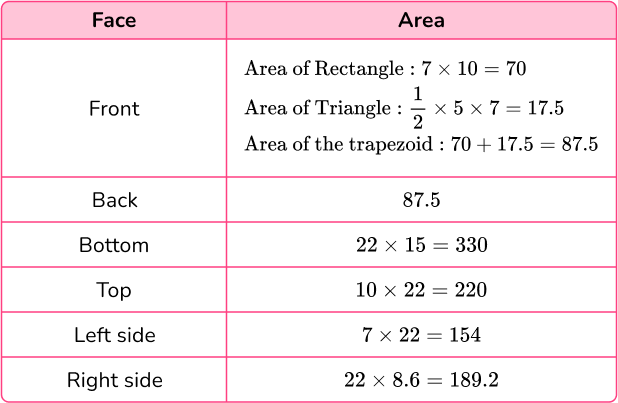
Total surface area = 87.5+87.5+330+220+154+189.2=1,068 .2 \text { units}^2
6) Malika was painting the hexagonal prism below. It took 140.8 \text { inches}^2 to cover the entire shape. If the area of the base is \text {10.4 inches}^2 and each side of the hexagon is 2 \text { inches} , what is the height of the prism?

You can unfold the hexagonal prism, and use the net to find the area of each face:
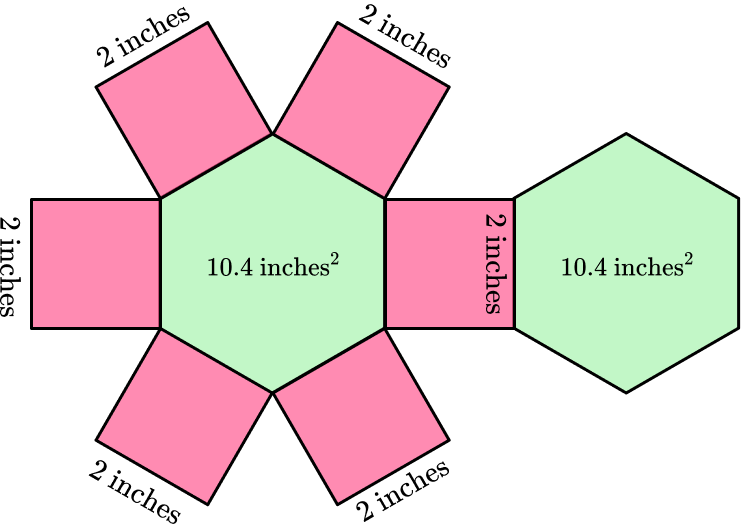
Total area of the bases: 10.4+10.4=20.8
Subtract the area of the bases from the total amount of paint Malika used, to see how much was used on the lateral faces:
140.8-20.8=120
The total area of the faces left is 120 \text { inches}^2.
Since the 6 faces are congruent, the total for each face can be found by dividing by 6\text{:}
120 \div 6=20
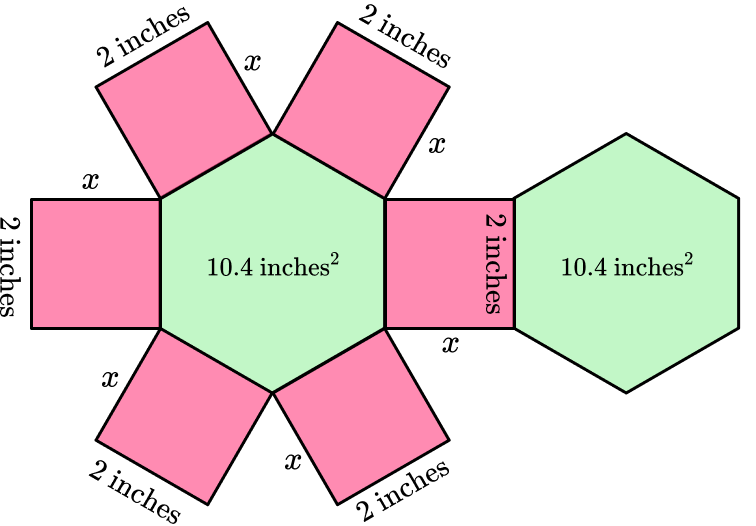
Labeling the missing length as x , means the area of each face can be written as 2 \times x or 2 x .
Since each face has an area of 20 \text{ inches}^2 , the missing height can be found with the equation: 2 x=20.
Since 2 \times 10=20 , the missing height is 10 inches.
Surface area FAQs
A cuboid is a prism with a rectangular base and rectangular lateral sides. It is also known as a rectangular prism.
Some shapes do have a general formula that you can use. For example, the surface area of a rectangular prism uses the formula 2 \: (l b+b h+l h) . There are other formulas, but for all prisms, the general formula is \text {area of } 2 \text { bases }+ \text {area of all lateral faces} .
Since all the faces have the same area, find the area of the square base and multiply it by 6 . Step-by-step guide : Surface area of a cube
The surface area of a cylinder is the area of a circle (the two congruent bases) plus the the curved surface area (2 \pi r h). . This will give you the surface area of the cylinder. Step-by-step guide: Surface area of a cylinder
To find the curved surface area, square the radius of the sphere and multiply it by 4 \pi . This will give you the surface area of the sphere. Step-by-step guide : Surface area of a sphere
The next lessons are
- Pythagorean theorem
- Trigonometry
- Circle math
- Surface area of a cone
- Surface area of a hemisphere
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!
Privacy Overview

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Geometry >
Surface Area Worksheets
Surface area worksheets comprise an enormous collection of exercises on different solid figures. The large chunk of exercises is categorized based on a step-by-step approach involving counting unit squares to determine the SA, finding the surface area of nets, and then computing the surface area of geometrical shapes like cubes, cones, cylinders, rectangular prisms, L-shaped prisms, spheres, hemispheres, pyramids, and composite figures, catering to the needs of students in 5th grade through high school. Revisiting surface area is easy with our mixed 3D shapes revision pdfs. Count on our free printable SA worksheets for a great start!
List of Surface Area Worksheets
- Surface Area of 3D Figures Using Nets
- Surface Area by Counting Squares
- Surface Area of Cubes
- Surface Area of Rectangular Prisms
- Surface Area of L-Shaped Prisms
- Surface Area of Triangular Prisms
- Surface Area of Cylinders
- Surface Area of Prisms and Cylinders
- Surface Area of Cones
- Surface Area of Spheres and Hemispheres
- Surface Area of Pyramids
- Surface Area of Mixed Solid Shapes
- Surface Area of Composite Figures
Explore the Surface Area Worksheets in Detail
Surface Area of 3D Figures Using Nets Worksheets
Finding the surface area of 3D figures using nets worksheets assist students in visualizing the surface of solid shapes whose nets are sketched on grids. Add on to their practice in determining the SA of the nets of 3D shapes like cylinders, cones, and pyramids, and in drawing the nets of solid figures too.
Surface Area by Counting Squares Worksheets
Start off with counting unit squares on an isometric paper, follow up by drawing the correct number of squares, and then find the SA of rectangular prisms by counting the squares scaled to varied units. These interesting exercises make the surface area by counting squares pdfs a compulsive print for your grade 5 and grade 6 students.
Surface Area of Cubes Worksheets
Page through these surface area of a cube exercises to practice computing the total area occupied by the cubes with edge length offered as integers, decimals and fractions. Included here are pdfs to find the missing edge length using the SA and more.
Surface Area of Rectangular Prisms Worksheets
Surface area of rectangular prisms handouts are a sure-fire hit in every grade 6, grade 7, and grade 8 geometry curriculum. Find the SA using the height, width, and length, and extend your practice to finding the missing dimensions as well.
Surface Area of L-Shaped Prisms Worksheets
Lay a strong foundation in decomposing shapes with these printable surface area of L-shaped rectangular prism worksheets. Solve for surface area of independent 3D shapes, add them, and subtract the area of the face that connects the rectangular blocks.
Surface Area of Triangular Prisms Worksheets
Expedite practice calculating the surface area of triangular prisms with these worksheet pdfs, rendering the attributes of the triangular bases and rectangular side faces of the figure, in integers and decimals.
Surface Area of Cylinders Worksheets
The surface area of a cylinder pdfs feature solid shapes, each made up of a curved surface with two circular bases. Recall the formula for SA of a cylinder, plug in the integer, decimal, or fractional radius measures in the formula 2πrh + 2πr 2 and compute.
Surface Area of Prisms and Cylinders Worksheets
A mix of rectangular prisms, triangular prisms, and cylinders is what these printable worksheets have in store for your middle and high school learners. Consider memorizing the SA formulas, apply the one relevant to the solid shape, substitute the dimensions and solve.
Surface Area of Cones Worksheets
Give your 6th grade, 7th grade, and 8th grade students an edge over their peers with these surface area of cones exercises. Supplying the values of the dimensions in the formula and calculating the surface area of cones is all that is expected of learners.
Surface Area of Spheres and Hemispheres Worksheets
Build fluency and competence with this collection of surface area of spheres and hemispheres worksheets. Get students to find the TSA of the hemispheres and CSA of the spheres by substituting the dimensions in relevant formulas.
Surface Area of Pyramids Worksheets
Handle these printable surface area of pyramid practice sheets with great dexterity. Learn the know-how of finding the surface area of pyramids applying relevant formulas and substituting the dimensions accordingly.
Surface Area of Mixed Solid Shapes Worksheets
How well do your 8th grade and high school students remember the SA formulas of solid shapes like cubes, cones, cylinders, spheres, hemispheres, prisms and pyramids? Check for yourself with these surface area of solid shapes revision pdfs.
Surface Area of Composite Figures Worksheets
Tee up to decompose each combined shape, find the sum of the SA of individual 3D shapes, subtract the area of the common parts, and determine the SA like a pro with this set of printable surface area of composite shapes worksheets.
Sample Worksheets
Become a Member
Membership Information
Printing Help
How to Use Online Worksheets
How to Use Printable Worksheets
Privacy Policy
Terms of Use
Copyright © 2024 - Math Worksheets 4 Kids
Surface Area
Types of surface area, how do you find surface area, surface area of some common shapes.
- Real-Life Applications of Surface Area Calculation
Solved Examples
Practice problems, frequently asked questions.
The sum of the area of all the surfaces of a three-dimensional object is measured as its surface area. It depends on the total number of faces, edges, and vertices that make up an object's external surface. Surface area is a crucial geometric feature in numerous fields, including mathematics, engineering, physics, and architecture.
It can be understood simply by imagining wrapping an object using paper. The surface area of the object would be represented by the total area of the paper utilized to cover its complete surface.
For example, the surface area of a rectangular box would include the area of each of the six faces of the box. Whether a face is curved (like the objects with circular top and bottom) or flat (like the box's sides), each adds to the overall surface area. In the same way, the surface area of a sphere includes the area of its curved surface. In short, the surface area is the entire area that covers all exterior surfaces of a three-dimensional object.
Surface area refers to the total area of the external surface of a three-dimensional object. Here are some common types of surface area:
`1`. Base Area
Base area refers to the area of the bottom or top surface of a three-dimensional object. For objects with a well-defined base, such as a cylinder or pyramid, the base area is the area of the circle, triangle, or any polygon that acts as the base of the object.
`2`. Lateral Surface Area
The lateral surface area is the total surface area of a three-dimensional object minus the area of its base(s). It represents the sum of the areas of all the faces that are not bases. This measurement is commonly used when calculating the surface area of pyramids or objects with curved or rounded surfaces, such as cylinders, cones, and spheres.
`3`. Curved Surface Area
The curved surface area refers to the surface area of all the curved surfaces of a three-dimensional object. It takes into account the areas of all the curved faces and excludes the areas of the base(s). This measurement is commonly used when calculating the surface area of objects with curved or rounded surfaces, such as cylinders, cones, and spheres.
`4`. Total Surface Area
Total surface area refers to the sum of the areas of all surfaces covering the exterior of a three-dimensional object, including tha area of the base and the top. For example, for a cube or rectangular prism, the total surface area includes the areas of all six faces.

The surface area of a prism can be calculated by summing the areas of all its faces. In a prism two congruent polygons act as its bases and rectangular lateral faces connecting corresponding vertices of the bases. The formula for the surface area of a prism depends on the shape of its bases. Here are the general steps to find the surface area of a prism:
`1`. Find the area of the bases:
Calculate the area of one base of the prism. If the base is a regular polygon, you can use the appropriate formula for finding its area. If the base is irregular, you may need to use other methods such as decomposing it into simpler shapes or using Heron's formula for the area of a triangle . Multiply the base area by `2` to find the combined base area of the two bases.
`2`. Find the lateral area:
Calculate the lateral area of the prism, which is the combined area of all the rectangular faces. The lateral area can be found by multiplying the perimeter of one base by the height of the prism.
`3`. Add the base areas and the lateral area:
Once you have found the base area and the lateral area, add them together to get the total surface area of the prism.
Here are the specific formulas for finding the surface area of some common types of prisms:

The method for finding the surface area of an object depends on the shape of the object. The formula for calculating surface area changes with shape. For example:
- The surface area of a cube, cuboid, or rectangular prism is the sum of the areas of all six faces.
- The surface area of the sphere includes the area of all curved surfaces.
- Similarly, a cylinder that has two circular bases and one lateral surface would include the area of all these three surfaces.
Below are some common shapes and their corresponding methods for finding surface area:
`1`. Cube or Rectangular Prism:
To find the surface area of a rectangular prism, calculate the area of each of its faces (sides), and then sum them up.
\( \text{Surface Area} = 2lw + 2lh + 2wh \)
where \( l \), \( w \), and \( h \) are the lengths, widths, and heights of the rectangular prism.
For a cube all the sides are of equal length, and we can say \( l = w = h = s \).
Therefore, the formula simplifies to:
\( \text{Surface Area} = 2s^2 + 2s^2 + 2s^2 = 6s^2\)
Example: Find the surface area of a cube with side length \( s = 5 \) units.
Since a cube has all sides of equal length, we only need to calculate the area of one face and then multiply it by `6` to find its total surface area.
The formula for the total surface area of a cube is:
\( \text{Surface Area} = 6s^2 \)
Substitute the given side length \( s = 5 \) units:
\( \text{Surface Area} = 6 \times (5)^2 \)
\( \text{Surface Area} = 6 \times 25 \)
\( \text{Surface Area} = 150 \)
So, the surface area of the cube is \( 150 \) square units.
`2`. Sphere:
To find the surface area of a sphere, use the formula:
\( \text{Surface Area} = 4\pi r^2 \)
where \( r \) is the radius of the sphere.
Example: Find the surface area of a sphere with a radius \( r = 3 \) units.
We'll use the formula for the surface area of a sphere:
Substitute the given radius \( r = 3 \) units into the formula:
\( \text{Surface Area} = 4\pi \times (3)^2 \)
\( \text{Surface Area} = 4\pi \times 9 \)
\( \text{Surface Area} = 36\pi \)
So, the surface area of the sphere is \( 36\pi \) square units.
`3`. Cylinder:
To find the surface area of a cylinder, sum the areas of its two circular bases and its lateral surface area.
\( \text{Surface Area} = 2\pi r^2 + 2\pi rh \)
where \( r \) is the radius of the circular base and \( h \) is the height of the cylinder.
Example: Find the surface area of a cylinder with a radius \( r = 4 \) units and a height \( h = 6 \) units.
We'll use the formula for the surface area of a cylinder:
Substitute the given radius \( r = 4 \) units and height \( h = 6 \) units into the formula:
\( \text{Surface Area} = 2\pi (4)^2 + 2\pi (4)(6) \)
\( \text{Surface Area} = 2\pi \times 16 + 2\pi \times 24 \)
\( \text{Surface Area} = 32\pi + 48\pi \)
\( \text{Surface Area} = 80\pi \)
So, the surface area of the cylinder is \( 80\pi \) square units.
To find the surface area of a cone, add the area of its base and its lateral surface area.
\( \text{Surface Area} = \pi r^2 + \pi rl \)
where \( r \) is the radius of the circular base and \( l \) is the slant height of the cone.
Example: Find the surface area of a cone with a radius \( r = 3 \) units and a slant height \( l = 5 \) units.
We'll use the formula for the surface area of a cone:
Substitute the given radius \( r = 3 \) units and slant height \( l = 5 \) units into the formula:
\( \text{Surface Area} = \pi (3)^2 + \pi (3)(5) \)
\( \text{Surface Area} = \pi \times 9 + \pi \times 15 \)
\( \text{Surface Area} = 9\pi + 15\pi \)
\( \text{Surface Area} = 24\pi \)
So, the surface area of the cone is \( 24\pi \) square units.
`5`. Pyramid:
To find the surface area of a pyramid, sum the area of its base and the areas of its lateral faces.
\( \text{Surface Area} = \text{Base Area} + \text{Lateral Surface Area} \)
Example: Find the surface area of a square pyramid with a base side length \( s = 6 \) units and a slant height \( l = 8 \) units.
First, we need to find the area of the base of the pyramid, which is a square. Since all sides of a square are equal, the area of the base is given by \( \text{Base Area} = s^2 \).
Substitute the given side length \( s = 6 \) units into the formula:
\( \text{Base Area} = (6)^2 = 36 \text{ square units} \)
Now, we need to find the lateral surface area of the pyramid. Since it's a square pyramid, it has four identical triangular faces. The area of each triangular face can be calculated using the formula for the area of a triangle,
which is \( \frac{1}{2} \times \text{base} \times \text{height} \). Here, the base of each triangle is the side of the square base, which is \( s = 6 \) units, and the height is the slant height of the pyramid, which is \( l = 8 \) units.
\( \text{Area of one triangular face} = \frac{1}{2} \times 6 \times 8 = 24 \text{ square units} \)
Since there are four identical triangular faces, the total lateral surface area is:
\( \text{Lateral Surface Area} = 4 \times 24 = 96 \text{ square units} \)
Now, we can find the total surface area by summing the base area and the lateral surface area:
\( \text{Surface Area} = 36 + 96 = 132 \text{ square units} \)
So, the surface area of the square pyramid is \( 132 \) square units.
For more complex shapes, the process may involve decomposition into simpler shapes, using calculus techniques, or applying specialized formulas.
Real-life Applications of Surface Area Calculation
The surface area calculation has numerous real-life applications across various fields. Some examples include:
`1`. Construction and Architecture:
- Architects and engineers use surface area calculations to estimate the amount of materials needed for construction projects. For instance, they calculate the surface area of walls, floors, and roofs to determine the quantity of paint, tiles, or roofing materials required.
- Surface area calculations are crucial for determining the heat loss or gain through building envelopes, aiding in the design of energy-efficient buildings.
`2`. Packaging and Manufacturing:
- Manufacturers use surface area calculations to design packaging for products. Knowing the surface area helps optimize packaging dimensions to minimize material usage while ensuring adequate protection for the product.
- Surface area calculations are used in the design of various manufactured objects, such as containers, bottles, and cans, to optimize material usage and production costs.
`3`. Chemistry and Material Science:
- Surface area measurements play a vital role in characterizing porous materials, such as catalysts, adsorbents, and nanoparticles. Specific surface area calculations help determine the effectiveness of these materials in various chemical processes.
- In pharmaceuticals, surface area calculations are used to assess the dissolution rate of drugs, influencing their bioavailability and therapeutic efficacy.
`4`. Heat Transfer and Thermodynamics:
- Engineers use surface area calculations to analyze heat transfer processes, such as conduction, convection, and radiation. Surface area influences the rate at which heat is exchanged between objects and their surroundings.
- Surface area calculations are essential in designing heat exchangers, radiators, and cooling systems for applications ranging from HVAC systems to industrial processes.
`5`. Environmental Science and Biology:
- Biologists use surface area calculations to estimate the surface area of organisms, such as leaves, animal organs, and microorganisms. Surface area affects physiological processes like gas exchange, nutrient absorption, and heat dissipation.
- Environmental scientists use surface area calculations to assess the surface area of natural features, such as soil particles, aquatic sediments, and vegetation, influencing processes like chemical reactions, nutrient cycling, and habitat suitability.
Example `1`. Calculate the curved surface area of a cylinder with the following dimensions:
Radius (\( r \)) `= 2` cm
Height (\( h \)) `= 6` cm
Give your answer in terms of \( \pi \).
The lateral surface area \( A \) of a cylinder is given by the formula:
\( L.A = 2\pi rh \)
Substituting the given values:
\( L.A = 2\pi (2)(6) \)
\( L.A = 2\pi (12) \)
\( L.A = 324\pi \text{ square centimeters} \)
So, the surface area of the cylinder is \( 32\pi \, \text{cm}^2 \).
Example `2`. Calculate the surface area of a sphere with the following dimensions:
Radius (\( r \)) `= 3` cm
The surface area \( A \) of a sphere is given by the formula:
\( A = 4\pi r^2 \)
Substituting the given value:
\( A = 4\pi (3^2) \)
\( A = 4\pi (9) \)
\( A = 36\pi \text{ square centimeters} \)
So, the surface area of the sphere is \( 36\pi \, \text{cm}^2 \).
Example `3`. Calculate the surface area of a rectangular prism with the following dimensions:
Length (\( l \)) `= 4` cm
Width (\( w \)) `= 3` cm
Height (\( h \)) `= 5` cm
The surface area \( A \) of a rectangular prism is given by the formula:
\( A = 2lw + 2lh + 2wh \)
\( A = 2(4 \times 3) + 2(4 \times 5) + 2(3 \times 5) \)
\( A = 24 + 40 + 30 \)
\( A = 94 \text{ square centimeters} \)
So, the surface area of the rectangular prism is \( 94 \, \text{cm}^2 \).
Example `4`. Calculate the total surface area of a cone with the following dimensions:
Radius of the base (\( r \)) `= 4` cm
Slant height (\( l \)) `= 6` cm
The surface area \( A \) of a cone is given by the formula:
\( A = \pi r^2 + \pi rl \)
\( A = \pi (4^2) + \pi (4)(6) \)
\( A = \pi (16) + \pi (24) \)
\( A = 16\pi + 24\pi \)
\( A = 40\pi \text{ square centimeters} \)
So, the surface area of the cone is \( 40\pi \, \text{cm}^2 \).
Example `5`. Calculate the total surface area of a regular triangular prism with the following dimensions:
Base of the triangle (\( b \)) `= 6` cm
Height of the triangle (\( h \)) `= 8` cm
Length of the prism (\( l \)) `= 10` cm
The surface area \( A \) of a triangular prism is given by the formula:
\( A = \text{Base Area} + \text{Lateral Area} \)
First, let's find the base area:
\( \text{Base Area} = \frac{1}{2}bh = \frac{1}{2}(6)(8) = 24 \text{ square centimeters} \)
Next, let's find the lateral area:
The lateral faces are rectangles, so the lateral area is given by the perimeter of the base multiplied by the height of the prism.
\( \text{Lateral Area} = \text{Perimeter of the base} \times h = 3(6) \times 10 = 180 \text{ square centimeters} \)
Now, summing the base area and lateral area:
\( A = 24 + 180 = 204 \text{ square centimeters} \)
So, the surface area of the triangular prism is \( 204 \, \text{cm}^2 \).
Q`1`. Find the total surface area of a cube with the following dimensions:
Side length (\( s \)) `= 5` cm
- \( 150 \, \text{cm}^2 \)
- \( 25 \, \text{cm}^2 \)
- \( 50 \, \text{cm}^2 \)
- \( 100 \, \text{cm}^2 \)
Q`2`. Find the surface area of a sphere with radius (\( r \)) `= 4` cm. Give your answer in terms of \( \pi \).
- \( 32\pi \, \text{cm}^2 \)
- \( 64\pi \, \text{cm}^2 \)
- \( 16\pi \, \text{cm}^2 \)
- \( 64\pi \, \text{m}^2 \)
Q`3`. Find the lateral surface area of a rectangular prism with the following dimensions:
Length (\( l \)) `= 6` cm
Width (\( w \)) `= 4` cm
Height (\( h \)) `= 3` cm
- \( 72 \, \text{cm}^2 \)
- \( 108 \, \text{m}^2 \)
- \( 60 \, \text{cm}^2 \)
- \( 60 \, \text{cm}^3 \)
Q`4`. Find the curved surface area of a cylinder with the following dimensions:
Radius of the base (\( r \)) `= 5` cm
Height (\( h \)) `= 8` cm
- \( 40\pi \, \text{cm}^2 \)
- \( 130\pi \, \text{m}^2 \)
- \( 80\pi \, \text{cm}^2 \)
- \( 100\pi \, \text{cm}^2 \)
Q`5`. Calculate the total surface area of a cone with the following dimensions:
Radius of the base (\( r \)) `= 5` meters
Slant height (\( l \)) `= 12` meters
- \( 85\pi \, \text{m}^2 \)
- \( 60\pi \, \text{m}^2 \)
- \( 85\pi \, \text{cm}^2 \)
- \( 85\pi \, \text{m}^3 \)
Q`1`. What is surface area?
Answer: Surface area is the total area that covers the surface of a three-dimensional object. It includes the area of all faces of the object including the bottom and top faces.
Q`2`. Why is surface area important?
Answer: Surface area is important because it helps quantify the amount of material needed to cover or enclose an object. It is used in various fields such as construction, engineering, manufacturing, and science to optimize designs, estimate costs, and analyze physical properties.
Q`3`. How do you calculate the surface area of a shape?
Answer: The method for calculating surface area depends on the shape of the object. For common shapes like cubes, cylinders, spheres, and prisms, there are specific formulas to calculate their surface areas. These formulas involve finding the areas of individual faces and adding them together.
Q`4`. What are some real-life applications of surface area calculations?
Answer: Surface area calculations are used in construction to estimate material requirements for walls, floors, and roofs. They are also used in manufacturing to design packaging and optimize material usage. Additionally, surface area calculations play a role in fields such as chemistry, physics, and biology for analyzing heat transfer, characterizing materials, and understanding biological processes.
Q`5`. What is the difference between total surface area and lateral surface area?
Answer: Total surface area includes the areas of all faces of a three-dimensional object, including both the bases and the lateral faces. Lateral surface area, on the other hand, refers to the area of only the lateral (side) faces of an object, excluding the bases.
Q`6`. How does surface area affect heat transfer?
Answer: Surface area affects heat transfer by influencing the rate at which heat is exchanged between an object and its surroundings. Larger surface areas allow for more heat exchange, leading to faster heat transfer. This principle is utilized in various applications, such as in the design of heat exchangers and cooling systems.
Q`7`. Can the surface area be negative?
Answer: No, surface area cannot be negative. Surface area is a physical quantity representing the extent of the surface of an object, and it is always a non-negative value.
Algebra - Order Of Operations Algebra - Distributive Property `X` And `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant

Number Sense
Understanding numbers, their relationships and numerical reasoning
Using symbols to solve equations and express patterns

Studying shapes, sizes and spatial relationships in mathematics

Measurement
Quantifying and comparing attributes like length, weight and volume
Performing mathematical operations like addition, subtraction, division

Probability and Statistics
Analyzing uncertainty and likelihood of events and outcomes
Calculator Suite
Exploring functions, solving equations, constructing geometric shapes
Graphing Calculator
Visualizing equations and functions with interactive graphs and plots
Exploring geometric concepts and constructions in a dynamic environment
3D Calculator
Graphing functions and performing calculations in 3D
Scientific Calculator
Performing calculations with fractions, statistics and exponential functions
Exploring apps bundle including free tools for geometry, spreadsheet and CAS
Surface Area and Nets
Learn and practice finding the surface area of different types of solids with interactive resources from GeoGebra.
Middle School
Formulas for lateral surface area of solids.
Find the lateral area and surface area of a right prism, pyramid, right circular cylinder, and cone using formulas.
Exploration
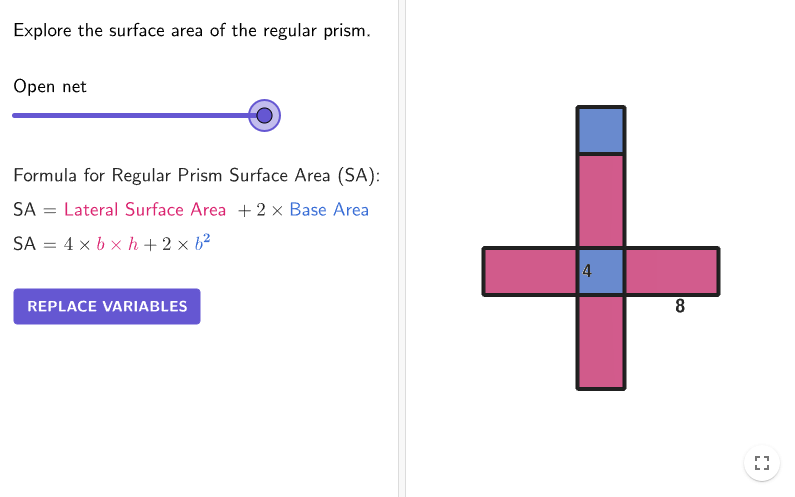
Surface Area Formula for Prisms
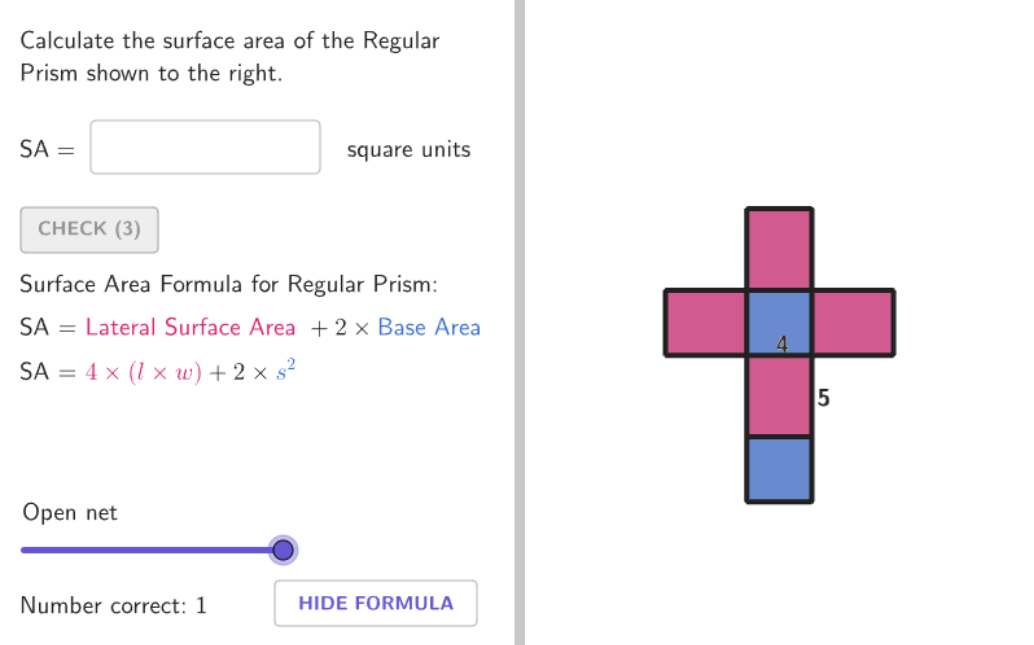
Using the Surface Area Formula for Regular Prisms

Surface Area Formula for Pyramids

Using the Surface Area Formula for Pyramids
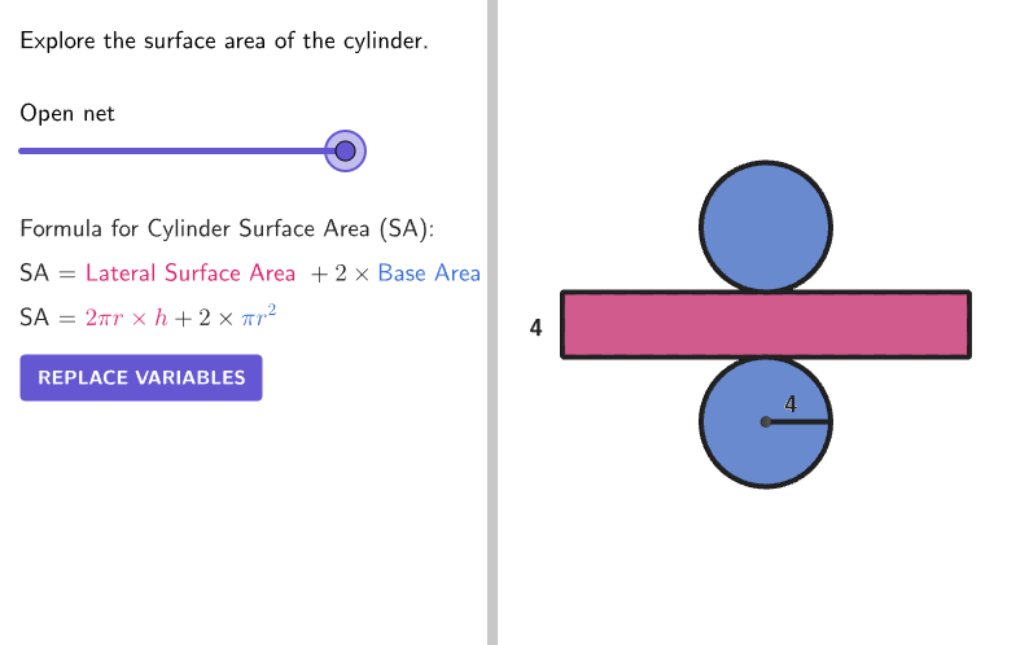
Surface Area Formula for Cylinders
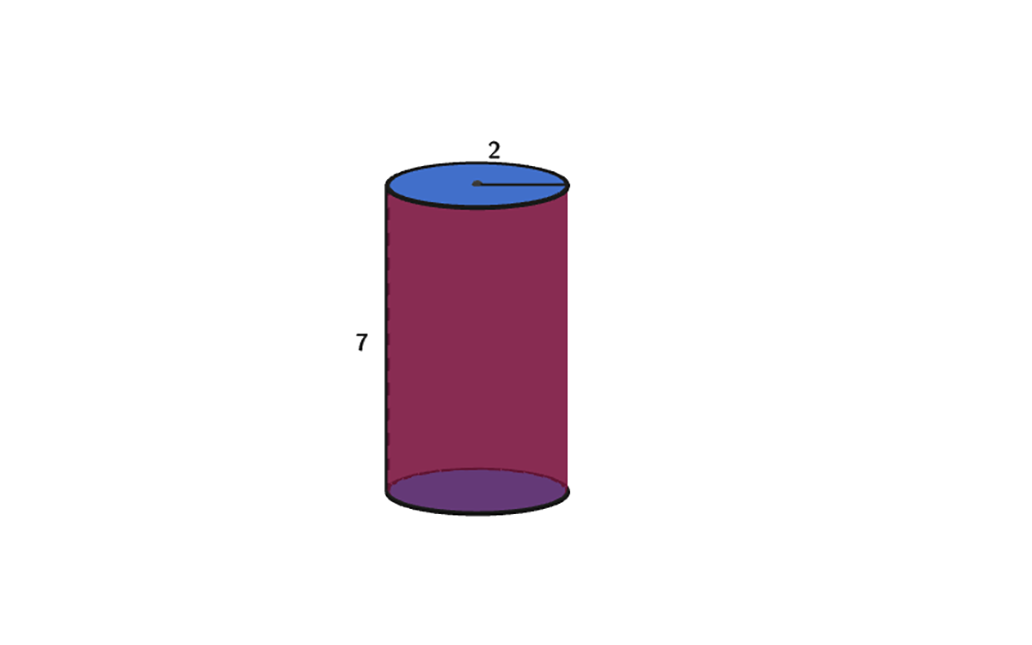
Using the Surface Area Formula for Cylinders

Surface Area Formula for Cone
Surface area of solids.
Use nets or formulas to find the surface area of prisms, pyramids, and cylinders in number and word problems.
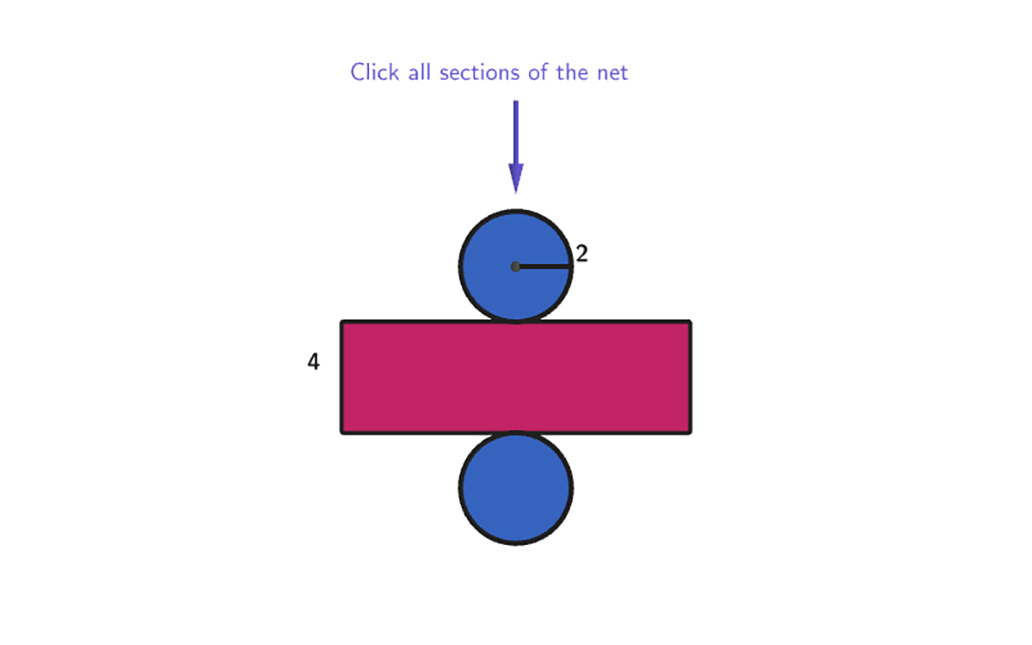
Calculating the Surface Area of Cylinders Using Nets
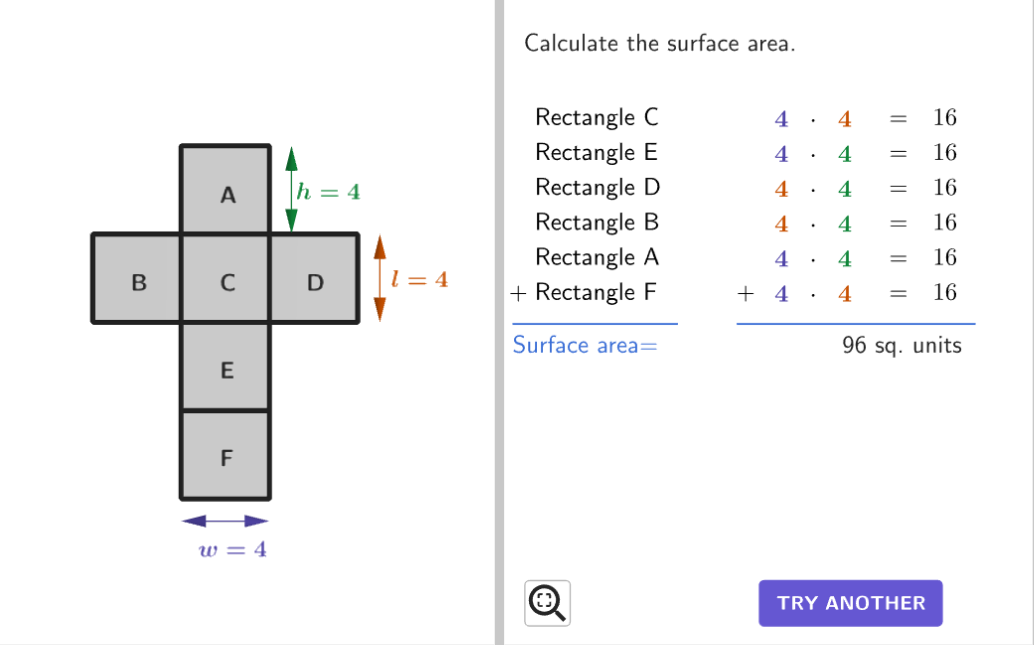
Calculating the Surface Area of Prisms Using Nets
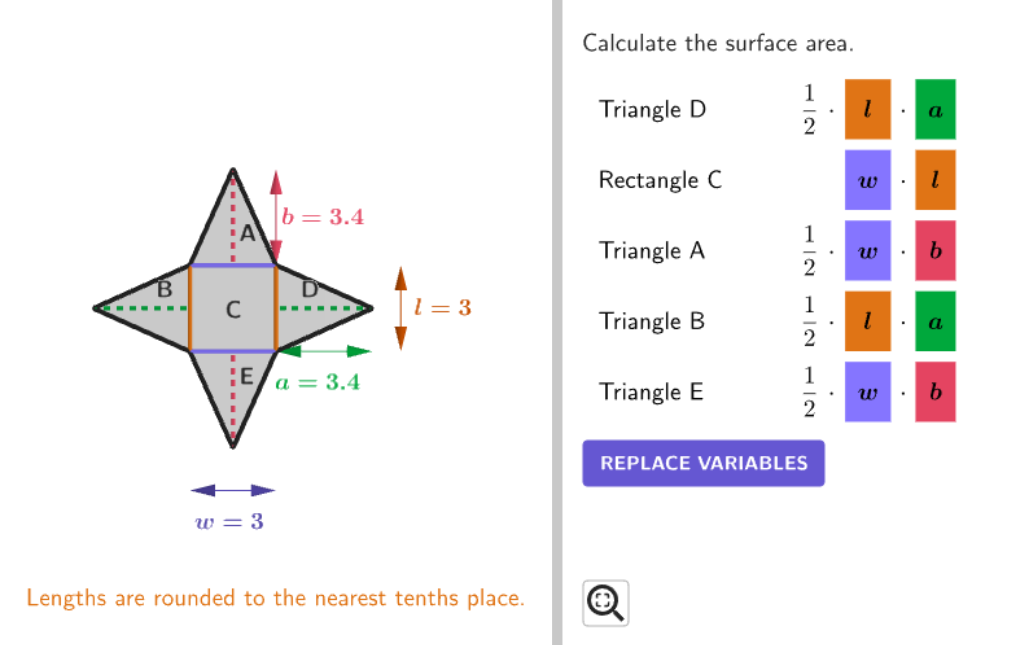
Calculating the Surface Area of Pyramids Using Nets
Related topics.
Congruence and Similarity
Perimeter and Circumference
Pythagoras' Theorem
Ratios and Rates
Units and Measurement
Community Resources
Explore an extensive collection of over one million math and science activities, exercises and lessons meticulously crafted by our global GeoGebra community. Immerse yourself in the boundless possibilities that await you.

Get started using GeoGebra today
Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others
9.6 Solve Geometry Applications: Volume and Surface Area
Learning objectives.
- Find volume and surface area of rectangular solids
- Find volume and surface area of spheres
- Find volume and surface area of cylinders
- Find volume of cones
Be Prepared 9.6
Before you get started, take this readiness quiz.
- Evaluate x 3 x 3 when x = 5 . x = 5 . If you missed this problem, review Example 2.15 .
- Evaluate 2 x 2 x when x = 5 . x = 5 . If you missed this problem, review Example 2.16 .
- Find the area of a circle with radius 7 2 . 7 2 . If you missed this problem, review Example 5.39 .
In this section, we will finish our study of geometry applications. We find the volume and surface area of some three-dimensional figures. Since we will be solving applications, we will once again show our Problem-Solving Strategy for Geometry Applications.
- Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
- Step 2. Identify what you are looking for.
- Step 3. Name what you are looking for. Choose a variable to represent that quantity.
- Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Step 5. Solve the equation using good algebra techniques.
- Step 6. Check the answer in the problem and make sure it makes sense.
- Step 7. Answer the question with a complete sentence.
Find Volume and Surface Area of Rectangular Solids
A cheerleading coach is having the squad paint wooden crates with the school colors to stand on at the games. (See Figure 9.28 ). The amount of paint needed to cover the outside of each box is the surface area , a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure.
Each crate is in the shape of a rectangular solid . Its dimensions are the length, width, and height. The rectangular solid shown in Figure 9.29 has length 4 4 units, width 2 2 units, and height 3 3 units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.
Altogether there are 24 24 cubic units. Notice that 24 24 is the length × width × height . length × width × height .
The volume, V , V , of any rectangular solid is the product of the length, width, and height.
We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, B , B , is equal to length × width . length × width .
We can substitute B B for L · W L · W in the volume formula to get another form of the volume formula.
We now have another version of the volume formula for rectangular solids. Let’s see how this works with the 4 × 2 × 3 4 × 2 × 3 rectangular solid we started with. See Figure 9.29 .
To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.
Notice for each of the three faces you see, there is an identical opposite face that does not show.
The surface area S S of the rectangular solid shown in Figure 9.30 is 52 52 square units.
In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see Figure 9.31 ). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side.
Volume and Surface Area of a Rectangular Solid
For a rectangular solid with length L , L , width W , W , and height H : H :
Manipulative Mathematics
Example 9.47.
For a rectangular solid with length 14 14 cm, height 17 17 cm, and width 9 9 cm, find the ⓐ volume and ⓑ surface area.
Step 1 is the same for both ⓐ and ⓑ , so we will show it just once.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the rectangular solid |
| Step 3. Choose a variable to represent it. | Let = volume |
| Step 4. Write the appropriate formula. Substitute. | |
| Step 5. the equation. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The volume is cubic centimeters. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the solid |
| Step 3. Choose a variable to represent it. | Let = surface area |
| Step 4. Write the appropriate formula. Substitute. | |
| Step 5. | |
| Step 6. Double-check with a calculator. | |
| Step 7. the question. | The surface area is 1,034 square centimeters. |
Try It 9.93
Find the ⓐ volume and ⓑ surface area of rectangular solid with the: length 8 8 feet, width 9 9 feet, and height 11 11 feet.
Try It 9.94
Find the ⓐ volume and ⓑ surface area of rectangular solid with the: length 15 15 feet, width 12 12 feet, and height 8 8 feet.
Example 9.48
A rectangular crate has a length of 30 30 inches, width of 25 25 inches, and height of 20 20 inches. Find its ⓐ volume and ⓑ surface area.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the crate |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. Substitute. | |
| Step 5. the equation. | |
| Step 6. Double check your math. | |
| Step 7. the question. | The volume is 15,000 cubic inches. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the crate |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. Substitute. | |
| Step 5. the equation. | |
| Step 6. Check it yourself! | |
| Step 7. the question. | The surface area is 3,700 square inches. |
Try It 9.95
A rectangular box has length 9 9 feet, width 4 4 feet, and height 6 6 feet. Find its ⓐ volume and ⓑ surface area.
Try It 9.96
A rectangular suitcase has length 22 22 inches, width 14 14 inches, and height 9 9 inches. Find its ⓐ volume and ⓑ surface area.
Volume and Surface Area of a Cube
A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:
So for a cube, the formulas for volume and surface area are V = s 3 V = s 3 and S = 6 s 2 . S = 6 s 2 .
For any cube with sides of length s , s ,
Example 9.49
A cube is 2.5 2.5 inches on each side. Find its ⓐ volume and ⓑ surface area.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the cube |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. | |
| Step 5. Substitute and solve. | |
| Step 6. Check your work. | |
| Step 7. the question. | The volume is 15.625 cubic inches. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the cube |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. | |
| Step 5. Substitute and solve. | |
| Step 6. The check is left to you. | |
| Step 7. the question. | The surface area is 37.5 square inches. |

Try It 9.97
For a cube with side 4.5 meters, find the ⓐ volume and ⓑ surface area of the cube.
Try It 9.98
For a cube with side 7.3 yards, find the ⓐ volume and ⓑ surface area of the cube.
Example 9.50
A notepad cube measures 2 2 inches on each side. Find its ⓐ volume and ⓑ surface area.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the cube |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. | |
| Step 5. the equation. | |
| Step 6. Check that you did the calculations correctly. | |
| Step 7. the question. | The volume is 8 cubic inches. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the cube |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. | |
| Step 5. the equation. | |
| Step 6. The check is left to you. | |
| Step 7. the question. | The surface area is 24 square inches. |
Try It 9.99
A packing box is a cube measuring 4 4 feet on each side. Find its ⓐ volume and ⓑ surface area.
Try It 9.100
A wall is made up of cube-shaped bricks. Each cube is 16 16 inches on each side. Find the ⓐ volume and ⓑ surface area of each cube.
Find the Volume and Surface Area of Spheres
A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.
Showing where these formulas come from, like we did for a rectangular solid, is beyond the scope of this course. We will approximate π π with 3.14 . 3.14 .
Volume and Surface Area of a Sphere
For a sphere with radius r : r :
Example 9.51
A sphere has a radius 6 6 inches. Find its ⓐ volume and ⓑ surface area.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the sphere |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. | |
| Step 5. | |
| Step 6. Double-check your math on a calculator. | |
| Step 7. the question. | The volume is approximately 904.32 cubic inches. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the cube |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. | |
| Step 5. | |
| Step 6. Double-check your math on a calculator | |
| Step 7. the question. | The surface area is approximately 452.16 square inches. |
Try It 9.101
Find the ⓐ volume and ⓑ surface area of a sphere with radius 3 centimeters.
Try It 9.102
Find the ⓐ volume and ⓑ surface area of each sphere with a radius of 1 1 foot
Example 9.52
A globe of Earth is in the shape of a sphere with radius 14 14 centimeters. Find its ⓐ volume and ⓑ surface area. Round the answer to the nearest hundredth.
| Step 1. the problem. Draw a figure with the given information and label it. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the sphere |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The volume is approximately 11,488.21 cubic inches. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the sphere |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The surface area is approximately 2461.76 square inches. |
Try It 9.103
A beach ball is in the shape of a sphere with radius of 9 9 inches. Find its ⓐ volume and ⓑ surface area.
Try It 9.104
A Roman statue depicts Atlas holding a globe with radius of 1.5 1.5 feet. Find the ⓐ volume and ⓑ surface area of the globe.
Find the Volume and Surface Area of a Cylinder
If you have ever seen a can of soda, you know what a cylinder looks like. A cylinder is a solid figure with two parallel circles of the same size at the top and bottom. The top and bottom of a cylinder are called the bases. The height h h of a cylinder is the distance between the two bases. For all the cylinders we will work with here, the sides and the height, h h , will be perpendicular to the bases.
Rectangular solids and cylinders are somewhat similar because they both have two bases and a height. The formula for the volume of a rectangular solid, V = B h V = B h , can also be used to find the volume of a cylinder.
For the rectangular solid, the area of the base, B B , is the area of the rectangular base, length × width. For a cylinder, the area of the base, B , B , is the area of its circular base, π r 2 . π r 2 . Figure 9.33 compares how the formula V = B h V = B h is used for rectangular solids and cylinders.
To understand the formula for the surface area of a cylinder, think of a can of vegetables. It has three surfaces: the top, the bottom, and the piece that forms the sides of the can. If you carefully cut the label off the side of the can and unroll it, you will see that it is a rectangle. See Figure 9.34 .
The distance around the edge of the can is the circumference of the cylinder’s base it is also the length L L of the rectangular label. The height of the cylinder is the width W W of the rectangular label. So the area of the label can be represented as
To find the total surface area of the cylinder, we add the areas of the two circles to the area of the rectangle.
The surface area of a cylinder with radius r r and height h , h , is
Volume and Surface Area of a Cylinder
For a cylinder with radius r r and height h : h :
Example 9.53
A cylinder has height 5 5 centimeters and radius 3 3 centimeters. Find the ⓐ volume and ⓑ surface area.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the cylinder |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The volume is approximately 141.3 cubic inches. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the cylinder |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The surface area is approximately 150.72 square inches. |
Try It 9.105
Find the ⓐ volume and ⓑ surface area of the cylinder with radius 4 cm and height 7cm.
Try It 9.106
Find the ⓐ volume and ⓑ surface area of the cylinder with given radius 2 ft and height 8 ft.
Example 9.54
Find the ⓐ volume and ⓑ surface area of a can of soda. The radius of the base is 4 4 centimeters and the height is 13 13 centimeters. Assume the can is shaped exactly like a cylinder.
| Step 1. the problem. Draw the figure and label it with the given information. |
| ⓐ | |
| Step 2. what you are looking for. | the volume of the cylinder |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check. | |
| Step 7. the question. | The volume is approximately 653.12 cubic centimeters. |
| ⓑ | |
| Step 2. what you are looking for. | the surface area of the cylinder |
| Step 3. Choose a variable to represent it. | let = surface area |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The surface area is approximately 427.04 square centimeters. |
Try It 9.107
Find the ⓐ volume and ⓑ surface area of a can of paint with radius 8 centimeters and height 19 centimeters. Assume the can is shaped exactly like a cylinder.
Try It 9.108
Find the ⓐ volume and ⓑ surface area of a cylindrical drum with radius 2.7 feet and height 4 feet. Assume the drum is shaped exactly like a cylinder.
Find the Volume of Cones
The first image that many of us have when we hear the word ‘cone’ is an ice cream cone. There are many other applications of cones (but most are not as tasty as ice cream cones). In this section, we will see how to find the volume of a cone.
In geometry, a cone is a solid figure with one circular base and a vertex. The height of a cone is the distance between its base and the vertex.The cones that we will look at in this section will always have the height perpendicular to the base. See Figure 9.35 .
Earlier in this section, we saw that the volume of a cylinder is V = π r 2 h . V = π r 2 h . We can think of a cone as part of a cylinder. Figure 9.36 shows a cone placed inside a cylinder with the same height and same base. If we compare the volume of the cone and the cylinder, we can see that the volume of the cone is less than that of the cylinder.
In fact, the volume of a cone is exactly one-third of the volume of a cylinder with the same base and height. The volume of a cone is
Since the base of a cone is a circle, we can substitute the formula of area of a circle, π r 2 π r 2 , for B B to get the formula for volume of a cone.
In this book, we will only find the volume of a cone, and not its surface area.
- Volume of a Cone
For a cone with radius r r and height h h .
Example 9.55
Find the volume of a cone with height 6 6 inches and radius of its base 2 2 inches.
| Step 1. the problem. Draw the figure and label it with the given information. | |
| Step 2. what you are looking for. | the volume of the cone |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for ) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The volume is approximately 25.12 cubic inches. |
Try It 9.109
Find the volume of a cone with height 7 7 inches and radius 3 3 inches
Try It 9.110
Find the volume of a cone with height 9 9 centimeters and radius 5 5 centimeters
Example 9.56
Marty’s favorite gastro pub serves french fries in a paper wrap shaped like a cone. What is the volume of a conic wrap that is 8 8 inches tall and 5 5 inches in diameter? Round the answer to the nearest hundredth.
| Step 1. the problem. Draw the figure and label it with the given information. Notice here that the base is the circle at the top of the cone. | |
| Step 2. what you are looking for. | the volume of the cone |
| Step 3. Choose a variable to represent it. | let = volume |
| Step 4. Write the appropriate formula. Substitute. (Use 3.14 for , and notice that we were given the distance across the circle, which is its diameter. The radius is 2.5 inches.) | |
| Step 5. | |
| Step 6. We leave it to you to check your calculations. | |
| Step 7. the question. | The volume of the wrap is approximately 52.33 cubic inches. |
Try It 9.111
How many cubic inches of candy will fit in a cone-shaped piñata that is 18 18 inches long and 12 12 inches across its base? Round the answer to the nearest hundredth.
Try It 9.112
What is the volume of a cone-shaped party hat that is 10 10 inches tall and 7 7 inches across at the base? Round the answer to the nearest hundredth.
Summary of Geometry Formulas
The following charts summarize all of the formulas covered in this chapter.
ACCESS ADDITIONAL ONLINE RESOURCES
Section 9.6 exercises, practice makes perfect.
In the following exercises, find ⓐ the volume and ⓑ the surface area of the rectangular solid with the given dimensions.
length 2 2 meters, width 1.5 1.5 meters, height 3 3 meters
length 5 5 feet, width 8 8 feet, height 2.5 2.5 feet
length 3.5 3.5 yards, width 2.1 2.1 yards, height 2.4 2.4 yards
length 8.8 8.8 centimeters, width 6.5 6.5 centimeters, height 4.2 4.2 centimeters
In the following exercises, solve.
Moving van A rectangular moving van has length 16 16 feet, width 8 8 feet, and height 8 8 feet. Find its ⓐ volume and ⓑ surface area.
Gift box A rectangular gift box has length 26 26 inches, width 16 16 inches, and height 4 4 inches. Find its ⓐ volume and ⓑ surface area.
Carton A rectangular carton has length 21.3 21.3 cm, width 24.2 24.2 cm, and height 6.5 6.5 cm. Find its ⓐ volume and ⓑ surface area.
Shipping container A rectangular shipping container has length 22.8 22.8 feet, width 8.5 8.5 feet, and height 8.2 8.2 feet. Find its ⓐ volume and ⓑ surface area.
In the following exercises, find ⓐ the volume and ⓑ the surface area of the cube with the given side length.
5 5 centimeters
10.4 10.4 feet
12.5 12.5 meters
Science center Each side of the cube at the Discovery Science Center in Santa Ana is 64 64 feet long. Find its ⓐ volume and ⓑ surface area.
Museum A cube-shaped museum has sides 45 45 meters long. Find its ⓐ volume and ⓑ surface area.
Base of statue The base of a statue is a cube with sides 2.8 2.8 meters long. Find its ⓐ volume and ⓑ surface area.
Tissue box A box of tissues is a cube with sides 4.5 inches long. Find its ⓐ volume and ⓑ surface area.
In the following exercises, find ⓐ the volume and ⓑ the surface area of the sphere with the given radius. Round answers to the nearest hundredth.
3 3 centimeters
7.5 7.5 feet
2.1 2.1 yards
In the following exercises, solve. Round answers to the nearest hundredth.
Exercise ball An exercise ball has a radius of 15 15 inches. Find its ⓐ volume and ⓑ surface area.
Balloon ride The Great Park Balloon is a big orange sphere with a radius of 36 36 feet . Find its ⓐ volume and ⓑ surface area.
Golf ball A golf ball has a radius of 4.5 4.5 centimeters. Find its ⓐ volume and ⓑ surface area.
Baseball A baseball has a radius of 2.9 2.9 inches. Find its ⓐ volume and ⓑ surface area.
In the following exercises, find ⓐ the volume and ⓑ the surface area of the cylinder with the given radius and height. Round answers to the nearest hundredth.
radius 3 3 feet, height 9 9 feet
radius 5 5 centimeters, height 15 15 centimeters
radius 1.5 1.5 meters, height 4.2 4.2 meters
radius 1.3 1.3 yards, height 2.8 2.8 yards
Coffee can A can of coffee has a radius of 5 5 cm and a height of 13 13 cm. Find its ⓐ volume and ⓑ surface area.
Snack pack A snack pack of cookies is shaped like a cylinder with radius 4 4 cm and height 3 3 cm. Find its ⓐ volume and ⓑ surface area.
Barber shop pole A cylindrical barber shop pole has a diameter of 6 6 inches and height of 24 24 inches. Find its ⓐ volume and ⓑ surface area.
Architecture A cylindrical column has a diameter of 8 8 feet and a height of 28 28 feet. Find its ⓐ volume and ⓑ surface area.
In the following exercises, find the volume of the cone with the given dimensions. Round answers to the nearest hundredth.
height 9 9 feet and radius 2 2 feet
height 8 8 inches and radius 6 6 inches
height 12.4 12.4 centimeters and radius 5 5 cm
height 15.2 15.2 meters and radius 4 4 meters
Teepee What is the volume of a cone-shaped teepee tent that is 10 10 feet tall and 10 10 feet across at the base?
Popcorn cup What is the volume of a cone-shaped popcorn cup that is 8 8 inches tall and 6 6 inches across at the base?
Silo What is the volume of a cone-shaped silo that is 50 50 feet tall and 70 70 feet across at the base?
Sand pile What is the volume of a cone-shaped pile of sand that is 12 12 meters tall and 30 30 meters across at the base?
Everyday Math
Street light post The post of a street light is shaped like a truncated cone, as shown in the picture below. It is a large cone minus a smaller top cone. The large cone is 30 30 feet tall with base radius 1 1 foot. The smaller cone is 10 10 feet tall with base radius of 0.5 0.5 feet. To the nearest tenth,
ⓐ find the volume of the large cone.
ⓑ find the volume of the small cone.
ⓒ find the volume of the post by subtracting the volume of the small cone from the volume of the large cone.
Ice cream cones A regular ice cream cone is 4 inches tall and has a diameter of 2.5 2.5 inches. A waffle cone is 7 7 inches tall and has a diameter of 3.25 3.25 inches. To the nearest hundredth,
ⓐ find the volume of the regular ice cream cone.
ⓑ find the volume of the waffle cone.
ⓒ how much more ice cream fits in the waffle cone compared to the regular cone?
Writing Exercises
The formulas for the volume of a cylinder and a cone are similar. Explain how you can remember which formula goes with which shape.
Which has a larger volume, a cube of sides of 8 8 feet or a sphere with a diameter of 8 8 feet? Explain your reasoning.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/prealgebra/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith
- Publisher/website: OpenStax
- Book title: Prealgebra
- Publication date: Sep 25, 2015
- Location: Houston, Texas
- Book URL: https://openstax.org/books/prealgebra/pages/1-introduction
- Section URL: https://openstax.org/books/prealgebra/pages/9-6-solve-geometry-applications-volume-and-surface-area
© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Reset password New user? Sign up
Existing user? Log in
Surface Area
Already have an account? Log in here.
- Pranshu Gaba
- Aditya Virani
- A Former Brilliant Member
- Lee Care Gene
The surface area of a three-dimensional object is the measure of the total area that the surface of the object occupies.
In this section, we will learn about the surface areas of various three-dimensional objects including cubes and spheres.
Surface Area of Common Figures
Example problems.
The surface area of a cube is the area of the six squares that cover it. The area of one of them is \(a \times a,\) or \(a^2 \). Since these are all the same, you can multiply one of them by six, so the surface area of a cube is 6 times one of the sides squared:
\[ (\text{Surface area of cube}) = 6 a^2 .\]
\[\] Rectangular Prisms
Rectangular Prism
The surface area of a rectangular prism is the area of the six rectangles that cover it. But we don't have to figure out all six because we know that the top and bottom are the same, the front and back are the same, and the left and right sides are the same.
As shown in the above diagram, the area of the top or the bottom with side lengths \(a\) and \(b\) is \(a\cdot b.\) Since there are two of them, we get \(2ab.\) The front and back have side lengths of \(a\) and \(c.\) The area of one of them is \(a\cdot c,\) and there are two of them, so the surface area of those two is \(2ac.\) The left and right sides have side lengths of \(b\) and \(c,\) so the surface area of one of them is \(b\cdot c.\) Again, there are two of them, so their combined surface area is \(2bc.\) Hence,
\[ \begin{align} (\text{Surface area of rectangular prism}) &= 2ab+2ac+2bc \\ &=2(ab+ac+bc ). \end{align} \]
Here are more problems on cuboid.
\[\] Triangular Prisms
Triangular Prism
If the top and bottom are regular triangles, the surface area of a triangular prism is the sum of the top and bottom areas and the area of the sides. Since there are both a top and a bottom which have the same area and that gets multiplied by two, \( \frac{\sqrt{3}}{4}a^2 \cdot 2 = \frac{\sqrt{3}}{2} a^2. \) Since each of the three sides has an area of \(a \cdot h ,\) the surface area of the sides is \( a \cdot h \times 3 = 3ah.\) Hence,
\[(\text{Surface area of a triangular prism}) = \frac{\sqrt{3}}{2} a^2 + 3ah. \]
\[\] Surface Area of Cylinders
The surface area of a cylinder is the sum of the area of the top and bottom and the area of the side.
Since there are both a top and a bottom and that gets multiplied by two, their area is
\[ \pi r^2 \times 2 = 2\pi r^2 .\]
If the side of cylinder lays flat, the surface area of the side is the same as the area of a rectangle where one side is the height of the cylinder and the other side is the perimeter of the circle, i.e. \( 2 \pi r \times h = 2\pi r h .\) Hence,
\[ (\text{Surface area of cylinder}) = 2\pi r^2 + 2 \pi r h. \]
Here are more problems on cylinder.
\[\] Surface Area of any Right Prism
A Right Prism
The surface area of any right prism is the sum of the area of the top and bottom and area of the side. If we let the area of the top or bottom be \(S,\) then the surface area of the top and bottom is \(2S.\) If we let \(L\) be the perimeter of top and bottom, then the surface area of the side is \( L \times h.\) Hence,
\[ (\text{Surface area of any right prism}) = 2S + L h.\]
\[\] Surface Area of Spheres
The surface area of a sphere is \( 4 \pi r^2, \) which is the same as the area of a circle whose radius is \(2r.\)
Here are more problems on sphere.
What is the surface area of a cube whose side length is 5? Since a cube has six squares, the surface area of a cube which has side length 5 is \[ 5^2 \times 6 = 150. \ _\square \]
What is the surface area of a sphere whose radius is 3? Since the formula for the surface area of a sphere is \( 4 \pi r^2, \) the surface area of a sphere with radius 3 is \[ 4\pi\cdot {3}^{2} = 36 \pi. \ _\square \]
What is the surface area of a prism in which the areas of the top and bottom are each 5, the perimeters of the top and bottom are each 9, and the height is 10? The surface of a prism consists of top, bottom, and sides. Since the surface areas of the top and bottom are each 5 and the surface area of the side is \(9\times 10=90,\) the surface area of the prism is \[ 2 \times 5 + 90 = 100. \ _\square\]
What is surface area of a rectangular prism whose side lengths are \(3,2,5?\) The surface area of a rectangular prism which has side lengths \(3,2,5\) is \[ 2(3\cdot 2 + 3\cdot 5 + 2 \cdot 5) = 62. \ _\square\]
The diagram to the right shows a cube sliced in half.
Find the total surface area of the sliced cube to the nearest integer.
Problem Loading...
Note Loading...
Set Loading...
SOLVING SURFACE AREA PROBLEMS
We may need to find surface area of different figures to solve many real-world problems.
In this section, we are going to see, how surface area of figures can be used to solve real world problems.
Let us see, how to find surface area of a prism.

Example 1 :
Erin is making a jewelry box of wood in the shape of a rectangular prism. The jewelry box will have the dimensions shown below. The cost of painting the exterior of the box is $0.50 per square in. How much does Erin have to spend to paint the jewelry box ?
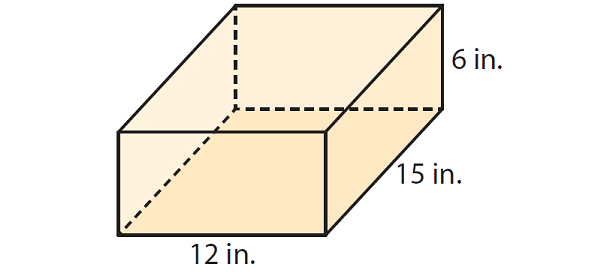
Solution :
To know that total cost of painting, first we have to know the Surface area of the jewelry box.
Find surface area of the box.
Identify a base, and find its area and perimeter.
Any pair of opposite faces can be the bases. For example, we can choose the bottom and top of the box as the bases.
Find base area.
B = l x w
B = 12 x 15
B = 180 square in.
Find perimeter of the base.
P = 2(12) + 2(15)
P = 24 + 30
P = 54 in.
Step 2 :
Identify the height, and find the surface area.
The height h of the prism is 6 inches. Use the formula to find the surface area.
S = Ph + 2B
S = 54(6) + 2(180)
S = 684 square inches
Total cost = Area x Cost per square in.
Total cost = 684 x $0.50
Total cost = $342
So, Erin has to spend $342 to paint the jewelry box.
Example 2 :
A metal box that is in the shape of rectangular prism has the following dimensions. The length is 9 inches, width is 2 inches, and height is 1 1/ 2 inches. Find the total cost of silver coating for the entire box.
To know that total cost of silver coating, first we have to know the Surface area of the metal box.
B = 9 x 2
B = 18 square in.
P = 2(9) + 2(2)
P = 18 + 4
P = 22 in.
The height h of the prism is 1 1/2 inches. Use the formula to find the surface area.
S = 22(1 1/2) + 2(18)
S = 22(3/2) + 36
S = 33 + 36
S = 69 square inches
Total cost = 69 x $1.50
Total cost = $103.50
So, the total cost of silver coating for the entire box is $103.50.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Digital sat math problems and solutions (part - 36).
Aug 30, 24 02:32 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Aug 30, 24 02:16 AM
Solving Exponential Equations Problems and Solutions (Part - 3)
Aug 30, 24 01:55 AM
Surface Area and Volume Questions

Surface Area and Volume Questions are available with answers here. Class 10 students can practise the questions based on surface area and volumes to prepare for the exams. These surface area and volume problems are prepared by our subject experts, as per the NCERT curriculum and latest CBSE syllabus (2022-2023). Learn more: Surface Areas and Volume .
Surface Area and Volume Formulas:
- Total surface area of a cuboid = 2[lb + bh + lh]
- Total surface area of a cube = 6(side) 2
- Lateral surface area of a cuboid = Area of walls of a room = 2(l + b) × h
- Lateral surface area of a cube = 4a 2
- Curved surface area of cylinder = 2πrh
- Total surface area of a cylinder = 2πr(r + h)
- Curved surface area of a cone = πrl
- Total surface area of a cone = πr(r + l)
- Surface area of a sphere = 4πr 2
- Curved surface area of a hemisphere = 2πr 2
- Total surface area of a hemisphere = 3πr 2
- Volume of a cuboid = l × b × h
- Volume of a cube = (side) 3
- Volume of a cylinder = πr 2 h
- Volume of a cone = ⅓ πr 2 h
Volume of a sphere = 4/3 πr 3
- Volume of a hemisphere = ⅔ πr 3
Surface Area and Volume Questions and Solutions
Q.1: If the radius of a sphere is 3r, what is its volume?
Solution: Given,
Radius of sphere = 3r
= 4/3 π(3r) 3 (given)
= 4/3 π27r 3
= 36πr 3 cu.units.
Q.2: What is the total surface area of a cuboid whose length = 5 cm, width = 2 cm and height = 3 cm?
Solution: Given, the dimensions of cuboid are:
Length, l = 5 cm
Width, w = 2 cm
Height, h = 3 cm
Surface area of cuboid = 2(lb + bh + lh)
= 2 (5.2 + 2.3 + 3.5)
= 2 (10 + 6 + 15)
= 62 sq.cm.
Q.3: If the radius of a sphere is doubled, find the ratio of their volumes.
Solution: Let the radius of a sphere is r.
Volume of a sphere, V1 = 4/3 πr 3
New radius = 2r
New volume, V2 = 4/3 π(2r) 3 = 4/3 π.2 3 r 3
Ratio of volumes = V1/V2
= (4/3 πr 3 )/(4/3 π.2 3 r 3 )
Hence, 1:8 is the required volume ratio.
Q.4: Two cubes of edge 6 cm are joined to form a cuboid. Find the total surface area of the cuboid.
When two cubes are joined end to end, then;
Length of the cuboid = 6 + 6 = 12 cm
Breadth of the cuboid = 6 cm
Height of the cuboid = 6 cm
Total surface area of the cuboid = 2 (lb + bh + hi)
= 2(12 x 6 + 6 × 6 + 6 ×12)
= 2(72 + 36 + 72) = 2(180) = 360 cm 2
Q.5: Find the area of the sheet required to make a closed cylindrical vessel of height 1 m and diameter 140 cm.
Height of cylindrical vessel = 1m
Diameter = 140 cm
Radius = 140/2 = 70 cm = 0.7 m
Total surface area of the closed cylindrical tank = 2 π r (r + h)
= 2 × 22/7 × 0.7 m × (0.7 m + 1 m)
= 4.4 m × 1.7 m
Hence, 7.48 m² of the sheet is required.
Q.6: A 5m wide cloth is used to make a conical tent of base diameter 14m and height 24m. Find the cost of cloth used at the rate of Rs. 25 per metre.
Height of tent, h = 24 m
Diameter = 14 m, radius, r = 7m
Slant height, l = √(h 2 + r 2 ) = √(24 2 + 7 2 ) = √625 = 25 m
Curved surface area of cone = πrl
= 22/7 x 7 x 25
Length of cloth = Area/width of cloth
Cost of cloth per meter = Rs.25
Therefore, total cost of cloth used = 25 x 110 = Rs. 2750/-
Q.7: 30 circular plates, each of radius 14 cm and thickness 3 cm are placed one above the other to form a cylindrical solid. Find the total surface area.
Solution: Given, radius 14 cm, thickness =3 cm, number of plates =30
Therefore, the height of cylinder will be 3×30=90 cm
We know, total surface area of cylinder =2πr(r+h) cm2
Therefore, total surface area =2π(14)(14+(90))=9152 cm2
Q.8: The outer and the inner radii of a hollow sphere are 12 cm and 10 cm. Find its volume.
Inner radius of hollow sphere (r) = 10 cm
Outer radius of hollow sphere (R) = 12 cm
Volume of sphere = 4/3 π (R 3 – r 3 )
= 4/3 x 22/7 (12 3 – 10 3 )
= 4/3 x 22/7 (1728 – 1000)
= 4/3 x 22/7 x 728
= 3050.67 cm 3
Q.9: The radius of the base of a right circular cylinder is 3 cm and height is 7 cm. Find the curved surface area.
Radius of cylinder, r=3 cm
Height of cylinder, h=7 cm
Curved Surface Area of a Cylinder =2πrh
CSA = 2 x 22/7 x 3 x 7 = 132 sq.cm.
Q.10: A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height?
Solution: Let the radius of sphere be r
Height of right circular cylinder be h
According to the question;
4/3 πr 3 = πr 2 h
Diameter of cylinder = 2 x r = 2(¾ h) = 3/2 h
Increase in height = (3/2 – 1)h = ½ h
Therefore, the required percentage is:
(½ h)/h x 100
Related Articles
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Skills by Standard
- Skills by Grade
- Skills by Category
Go to profile
- Assignments
- Assessments
- Report Cards
- Our Teachers
Remove ads and gain access to the arcade and premium games!
Unlock harder levels by getting an average of 80% or higher.
Earn up to 5 stars for each level The more questions you answer correctly, the more stars you'll unlock!
Each game has 10 questions. Green box means correct. Yellow box means incorrect.
Need some help or instruction on how to do this skill?
Want a paper copy? Print a generated PDF for this skill.
Share MathGames with your students, and track their progress.
See how you scored compared to other students from around the world.
Learn Math Together.
Grade 7 - Geometry
Standard 7.G.B.6 - Calculate the surface area of cubes and rectangular prisms.
Included Skills:
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
If you notice any problems, please let us know .

Surface Area of Cylinders Practice Questions
Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
- Problems on Pyramid
Solved word problems on pyramid are shown below using step-by-step explanation with the help of the exact diagram in finding surface area and volume of a pyramid.
Worked-out problems on pyramid: 1. The base of a right pyramid is a square of side 24 cm. and its height is 16 cm.
(i) the area of its slant surface
(ii) area of its whole surface and
(iii) its volume.
Let, the square WXYZ be the base of the right pyramid and its diagonals WY and XZ intersect at O. If OP be perpendicular to the plane of the square at O, then OP is the height of the pyramid.
Draw OE ┴ WX Then, E is the mid - point of WX .
By question, OP = 16 cm. and WX = 24 cm. Therefore, OE = EX = 1/2 ∙ WX = 12 cm Clearly, PE is the slant height of the pyramid. Since OP ┴ OE , hence from ∆ POE we get, PE² = OP² + OE²
or,PE² = 16² + 12²
or, PE² = 256 + 144
or, PE² = 400
PE = √400
Therefore, PE = 20. Therefore, (i) the required area of slant surface of the right pyramid
= 1/2 × perimeter of the base × slant height.
= 1/2 × 4 × 24× 20 square cm.
= 960 square cm.
(ii) The area of the whole surface of the right pyramid = area of slant surface + area of the base
= (960 + 24 × 24) square cm
= 1536 square cm.
(iii) the volume of the right pyramid
= 1/3 × area of the base × height
= 1/3 × 24 × 24 × 16 cubic cm
= 3072 cubic cm.
2. The base of a right pyramid 8 m high, is an equilateral triangle of side 12√3 m. Find its volume and the slant surface. Solution:
Let equilateral ∆ WXY be the base and P, the vertex of the right pyramid.
In the plane of the ∆ WXY draw YZ perpendicular to WX and let OZ = 1/3 YZ . Then, O is the centroid of ∆ WXY. Let OP be perpendicular to the plane of ∆ WXY at O; then OP is the height of the pyramid. By question, WX = XY = YW = 8√3 m and OP = 8 m. Since ∆ WXY is equilateral and YZ ┴ WX Hence, Z bisects WX .
Therefore, XZ = 1/2 ∙ WX = 1/2 ∙ 12√3 = 6√3 m. Now, from right - angled ∆ XYZ we get,
YZ² = XY² - XZ²
or, YZ² = (12√3) ² - (6√3)²
or, YZ² = 6² (12 - 3)
or, YZ² = 6² ∙ 9
or, YZ² = 324
Therefore, YZ = 18
Therefore, OZ = 1/3 ∙ 18 = 6. Join PZ . Then, PZ is the slant height of the pyramid. Since OP is perpendicular to the plane of ∆ WXY at O, hence OP ┴ OZ . Therefore, from the right angled ∆ POZ we get,
PZ² = OZ² + OP²
or, PZ ² = 6² + 8²
or, PZ² = 36 + 64
or, PZ² = 100
Therefore, PZ = 10 Therefore, the required slant surface of the right pyramid
= 1/2 × perimetre of the base × slant height
= 1/2 × 3 × 12√3 × PZ
= 1/2 × 36√3 × 10
= 180√3 square meter.
and its volume = 1/3 × area of the base × height
= 1/3 × (√3)/4 (12√3)² × 8
[Since, area of equilateral triangle
= (√3)/4 × (length of a side)² and height = OP = 8]
= 288√3 cubic meter.
● Mensuration
- Formulas for 3D Shapes
- Volume and Surface Area of the Prism
- Worksheet on Volume and Surface Area of Prism
- Volume and Whole Surface Area of Right Pyramid
- Volume and Whole Surface Area of Tetrahedron
- Volume of a Pyramid
- Volume and Surface Area of a Pyramid
- Worksheet on Volume and Surface Area of a Pyramid
- Worksheet on Volume of a Pyramid
11 and 12 Grade Math From Problems on Pyramid to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Worksheet on bar graphs | bar graphs or column graphs | graphing bar.
Aug 30, 24 02:28 AM
Worksheet on Data Handling | Questions on Handling Data |Grouping Data
Aug 30, 24 02:11 AM
Data Handling | Data Analysis | Data Processing | Numerical Data | Def
Aug 30, 24 12:28 AM
Construction of Bar Graphs | Examples on Construction of Column Graph
Aug 29, 24 11:56 PM
5th Grade Bar Graph | Definition | Interpret Bar Graphs|Free Worksheet
Aug 29, 24 02:11 AM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Surface Area of a Cube
In these lessons, we will learn
- how to calculate the surface area of a cube.
- how to find the length of a cube given the surface area.
- how to use the net of a cube to find its surface area.
- how to find the surface area of a cube in terms of its volume.
Related Pages Surface Area Formula Surface Area of Prisms Surface Area of a Sphere More Geometry Lessons
A cube is a three-dimensional figure with six equal square faces. The surface area of a cube is the sum of the area of the six squares that cover it.
The following figure shows the surface area of a cube. Scroll down the page for more examples and solutions of finding the surface area of a cube.
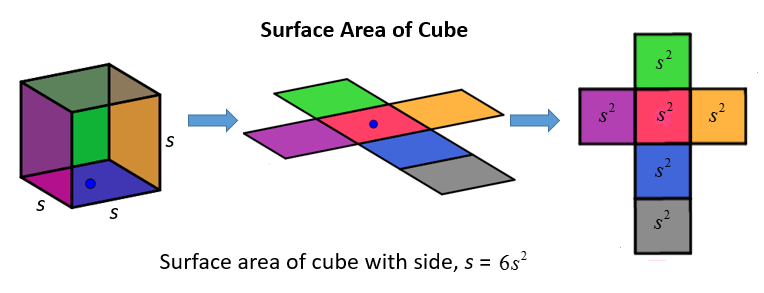
If s is the length of one of its sides, then the area of one face of the cube is s 2 .
Since a cube has six faces the surface area of a cube is six times the area of one face.
Surface area of a cube = 6 s 2
Worksheet to calculate volume and surface area of cubes
Example: Find the surface area of a cube with a side of length 3 cm
Solution: Given that s = 3
Surface area of a cube = 6 s 2 = 6(3) 2 = 54 cm 2
How to find the surface area of a cube?
Example: Given a side of 3 cm, find the surface area of the cube.
** How to find the surface area of a cube?** Step 1: Find the length of a side Step 2: Substitute into the formula: side × side × 6 and evaluate Step 3: Write the units
How to find the length of a cube given the surface area? This video shows how to find the length of a cube given the surface area. Example: The total surface area of a cube is 216 in 2 . What is the length of each side of the cube?
How to use the net of a cube to find its surface area? Another way to look at the surface area of a cube is to consider a net of the cube. The net is a 2-dimensional figure that can be folded to form a 3-dimensional object.
Imagine making cuts along some edges of a cube and opening it up to form a plane figure. The plane figure is called the net of the cube.
The following net can be folded along the dotted lines to form a cube.
We can then calculate the area of each square in the net and then multiply the area by 6 to get the surface area of the cube.
There are altogether 11 possible nets for a cube as shown in the following figures. Notice that the surface area of each of the net is the same.
How to use nets and 3-dimensional figures to find surface area of cubes and prisms?
Surface Area of a Cube in terms of its Volume How to find the surface area of a cube in terms of volume S = 6V 2/3

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Surface area
This article is a stub. Help us out by expanding it .
The surface area of a solid is the total exposed area that it has. For example, the surface area of a cube is the sum of the areas of its six square faces ; the surface area of a tetrahedron is the sum of the area of its four triangular faces. In general, for any polyhedron without holes, the surface area is just the sum of the areas of the faces of the polyhedron. Some other solids, such as the cylinder and right cone , have surface areas that can be computed relatively easily. However, for most solids, calculus is necessary to compute the surface area.
Something appears to not have loaded correctly.
Click to refresh .

IMAGES
VIDEO
COMMENTS
Example 6: surface area of a square pyramid - word problem. Mara is making a square pyramid out of cardboard. ... a mixture of solving for the missing surface area versus a missing dimension, and one that includes some word problems. Easy mistakes to make. Calculating volume instead of surface area
Lesson 12.4 Real-World Problems: Surface Area and Volume 201 L e a r n Solve word problems about surface area and volume of non-rectangular prisms. A block of wood is a prism and has the dimensions shown in the diagram below. a) Find the volume of the block of wood. 3 cm 3 cm 4 cm 4 cm 7 cm 5 cm The base of the prism is a trapezoid.
Math: Pre-K - 8th grade; Pre-K through grade 2 (Khan Kids) Early math review; 2nd grade; 3rd grade; 4th grade; 5th grade; 6th grade; 7th grade; 8th grade; See Pre-K - 8th Math; ... If this problem persists, tell us. Our mission is to provide a free, world-class education to anyone, anywhere.
The surface area is a square measure of the total area of all the sides of a rectangular solid. The amount of space inside the rectangular solid is the volume, a cubic measure. ... Problem Solving Strategy for Geometry Applications. Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with ...
Surface area worksheets comprise an enormous collection of exercises on different solid figures. The large chunk of exercises is categorized based on a step-by-step approach involving counting unit squares to determine the SA, finding the surface area of nets, and then computing the surface area of geometrical shapes like cubes, cones, cylinders, rectangular prisms, L-shaped prisms, spheres ...
Surface Area = 2 π r 2 + 2 π r h. where r is the radius of the circular base and h is the height of the cylinder. Example: Find the surface area of a cylinder with a radius r = 4 units and a height h = 6 units. Solution: We'll use the formula for the surface area of a cylinder: Surface Area = 2 π r 2 + 2 π r h.
Click here for Questions and Answers. Surface Area of a Cylinder. Click here for Questions and Answers. Surface Area of a Sphere. Click here for Questions and Answers. Surface Area of a Cone. Click here for Questions and Answers. Practice Questions. Previous: Surface Area Videos.
Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others. Discover 10 free and ready-to-use GeoGebra resources for grades 4-8 to practice finding the surface area of solids including prisms, pyramids, and cylinders in real-world math problems.
The surface area S S of the rectangular solid shown in Figure 9.30 is 52 52 square units. In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see Figure 9.31). Find the area of each face that you see and then multiply each area by two to ...
The surface area of a cube is the area of the six squares that cover it. The area of one of them is a \times a, a×a, or a^2 a2. Since these are all the same, you can multiply one of them by six, so the surface area of a cube is 6 times one of the sides squared: (\text {Surface area of cube}) = 6 a^2 . (Surface area of cube) = 6a2.
Practice and Problem Solving: A/B 1. 142 in2 2. 190 cm2 3. 1,236 cm2 4. 3,380 ft2 5. Possible answer: I would find the total surface area of each cube and then subtract the area of the sides that are not painted, including the square underneath the small cube. 6. 384 in2 Practice and Problem Solving: C 1. 101.4 in2 2. 797.4 m2 3. Check students ...
Problem 2 : A metal box that is in the shape of rectangular prism has the following dimensions. The length is 9 inches, width is 2 inches, and height is 1 1/ 2 inches. Find the total cost of silver coating for the entire box. Solution : To know that total cost of silver coating, first we have to know the Surface area of the metal box. Find ...
To know that total cost of silver coating, first we have to know the Surface area of the metal box. Find surface area of the box. Step 1 : Identify a base, and find its area and perimeter. Any pair of opposite faces can be the bases. For example, we can choose the bottom and top of the box as the bases. Find base area. B = l x w. B = 9 x 2
Solve application problems involving surface area and volume. Volume and surface area are two measurements that are part of our daily lives. We use volume every day, even though we do not focus on it. When you purchase groceries, volume is the key to pricing. Judging how much paint to buy or how many square feet of siding to purchase is based ...
Surface area of a sphere = 4πr 2. Curved surface area of a hemisphere = 2πr 2. Total surface area of a hemisphere = 3πr 2. Volume of a cuboid = l × b × h. Volume of a cube = (side) 3. Volume of a cylinder = πr 2 h. Volume of a cone = ⅓ πr 2 h. Volume of a sphere = 4/3 πr 3. Volume of a hemisphere = ⅔ πr 3.
Standard 7.G.B.6 - Calculate the surface area of cubes and rectangular prisms. Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms. If you notice any problems, please let us know.
To find the total surface area of the cylinder, we add the areas of the two circles to the area of the rectangle. The surface area of a cylinder with radius r and height h, is. S = 2πr2 + 2πrh (9.6.16) (9.6.16) S = 2 π r 2 + 2 π r h. Definition: Volume and Surface Area of a Cylinder.
Do you need a copy of the book? Here is the regular 7th grade book: https://amzn.to/3h5ev48Here is the accelerated 7th grade book: https://amzn.to/2VqfdRS
The Corbettmaths Practice Questions on Surface Area of a Cylinder. Previous: Surface Area of a Cone Practice Questions
Solved word problems on pyramid are shown below using step-by-step explanation with the help of the exact diagram in finding surface area and volume of a pyramid. Worked-out problems on pyramid: 1. The base of a right pyramid is a square of side 24 cm. and its height is 16 cm. Find: (i) the area of its slant surface (ii) area of its whole ...
If s is the length of one of its sides, then the area of one face of the cube is s2. Since a cube has six faces the surface area of a cube is six times the area of one face. Surface area of a cube = 6 s2. Worksheet to calculate volume and surface area of cubes. Surface area of a cube = 6 s2 = 6 (3) 2 = 54 cm 2.
The surface area of a solid is the total exposed area that it has. For example, the surface area of a cube is the sum of the areas of its six square faces; the surface area of a tetrahedron is the sum of the area of its four triangular faces. In general, for any polyhedron without holes, the surface area is just the sum of the areas of the ...
Certain cookies and other technologies are essential in order to enable our Service to provide the features you have requested, such as making it possible for you to access our product and information related to your account.