
Andrew W. Appel , Princeton University
David Bindel , Cornell University
Jean-Baptiste Jeannin , University of Michigan
Karthik Duraisamy , University of Michigan
Ariel Kellison , Cornell University, PhD Student
Josh Cohen , Princeton University, PhD Student
Yichen Tao , Sahil Bola , University of Michigan, PhD Students
Shengyi Wang , Princeton University, Research Scientist
Mohit Tekriwal , Lawrence Livermore Lab, Postdoc, External Collaborator
Philip Johnson-Freyd, Samuel Pollard , Heidi Thornquist , Sandia National Labs, External Collaborators
In this collection of research projects, we take a layered approach to foundational verification of correctness and accuracy of numerical software–that is, formal machine-checked proofs about programs (not just algorithms), with no assumptions except specifications of instruction-set architectures. We build, improve, and use appropriate tools at each layer: proving in the real numbers about discrete algorithms; proving how floating-point algorithms approximate real-number algorithms; reasoning about C program implementation of floating-point algorithms; and connecting all proofs end-to-end in Coq.
Our initial research projects (and results) are,
- cbench_vst /sqrt: Square root by Newton’s Method, by Appel and Bertot .
- VerifiedLeapfrog : A verified numerical method for an Ordinary Differential Equation, by Kellison and Appel .
- VCFloat2 : Floating-point error analysis in Coq, by Appel & Kellison, improvements on an earlier open-source project by Ramananandro et al.
- Parallel Dot Product , demonstrating how to use VST to verify correctness of simple shared-memory task parallelism
- Stationary Iterative Methods with formally verified error bounds

Bibliography
- Verified correctness, accuracy, and convergence of a stationary iterative linear solver: Jacobi method , by Mohit Tekriwal, Andrew W. Appel, Ariel E. Kellison, David Bindel, and Jean-Baptiste Jeannin. 16th Conference on Intelligent Computer Mathematics , September 2023.
- LAProof: a library of formal accuracy and correctness proofs for sparse linear algebra programs , by Ariel E. Kellison, Andrew W. Appel, Mohit Tekriwal, and David Bindel, 30th IEEE International Symposium on Computer Arithmetic , September 2023.
- Towards verified rounding error analysis for stationary iterative methods , by Ariel Kellison, Mohit Tekriwal, Jean-Baptiste Jeannin, and Geoffrey Hulette, in Correctness 2022: Sixth International Workshop on Software Correctness for HPC Applications , November 2022.
- Verified Numerical Methods for Ordinary Differential Equations , by Ariel E. Kellison and Andrew W. Appel, in NSV’22: 15th International Workshop on Numerical Software Verification , August 2022.
- VCFloat2: Floating-point Error Analysis in Coq , by Andrew W. Appel and Ariel E. Kellison, in CPP 2024: Proceedings of the 13th ACM SIGPLAN International Conference on Certified Programs and Proofs , pages 14–29, January 2024.
- C-language floating-point proofs layered with VST and Flocq , by Andrew W. Appel and Yves Bertot, Journal of Formalized Reasoning volume 13, number 1, pages 1-16.
VeriNum’s various projects are supported in part by
- National Science Foundation grant 2219757 “Formally Verified Numerical Methods”, to Princeton University (Appel, Principal Investigator) and grant 2219758 to Cornell University (Bindel)
- National Science Foundation grant 2219997 “Foundational Approaches for End-to-end Formal Verification of Computational Physics” to the University of Michigan (Jeannin and Duraisamy)
- U.S. Department of Energy Computational Science Graduate Fellowship (Ariel Kellison)
- Sandia National Laboratories, funding the collaboration of Sandia participants with these projects
Computational Science & Numerical Analysis
Computational science is a key area related to physical mathematics. The problems of interest in physical mathematics often require computations for their resolution. Conversely, the development of efficient computational algorithms often requires an understanding of the basic properties of the solutions to the equations to be solved numerically. For example, the development of methods for the solution of hyperbolic equations (e.g. shock capturing methods in, say, gas-dynamics) has been characterized by a very close interaction between theoretical, computational, experimental scientists, and engineers.
Department Members in This Field
- Laurent Demanet Applied analysis, Scientific Computing
- Alan Edelman Parallel Computing, Numerical Linear Algebra, Random Matrices
- Steven Johnson Waves, PDEs, Scientific Computing
- Pablo Parrilo Optimization, Control Theory, Computational Algebraic Geometry, Applied Mathematics
- Gilbert Strang Numerical Analysis, Partial Differential Equations
- John Urschel Matrix Analysis, Numerical Linear Algebra, Spectral Graph Theory
Instructors & Postdocs
- Pengning Chao Scientific computing, Nanophotonics, Inverse problems, Fundamental limits
- Ziang Chen applied analysis, applied probability, statistics, optimization, machine learning
Researchers & Visitors
- Keaton Burns PDEs, Spectral Methods, Fluid Dynamics
- Raphaël Pestourie Surrogate Models, AI, Electromagnetic Design, End-to-end Optimization, Inverse Design
Graduate Students*
- Rodrigo Arrieta Candia Numerical methods for PDEs, Numerical Analysis, Scientific Computing, Computational Electromagnetism
- Mo Chen Optimization, Scientific Computing
- Max Daniels High-dimensional statistics, optimization, sampling algorithms, machine learning
- Sarah Greer Imaging, inverse problems, signal processing
- Songchen Tan computational science, numerical analysis, differentiable programming
*Only a partial list of graduate students
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- What Is Quantitative Research? | Definition, Uses & Methods
What Is Quantitative Research? | Definition, Uses & Methods
Published on June 12, 2020 by Pritha Bhandari . Revised on June 22, 2023.
Quantitative research is the process of collecting and analyzing numerical data. It can be used to find patterns and averages, make predictions, test causal relationships, and generalize results to wider populations.
Quantitative research is the opposite of qualitative research , which involves collecting and analyzing non-numerical data (e.g., text, video, or audio).
Quantitative research is widely used in the natural and social sciences: biology, chemistry, psychology, economics, sociology, marketing, etc.
- What is the demographic makeup of Singapore in 2020?
- How has the average temperature changed globally over the last century?
- Does environmental pollution affect the prevalence of honey bees?
- Does working from home increase productivity for people with long commutes?
Table of contents
Quantitative research methods, quantitative data analysis, advantages of quantitative research, disadvantages of quantitative research, other interesting articles, frequently asked questions about quantitative research.
You can use quantitative research methods for descriptive, correlational or experimental research.
- In descriptive research , you simply seek an overall summary of your study variables.
- In correlational research , you investigate relationships between your study variables.
- In experimental research , you systematically examine whether there is a cause-and-effect relationship between variables.
Correlational and experimental research can both be used to formally test hypotheses , or predictions, using statistics. The results may be generalized to broader populations based on the sampling method used.
To collect quantitative data, you will often need to use operational definitions that translate abstract concepts (e.g., mood) into observable and quantifiable measures (e.g., self-ratings of feelings and energy levels).
| Research method | How to use | Example |
|---|---|---|
| Control or manipulate an to measure its effect on a dependent variable. | To test whether an intervention can reduce procrastination in college students, you give equal-sized groups either a procrastination intervention or a comparable task. You compare self-ratings of procrastination behaviors between the groups after the intervention. | |
| Ask questions of a group of people in-person, over-the-phone or online. | You distribute with rating scales to first-year international college students to investigate their experiences of culture shock. | |
| (Systematic) observation | Identify a behavior or occurrence of interest and monitor it in its natural setting. | To study college classroom participation, you sit in on classes to observe them, counting and recording the prevalence of active and passive behaviors by students from different backgrounds. |
| Secondary research | Collect data that has been gathered for other purposes e.g., national surveys or historical records. | To assess whether attitudes towards climate change have changed since the 1980s, you collect relevant questionnaire data from widely available . |
Note that quantitative research is at risk for certain research biases , including information bias , omitted variable bias , sampling bias , or selection bias . Be sure that you’re aware of potential biases as you collect and analyze your data to prevent them from impacting your work too much.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
Once data is collected, you may need to process it before it can be analyzed. For example, survey and test data may need to be transformed from words to numbers. Then, you can use statistical analysis to answer your research questions .
Descriptive statistics will give you a summary of your data and include measures of averages and variability. You can also use graphs, scatter plots and frequency tables to visualize your data and check for any trends or outliers.
Using inferential statistics , you can make predictions or generalizations based on your data. You can test your hypothesis or use your sample data to estimate the population parameter .
First, you use descriptive statistics to get a summary of the data. You find the mean (average) and the mode (most frequent rating) of procrastination of the two groups, and plot the data to see if there are any outliers.
You can also assess the reliability and validity of your data collection methods to indicate how consistently and accurately your methods actually measured what you wanted them to.
Quantitative research is often used to standardize data collection and generalize findings . Strengths of this approach include:
- Replication
Repeating the study is possible because of standardized data collection protocols and tangible definitions of abstract concepts.
- Direct comparisons of results
The study can be reproduced in other cultural settings, times or with different groups of participants. Results can be compared statistically.
- Large samples
Data from large samples can be processed and analyzed using reliable and consistent procedures through quantitative data analysis.
- Hypothesis testing
Using formalized and established hypothesis testing procedures means that you have to carefully consider and report your research variables, predictions, data collection and testing methods before coming to a conclusion.
Despite the benefits of quantitative research, it is sometimes inadequate in explaining complex research topics. Its limitations include:
- Superficiality
Using precise and restrictive operational definitions may inadequately represent complex concepts. For example, the concept of mood may be represented with just a number in quantitative research, but explained with elaboration in qualitative research.
- Narrow focus
Predetermined variables and measurement procedures can mean that you ignore other relevant observations.
- Structural bias
Despite standardized procedures, structural biases can still affect quantitative research. Missing data , imprecise measurements or inappropriate sampling methods are biases that can lead to the wrong conclusions.
- Lack of context
Quantitative research often uses unnatural settings like laboratories or fails to consider historical and cultural contexts that may affect data collection and results.
Prevent plagiarism. Run a free check.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Chi square goodness of fit test
- Degrees of freedom
- Null hypothesis
- Discourse analysis
- Control groups
- Mixed methods research
- Non-probability sampling
- Inclusion and exclusion criteria
Research bias
- Rosenthal effect
- Implicit bias
- Cognitive bias
- Selection bias
- Negativity bias
- Status quo bias
Quantitative research deals with numbers and statistics, while qualitative research deals with words and meanings.
Quantitative methods allow you to systematically measure variables and test hypotheses . Qualitative methods allow you to explore concepts and experiences in more detail.
In mixed methods research , you use both qualitative and quantitative data collection and analysis methods to answer your research question .
Data collection is the systematic process by which observations or measurements are gathered in research. It is used in many different contexts by academics, governments, businesses, and other organizations.
Operationalization means turning abstract conceptual ideas into measurable observations.
For example, the concept of social anxiety isn’t directly observable, but it can be operationally defined in terms of self-rating scores, behavioral avoidance of crowded places, or physical anxiety symptoms in social situations.
Before collecting data , it’s important to consider how you will operationalize the variables that you want to measure.
Reliability and validity are both about how well a method measures something:
- Reliability refers to the consistency of a measure (whether the results can be reproduced under the same conditions).
- Validity refers to the accuracy of a measure (whether the results really do represent what they are supposed to measure).
If you are doing experimental research, you also have to consider the internal and external validity of your experiment.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 22). What Is Quantitative Research? | Definition, Uses & Methods. Scribbr. Retrieved August 21, 2024, from https://www.scribbr.com/methodology/quantitative-research/
Is this article helpful?

Pritha Bhandari
Other students also liked, descriptive statistics | definitions, types, examples, inferential statistics | an easy introduction & examples, "i thought ai proofreading was useless but..".
I've been using Scribbr for years now and I know it's a service that won't disappoint. It does a good job spotting mistakes”
- USC Libraries
- Research Guides
Organizing Your Social Sciences Research Paper
- Quantitative Methods
- Purpose of Guide
- Design Flaws to Avoid
- Independent and Dependent Variables
- Glossary of Research Terms
- Reading Research Effectively
- Narrowing a Topic Idea
- Broadening a Topic Idea
- Extending the Timeliness of a Topic Idea
- Academic Writing Style
- Applying Critical Thinking
- Choosing a Title
- Making an Outline
- Paragraph Development
- Research Process Video Series
- Executive Summary
- The C.A.R.S. Model
- Background Information
- The Research Problem/Question
- Theoretical Framework
- Citation Tracking
- Content Alert Services
- Evaluating Sources
- Primary Sources
- Secondary Sources
- Tiertiary Sources
- Scholarly vs. Popular Publications
- Qualitative Methods
- Insiderness
- Using Non-Textual Elements
- Limitations of the Study
- Common Grammar Mistakes
- Writing Concisely
- Avoiding Plagiarism
- Footnotes or Endnotes?
- Further Readings
- Generative AI and Writing
- USC Libraries Tutorials and Other Guides
- Bibliography
Quantitative methods emphasize objective measurements and the statistical, mathematical, or numerical analysis of data collected through polls, questionnaires, and surveys, or by manipulating pre-existing statistical data using computational techniques . Quantitative research focuses on gathering numerical data and generalizing it across groups of people or to explain a particular phenomenon.
Babbie, Earl R. The Practice of Social Research . 12th ed. Belmont, CA: Wadsworth Cengage, 2010; Muijs, Daniel. Doing Quantitative Research in Education with SPSS . 2nd edition. London: SAGE Publications, 2010.
Need Help Locating Statistics?
Resources for locating data and statistics can be found here:
Statistics & Data Research Guide
Characteristics of Quantitative Research
Your goal in conducting quantitative research study is to determine the relationship between one thing [an independent variable] and another [a dependent or outcome variable] within a population. Quantitative research designs are either descriptive [subjects usually measured once] or experimental [subjects measured before and after a treatment]. A descriptive study establishes only associations between variables; an experimental study establishes causality.
Quantitative research deals in numbers, logic, and an objective stance. Quantitative research focuses on numeric and unchanging data and detailed, convergent reasoning rather than divergent reasoning [i.e., the generation of a variety of ideas about a research problem in a spontaneous, free-flowing manner].
Its main characteristics are :
- The data is usually gathered using structured research instruments.
- The results are based on larger sample sizes that are representative of the population.
- The research study can usually be replicated or repeated, given its high reliability.
- Researcher has a clearly defined research question to which objective answers are sought.
- All aspects of the study are carefully designed before data is collected.
- Data are in the form of numbers and statistics, often arranged in tables, charts, figures, or other non-textual forms.
- Project can be used to generalize concepts more widely, predict future results, or investigate causal relationships.
- Researcher uses tools, such as questionnaires or computer software, to collect numerical data.
The overarching aim of a quantitative research study is to classify features, count them, and construct statistical models in an attempt to explain what is observed.
Things to keep in mind when reporting the results of a study using quantitative methods :
- Explain the data collected and their statistical treatment as well as all relevant results in relation to the research problem you are investigating. Interpretation of results is not appropriate in this section.
- Report unanticipated events that occurred during your data collection. Explain how the actual analysis differs from the planned analysis. Explain your handling of missing data and why any missing data does not undermine the validity of your analysis.
- Explain the techniques you used to "clean" your data set.
- Choose a minimally sufficient statistical procedure ; provide a rationale for its use and a reference for it. Specify any computer programs used.
- Describe the assumptions for each procedure and the steps you took to ensure that they were not violated.
- When using inferential statistics , provide the descriptive statistics, confidence intervals, and sample sizes for each variable as well as the value of the test statistic, its direction, the degrees of freedom, and the significance level [report the actual p value].
- Avoid inferring causality , particularly in nonrandomized designs or without further experimentation.
- Use tables to provide exact values ; use figures to convey global effects. Keep figures small in size; include graphic representations of confidence intervals whenever possible.
- Always tell the reader what to look for in tables and figures .
NOTE: When using pre-existing statistical data gathered and made available by anyone other than yourself [e.g., government agency], you still must report on the methods that were used to gather the data and describe any missing data that exists and, if there is any, provide a clear explanation why the missing data does not undermine the validity of your final analysis.
Babbie, Earl R. The Practice of Social Research . 12th ed. Belmont, CA: Wadsworth Cengage, 2010; Brians, Craig Leonard et al. Empirical Political Analysis: Quantitative and Qualitative Research Methods . 8th ed. Boston, MA: Longman, 2011; McNabb, David E. Research Methods in Public Administration and Nonprofit Management: Quantitative and Qualitative Approaches . 2nd ed. Armonk, NY: M.E. Sharpe, 2008; Quantitative Research Methods. Writing@CSU. Colorado State University; Singh, Kultar. Quantitative Social Research Methods . Los Angeles, CA: Sage, 2007.
Basic Research Design for Quantitative Studies
Before designing a quantitative research study, you must decide whether it will be descriptive or experimental because this will dictate how you gather, analyze, and interpret the results. A descriptive study is governed by the following rules: subjects are generally measured once; the intention is to only establish associations between variables; and, the study may include a sample population of hundreds or thousands of subjects to ensure that a valid estimate of a generalized relationship between variables has been obtained. An experimental design includes subjects measured before and after a particular treatment, the sample population may be very small and purposefully chosen, and it is intended to establish causality between variables. Introduction The introduction to a quantitative study is usually written in the present tense and from the third person point of view. It covers the following information:
- Identifies the research problem -- as with any academic study, you must state clearly and concisely the research problem being investigated.
- Reviews the literature -- review scholarship on the topic, synthesizing key themes and, if necessary, noting studies that have used similar methods of inquiry and analysis. Note where key gaps exist and how your study helps to fill these gaps or clarifies existing knowledge.
- Describes the theoretical framework -- provide an outline of the theory or hypothesis underpinning your study. If necessary, define unfamiliar or complex terms, concepts, or ideas and provide the appropriate background information to place the research problem in proper context [e.g., historical, cultural, economic, etc.].
Methodology The methods section of a quantitative study should describe how each objective of your study will be achieved. Be sure to provide enough detail to enable the reader can make an informed assessment of the methods being used to obtain results associated with the research problem. The methods section should be presented in the past tense.
- Study population and sampling -- where did the data come from; how robust is it; note where gaps exist or what was excluded. Note the procedures used for their selection;
- Data collection – describe the tools and methods used to collect information and identify the variables being measured; describe the methods used to obtain the data; and, note if the data was pre-existing [i.e., government data] or you gathered it yourself. If you gathered it yourself, describe what type of instrument you used and why. Note that no data set is perfect--describe any limitations in methods of gathering data.
- Data analysis -- describe the procedures for processing and analyzing the data. If appropriate, describe the specific instruments of analysis used to study each research objective, including mathematical techniques and the type of computer software used to manipulate the data.
Results The finding of your study should be written objectively and in a succinct and precise format. In quantitative studies, it is common to use graphs, tables, charts, and other non-textual elements to help the reader understand the data. Make sure that non-textual elements do not stand in isolation from the text but are being used to supplement the overall description of the results and to help clarify key points being made. Further information about how to effectively present data using charts and graphs can be found here .
- Statistical analysis -- how did you analyze the data? What were the key findings from the data? The findings should be present in a logical, sequential order. Describe but do not interpret these trends or negative results; save that for the discussion section. The results should be presented in the past tense.
Discussion Discussions should be analytic, logical, and comprehensive. The discussion should meld together your findings in relation to those identified in the literature review, and placed within the context of the theoretical framework underpinning the study. The discussion should be presented in the present tense.
- Interpretation of results -- reiterate the research problem being investigated and compare and contrast the findings with the research questions underlying the study. Did they affirm predicted outcomes or did the data refute it?
- Description of trends, comparison of groups, or relationships among variables -- describe any trends that emerged from your analysis and explain all unanticipated and statistical insignificant findings.
- Discussion of implications – what is the meaning of your results? Highlight key findings based on the overall results and note findings that you believe are important. How have the results helped fill gaps in understanding the research problem?
- Limitations -- describe any limitations or unavoidable bias in your study and, if necessary, note why these limitations did not inhibit effective interpretation of the results.
Conclusion End your study by to summarizing the topic and provide a final comment and assessment of the study.
- Summary of findings – synthesize the answers to your research questions. Do not report any statistical data here; just provide a narrative summary of the key findings and describe what was learned that you did not know before conducting the study.
- Recommendations – if appropriate to the aim of the assignment, tie key findings with policy recommendations or actions to be taken in practice.
- Future research – note the need for future research linked to your study’s limitations or to any remaining gaps in the literature that were not addressed in your study.
Black, Thomas R. Doing Quantitative Research in the Social Sciences: An Integrated Approach to Research Design, Measurement and Statistics . London: Sage, 1999; Gay,L. R. and Peter Airasain. Educational Research: Competencies for Analysis and Applications . 7th edition. Upper Saddle River, NJ: Merril Prentice Hall, 2003; Hector, Anestine. An Overview of Quantitative Research in Composition and TESOL . Department of English, Indiana University of Pennsylvania; Hopkins, Will G. “Quantitative Research Design.” Sportscience 4, 1 (2000); "A Strategy for Writing Up Research Results. The Structure, Format, Content, and Style of a Journal-Style Scientific Paper." Department of Biology. Bates College; Nenty, H. Johnson. "Writing a Quantitative Research Thesis." International Journal of Educational Science 1 (2009): 19-32; Ouyang, Ronghua (John). Basic Inquiry of Quantitative Research . Kennesaw State University.
Strengths of Using Quantitative Methods
Quantitative researchers try to recognize and isolate specific variables contained within the study framework, seek correlation, relationships and causality, and attempt to control the environment in which the data is collected to avoid the risk of variables, other than the one being studied, accounting for the relationships identified.
Among the specific strengths of using quantitative methods to study social science research problems:
- Allows for a broader study, involving a greater number of subjects, and enhancing the generalization of the results;
- Allows for greater objectivity and accuracy of results. Generally, quantitative methods are designed to provide summaries of data that support generalizations about the phenomenon under study. In order to accomplish this, quantitative research usually involves few variables and many cases, and employs prescribed procedures to ensure validity and reliability;
- Applying well established standards means that the research can be replicated, and then analyzed and compared with similar studies;
- You can summarize vast sources of information and make comparisons across categories and over time; and,
- Personal bias can be avoided by keeping a 'distance' from participating subjects and using accepted computational techniques .
Babbie, Earl R. The Practice of Social Research . 12th ed. Belmont, CA: Wadsworth Cengage, 2010; Brians, Craig Leonard et al. Empirical Political Analysis: Quantitative and Qualitative Research Methods . 8th ed. Boston, MA: Longman, 2011; McNabb, David E. Research Methods in Public Administration and Nonprofit Management: Quantitative and Qualitative Approaches . 2nd ed. Armonk, NY: M.E. Sharpe, 2008; Singh, Kultar. Quantitative Social Research Methods . Los Angeles, CA: Sage, 2007.
Limitations of Using Quantitative Methods
Quantitative methods presume to have an objective approach to studying research problems, where data is controlled and measured, to address the accumulation of facts, and to determine the causes of behavior. As a consequence, the results of quantitative research may be statistically significant but are often humanly insignificant.
Some specific limitations associated with using quantitative methods to study research problems in the social sciences include:
- Quantitative data is more efficient and able to test hypotheses, but may miss contextual detail;
- Uses a static and rigid approach and so employs an inflexible process of discovery;
- The development of standard questions by researchers can lead to "structural bias" and false representation, where the data actually reflects the view of the researcher instead of the participating subject;
- Results provide less detail on behavior, attitudes, and motivation;
- Researcher may collect a much narrower and sometimes superficial dataset;
- Results are limited as they provide numerical descriptions rather than detailed narrative and generally provide less elaborate accounts of human perception;
- The research is often carried out in an unnatural, artificial environment so that a level of control can be applied to the exercise. This level of control might not normally be in place in the real world thus yielding "laboratory results" as opposed to "real world results"; and,
- Preset answers will not necessarily reflect how people really feel about a subject and, in some cases, might just be the closest match to the preconceived hypothesis.
Research Tip
Finding Examples of How to Apply Different Types of Research Methods
SAGE publications is a major publisher of studies about how to design and conduct research in the social and behavioral sciences. Their SAGE Research Methods Online and Cases database includes contents from books, articles, encyclopedias, handbooks, and videos covering social science research design and methods including the complete Little Green Book Series of Quantitative Applications in the Social Sciences and the Little Blue Book Series of Qualitative Research techniques. The database also includes case studies outlining the research methods used in real research projects. This is an excellent source for finding definitions of key terms and descriptions of research design and practice, techniques of data gathering, analysis, and reporting, and information about theories of research [e.g., grounded theory]. The database covers both qualitative and quantitative research methods as well as mixed methods approaches to conducting research.
SAGE Research Methods Online and Cases
- << Previous: Qualitative Methods
- Next: Insiderness >>
- Last Updated: Aug 21, 2024 8:54 AM
- URL: https://libguides.usc.edu/writingguide
Qualitative Analysis of a Novel Numerical Method for Solving Non-linear Ordinary Differential Equations
- Original Paper
- Published: 17 April 2024
- Volume 10 , article number 99 , ( 2024 )
Cite this article

- Sonali Kaushik 1 &
- Rajesh Kumar 2
163 Accesses
Explore all metrics
The dynamics of innumerable real-world phenomena is represented with the help of non-linear ordinary differential equations (NODEs). There is a growing trend of solving these equations using accurate and easy to implement methods. The goal of this research work is to create a numerical method to solve the first-order NODEs (FNODEs) by coupling of the well-known trapezoidal method with a newly developed semi-analytical technique called the Laplace optimized decomposition method (LODM). The novelty of this coupling lies in the improvement of order of accuracy of the scheme when the terms in the series solution are increased. The article discusses the qualitative behavior of the new method, i.e., consistency, stability and convergence. Several numerical test cases of the non-linear differential equations are considered to validate our findings.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions

Similar content being viewed by others
Analysis of some dynamical systems by combination of two different methods

Novel approach for solving higher-order differential equations with applications to the Van der Pol and Van der Pol–Duffing equations

Nonlinear Initial Value Ordinary Differential Equations
Data availability.
Enquiries about data availability should be directed to the authors.
Simmons, G.F.: Differential Equations with Applications and Historical Notes. CRC Press, Boca Raton (2016)
Google Scholar
Nagle, R.K., Saff, E.B., Snider, A.D.: Fundamentals of Differential Equations. Pearson, London (2017)
Nadeem, M., He, J.-H., He, C.-H., Sedighi, H.M., Shirazi, A.: A numerical solution of nonlinear fractional Newell-Whitehead-Segel equation using natural transform. TWMS J. Pure Appl. Math. 13 (2), 168–182 (2022)
Liu, J., Nadeem, M., Habib, M., Karim, S., Or Roshid, H.: Numerical investigation of the nonlinear coupled fractional massive thirring equation using two-scale approach, Complexity 2022 (2022)
Nadeem, M., He, J.-H., Islam, A.: The homotopy perturbation method for fractional differential equations: part 1 mohand transform. Int. J. Numer. Methods Heat Fluid Flow 31 (11), 3490–3504 (2021)
Article Google Scholar
Tran, T.V.H., Pavelková, D., Homolka, L.: Solow model with technological progress: an empirical study of economic growth in Vietnam through Ardl approach. Quality-Access to Success 23 (186) (2022)
Briec, W., Lasselle, L.: On some relations between a continuous time Luenberger productivity indicator and the Solow model. Bull. Econ. Res. 74 (2), 484–502 (2022)
Article MathSciNet Google Scholar
Danca, M., Codreanu, S., Bako, B.: Detailed analysis of a nonlinear prey–predator model. J. Biol. Phys. 23 (1), 11 (1997)
Bentout, S., Djilali, S., Atangana, A.: Bifurcation analysis of an age-structured prey–predator model with infection developed in prey. Math. Methods Appl. Sci. 45 (3), 1189–1208 (2022)
Campos, L.: Non-Linear Differential Equations and Dynamical Systems: Ordinary Differential Equations with Applications to Trajectories and Oscillations. CRC Press, Boca Raton (2019)
Book Google Scholar
Shah, N.A., Ahmad, I., Bazighifan, O., Abouelregal, A.E., Ahmad, H.: Multistage optimal homotopy asymptotic method for the nonlinear Riccati ordinary differential equation in nonlinear physics. Appl. Math. 14 (6), 1009–1016 (2020)
MathSciNet Google Scholar
LeVeque, R.J.: Finite Difference Methods for Ordinary and Partial Differential Equations. Steady-state and Time-Dependent Problems. SIAM, Philadelphia (2007)
Mickens, R.E.: Nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 8 (9), 823–847 (2002)
Mehdizadeh Khalsaraei, M., Khodadosti, F.: Nonstandard finite difference schemes for differential equations. Sahand Commun. Math. Anal. 1 (2), 47–54 (2014)
Thirumalai, S., Seshadri, R., Yuzbasi, S.: Spectral solutions of fractional differential equations modelling combined drug therapy for HIV infection. Chaos, Solitons & Fractals 151 , 111234 (2021)
Evans, G.A., Blackledge, J.M., Yardley, P.D.: Finite element method for ordinary differential equations. In: Numerical Methods for Partial Differential Equations, pp. 123–164. Springer(2000)
Deng, K., Xiong, Z.: Superconvergence of a discontinuous finite element method for a nonlinear ordinary differential equation. Appl. Math. Comput. 217 (7), 3511–3515 (2010)
Wriggers, P.: Nonlinear Finite Element Methods. Springer, Berlin (2008)
Gonsalves, S., Swapna, G.: Finite element study of nanofluid through porous nonlinear stretching surface under convective boundary conditions. Mater. Today Proc. (2023)
Al-Omari, A., Schüttler, H.-B., Arnold, J., Taha, T.: Solving nonlinear systems of first order ordinary differential equations using a Galerkin finite element method. IEEE Access 1 , 408–417 (2013)
Odibat, Z.: An optimized decomposition method for nonlinear ordinary and partial differential equations. Phys. A 541 , 123323 (2020)
Jafari, H., Daftardar-Gejji, V.: Revised adomian decomposition method for solving systems of ordinary and fractional differential equations. Appl. Math. Comput. 181 (1), 598–608 (2006)
Liao, S.: Homotopy Analysis Method in Nonlinear Differential Equations. Springer, Berlin (2012)
Odibat, Z.: An improved optimal homotopy analysis algorithm for nonlinear differential equations. J. Math. Anal. Appl. 488 (2), 124089 (2020)
He, J.-H., Latifizadeh, H.: A general numerical algorithm for nonlinear differential equations by the variational iteration method. Int. J. Numer. Methods Heat Fluid Flow 30 (11), 4797–4810 (2020)
Biazar, J., Ghazvini, H.: He’s variational iteration method for solving linear and non-linear systems of ordinary differential equations. Appl. Math. Comput. 191 (1), 287–297 (2007)
Ramos, J.I.: On the variational iteration method and other iterative techniques for nonlinear differential equations. Appl. Math. Comput. 199 (1), 39–69 (2008)
Geng, F.: A modified variational iteration method for solving Riccati differential equations. Comput. Math. Appl. 60 (7), 1868–1872 (2010)
Kumar, R.V., Sarris, I.E., Sowmya, G., Abdulrahman, A.: Iterative solutions for the nonlinear heat transfer equation of a convective-radiative annular fin with power law temperature-dependent thermal properties. Symmetry 15 (6), 1204 (2023)
Sowmya, G., Kumar, R.S.V., Banu, Y.: Thermal performance of a longitudinal fin under the influence of magnetic field using sumudu transform method with pade approximant (stm-pa). ZAMM J. Appl. Math. Mech. 103 , e202100526 (2023)
Varun Kumar, R.S., Sowmya, G., Jayaprakash, M.C., Prasannakumara, B.C., Khan, M.I., Guedri, K., Kumam, P., Sitthithakerngkiet, K., Galal, A.M.: Assessment of thermal distribution through an inclined radiative–convective porous fin of concave profile using generalized residual power series method (GRPSM). Sci. Rep. (2022). https://doi.org/10.1038/s41598-022-15396-z
Kaushik, S., Kumar, R.: A novel optimized decomposition method for Smoluchowski’s aggregation equation. J. Comput. Appl. Math. 419 , 114710 (2023)
Odibat, Z.: The optimized decomposition method for a reliable treatment of ivps for second order differential equations. Phys. Scr. 96 (9), 095206 (2021)
Beghami, W., Maayah, B., Bushnaq, S., Abu Arqub, O.: The laplace optimized decomposition method for solving systems of partial differential equations of fractional order. Int. J. Appl. Comput. Math. 8 , 52 (2022). https://doi.org/10.1007/s40819-022-01256-x
Kaushik, S., Hussain, S., Kumar, R.: Laplace transform-based approximation methods for solving pure aggregation and breakage equations. Math. Methods Appl. Sci. 46 (16), 17402–17421 (2023)
Patade, J., Bhalekar, S.: A new numerical method based on Daftardar-Gejji and Jafari technique for solving differential equations. World J. Model. Simul. 11 , 256–271 (2015)
Patade, J., Bhalekar, S.: A novel numerical method for solving Volterra integro-differential equations. Int. J. Appl. Comput. Math. 6 (1), 1–19 (2020)
Ali, L., Islam, S., Gul, T., Amiri, I.S.: Solution of nonlinear problems by a new analytical technique using Daftardar-Gejji and Jafari polynomials. Adv. Mech. Eng. 11 (12), 1687814019896962 (2019)
Download references
Rajesh Kumar wishes to thank Science and Engineering Research Board (SERB), Department of Science and Technology (DST), India, for the funding through the project MTR/2021/000866.
Author information
Authors and affiliations.
Department of Mathematics, School of Advanced Sciences, VIT-AP University, Amaravati, 522237, India
Sonali Kaushik
Department of Mathematics, BITS Pilani, Pilani Campus, Pilani, Rajasthan, 333031, India
Rajesh Kumar
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Sonali Kaushik .
Ethics declarations
Competing interests.
The authors have not disclosed any competing interests.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reprints and permissions
About this article
Kaushik, S., Kumar, R. Qualitative Analysis of a Novel Numerical Method for Solving Non-linear Ordinary Differential Equations. Int. J. Appl. Comput. Math 10 , 99 (2024). https://doi.org/10.1007/s40819-024-01735-3
Download citation
Accepted : 27 March 2024
Published : 17 April 2024
DOI : https://doi.org/10.1007/s40819-024-01735-3
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- First-order non-linear differential equations
- Trapezoidal method
- Semi-analytical method
- Laplace transform
- Laplace optimized decomposition method
- Consistency
- Convergence
Mathematics Subject Classification
- Primary 45K05
- Secondary 34A34
- Find a journal
- Publish with us
- Track your research
- Privacy Policy

Home » Quantitative Research – Methods, Types and Analysis
Quantitative Research – Methods, Types and Analysis
Table of Contents

Quantitative Research
Quantitative research is a type of research that collects and analyzes numerical data to test hypotheses and answer research questions . This research typically involves a large sample size and uses statistical analysis to make inferences about a population based on the data collected. It often involves the use of surveys, experiments, or other structured data collection methods to gather quantitative data.
Quantitative Research Methods

Quantitative Research Methods are as follows:
Descriptive Research Design
Descriptive research design is used to describe the characteristics of a population or phenomenon being studied. This research method is used to answer the questions of what, where, when, and how. Descriptive research designs use a variety of methods such as observation, case studies, and surveys to collect data. The data is then analyzed using statistical tools to identify patterns and relationships.
Correlational Research Design
Correlational research design is used to investigate the relationship between two or more variables. Researchers use correlational research to determine whether a relationship exists between variables and to what extent they are related. This research method involves collecting data from a sample and analyzing it using statistical tools such as correlation coefficients.
Quasi-experimental Research Design
Quasi-experimental research design is used to investigate cause-and-effect relationships between variables. This research method is similar to experimental research design, but it lacks full control over the independent variable. Researchers use quasi-experimental research designs when it is not feasible or ethical to manipulate the independent variable.
Experimental Research Design
Experimental research design is used to investigate cause-and-effect relationships between variables. This research method involves manipulating the independent variable and observing the effects on the dependent variable. Researchers use experimental research designs to test hypotheses and establish cause-and-effect relationships.
Survey Research
Survey research involves collecting data from a sample of individuals using a standardized questionnaire. This research method is used to gather information on attitudes, beliefs, and behaviors of individuals. Researchers use survey research to collect data quickly and efficiently from a large sample size. Survey research can be conducted through various methods such as online, phone, mail, or in-person interviews.
Quantitative Research Analysis Methods
Here are some commonly used quantitative research analysis methods:
Statistical Analysis
Statistical analysis is the most common quantitative research analysis method. It involves using statistical tools and techniques to analyze the numerical data collected during the research process. Statistical analysis can be used to identify patterns, trends, and relationships between variables, and to test hypotheses and theories.
Regression Analysis
Regression analysis is a statistical technique used to analyze the relationship between one dependent variable and one or more independent variables. Researchers use regression analysis to identify and quantify the impact of independent variables on the dependent variable.
Factor Analysis
Factor analysis is a statistical technique used to identify underlying factors that explain the correlations among a set of variables. Researchers use factor analysis to reduce a large number of variables to a smaller set of factors that capture the most important information.
Structural Equation Modeling
Structural equation modeling is a statistical technique used to test complex relationships between variables. It involves specifying a model that includes both observed and unobserved variables, and then using statistical methods to test the fit of the model to the data.
Time Series Analysis
Time series analysis is a statistical technique used to analyze data that is collected over time. It involves identifying patterns and trends in the data, as well as any seasonal or cyclical variations.
Multilevel Modeling
Multilevel modeling is a statistical technique used to analyze data that is nested within multiple levels. For example, researchers might use multilevel modeling to analyze data that is collected from individuals who are nested within groups, such as students nested within schools.
Applications of Quantitative Research
Quantitative research has many applications across a wide range of fields. Here are some common examples:
- Market Research : Quantitative research is used extensively in market research to understand consumer behavior, preferences, and trends. Researchers use surveys, experiments, and other quantitative methods to collect data that can inform marketing strategies, product development, and pricing decisions.
- Health Research: Quantitative research is used in health research to study the effectiveness of medical treatments, identify risk factors for diseases, and track health outcomes over time. Researchers use statistical methods to analyze data from clinical trials, surveys, and other sources to inform medical practice and policy.
- Social Science Research: Quantitative research is used in social science research to study human behavior, attitudes, and social structures. Researchers use surveys, experiments, and other quantitative methods to collect data that can inform social policies, educational programs, and community interventions.
- Education Research: Quantitative research is used in education research to study the effectiveness of teaching methods, assess student learning outcomes, and identify factors that influence student success. Researchers use experimental and quasi-experimental designs, as well as surveys and other quantitative methods, to collect and analyze data.
- Environmental Research: Quantitative research is used in environmental research to study the impact of human activities on the environment, assess the effectiveness of conservation strategies, and identify ways to reduce environmental risks. Researchers use statistical methods to analyze data from field studies, experiments, and other sources.
Characteristics of Quantitative Research
Here are some key characteristics of quantitative research:
- Numerical data : Quantitative research involves collecting numerical data through standardized methods such as surveys, experiments, and observational studies. This data is analyzed using statistical methods to identify patterns and relationships.
- Large sample size: Quantitative research often involves collecting data from a large sample of individuals or groups in order to increase the reliability and generalizability of the findings.
- Objective approach: Quantitative research aims to be objective and impartial in its approach, focusing on the collection and analysis of data rather than personal beliefs, opinions, or experiences.
- Control over variables: Quantitative research often involves manipulating variables to test hypotheses and establish cause-and-effect relationships. Researchers aim to control for extraneous variables that may impact the results.
- Replicable : Quantitative research aims to be replicable, meaning that other researchers should be able to conduct similar studies and obtain similar results using the same methods.
- Statistical analysis: Quantitative research involves using statistical tools and techniques to analyze the numerical data collected during the research process. Statistical analysis allows researchers to identify patterns, trends, and relationships between variables, and to test hypotheses and theories.
- Generalizability: Quantitative research aims to produce findings that can be generalized to larger populations beyond the specific sample studied. This is achieved through the use of random sampling methods and statistical inference.
Examples of Quantitative Research
Here are some examples of quantitative research in different fields:
- Market Research: A company conducts a survey of 1000 consumers to determine their brand awareness and preferences. The data is analyzed using statistical methods to identify trends and patterns that can inform marketing strategies.
- Health Research : A researcher conducts a randomized controlled trial to test the effectiveness of a new drug for treating a particular medical condition. The study involves collecting data from a large sample of patients and analyzing the results using statistical methods.
- Social Science Research : A sociologist conducts a survey of 500 people to study attitudes toward immigration in a particular country. The data is analyzed using statistical methods to identify factors that influence these attitudes.
- Education Research: A researcher conducts an experiment to compare the effectiveness of two different teaching methods for improving student learning outcomes. The study involves randomly assigning students to different groups and collecting data on their performance on standardized tests.
- Environmental Research : A team of researchers conduct a study to investigate the impact of climate change on the distribution and abundance of a particular species of plant or animal. The study involves collecting data on environmental factors and population sizes over time and analyzing the results using statistical methods.
- Psychology : A researcher conducts a survey of 500 college students to investigate the relationship between social media use and mental health. The data is analyzed using statistical methods to identify correlations and potential causal relationships.
- Political Science: A team of researchers conducts a study to investigate voter behavior during an election. They use survey methods to collect data on voting patterns, demographics, and political attitudes, and analyze the results using statistical methods.
How to Conduct Quantitative Research
Here is a general overview of how to conduct quantitative research:
- Develop a research question: The first step in conducting quantitative research is to develop a clear and specific research question. This question should be based on a gap in existing knowledge, and should be answerable using quantitative methods.
- Develop a research design: Once you have a research question, you will need to develop a research design. This involves deciding on the appropriate methods to collect data, such as surveys, experiments, or observational studies. You will also need to determine the appropriate sample size, data collection instruments, and data analysis techniques.
- Collect data: The next step is to collect data. This may involve administering surveys or questionnaires, conducting experiments, or gathering data from existing sources. It is important to use standardized methods to ensure that the data is reliable and valid.
- Analyze data : Once the data has been collected, it is time to analyze it. This involves using statistical methods to identify patterns, trends, and relationships between variables. Common statistical techniques include correlation analysis, regression analysis, and hypothesis testing.
- Interpret results: After analyzing the data, you will need to interpret the results. This involves identifying the key findings, determining their significance, and drawing conclusions based on the data.
- Communicate findings: Finally, you will need to communicate your findings. This may involve writing a research report, presenting at a conference, or publishing in a peer-reviewed journal. It is important to clearly communicate the research question, methods, results, and conclusions to ensure that others can understand and replicate your research.
When to use Quantitative Research
Here are some situations when quantitative research can be appropriate:
- To test a hypothesis: Quantitative research is often used to test a hypothesis or a theory. It involves collecting numerical data and using statistical analysis to determine if the data supports or refutes the hypothesis.
- To generalize findings: If you want to generalize the findings of your study to a larger population, quantitative research can be useful. This is because it allows you to collect numerical data from a representative sample of the population and use statistical analysis to make inferences about the population as a whole.
- To measure relationships between variables: If you want to measure the relationship between two or more variables, such as the relationship between age and income, or between education level and job satisfaction, quantitative research can be useful. It allows you to collect numerical data on both variables and use statistical analysis to determine the strength and direction of the relationship.
- To identify patterns or trends: Quantitative research can be useful for identifying patterns or trends in data. For example, you can use quantitative research to identify trends in consumer behavior or to identify patterns in stock market data.
- To quantify attitudes or opinions : If you want to measure attitudes or opinions on a particular topic, quantitative research can be useful. It allows you to collect numerical data using surveys or questionnaires and analyze the data using statistical methods to determine the prevalence of certain attitudes or opinions.
Purpose of Quantitative Research
The purpose of quantitative research is to systematically investigate and measure the relationships between variables or phenomena using numerical data and statistical analysis. The main objectives of quantitative research include:
- Description : To provide a detailed and accurate description of a particular phenomenon or population.
- Explanation : To explain the reasons for the occurrence of a particular phenomenon, such as identifying the factors that influence a behavior or attitude.
- Prediction : To predict future trends or behaviors based on past patterns and relationships between variables.
- Control : To identify the best strategies for controlling or influencing a particular outcome or behavior.
Quantitative research is used in many different fields, including social sciences, business, engineering, and health sciences. It can be used to investigate a wide range of phenomena, from human behavior and attitudes to physical and biological processes. The purpose of quantitative research is to provide reliable and valid data that can be used to inform decision-making and improve understanding of the world around us.
Advantages of Quantitative Research
There are several advantages of quantitative research, including:
- Objectivity : Quantitative research is based on objective data and statistical analysis, which reduces the potential for bias or subjectivity in the research process.
- Reproducibility : Because quantitative research involves standardized methods and measurements, it is more likely to be reproducible and reliable.
- Generalizability : Quantitative research allows for generalizations to be made about a population based on a representative sample, which can inform decision-making and policy development.
- Precision : Quantitative research allows for precise measurement and analysis of data, which can provide a more accurate understanding of phenomena and relationships between variables.
- Efficiency : Quantitative research can be conducted relatively quickly and efficiently, especially when compared to qualitative research, which may involve lengthy data collection and analysis.
- Large sample sizes : Quantitative research can accommodate large sample sizes, which can increase the representativeness and generalizability of the results.
Limitations of Quantitative Research
There are several limitations of quantitative research, including:
- Limited understanding of context: Quantitative research typically focuses on numerical data and statistical analysis, which may not provide a comprehensive understanding of the context or underlying factors that influence a phenomenon.
- Simplification of complex phenomena: Quantitative research often involves simplifying complex phenomena into measurable variables, which may not capture the full complexity of the phenomenon being studied.
- Potential for researcher bias: Although quantitative research aims to be objective, there is still the potential for researcher bias in areas such as sampling, data collection, and data analysis.
- Limited ability to explore new ideas: Quantitative research is often based on pre-determined research questions and hypotheses, which may limit the ability to explore new ideas or unexpected findings.
- Limited ability to capture subjective experiences : Quantitative research is typically focused on objective data and may not capture the subjective experiences of individuals or groups being studied.
- Ethical concerns : Quantitative research may raise ethical concerns, such as invasion of privacy or the potential for harm to participants.
About the author
Muhammad Hassan
Researcher, Academic Writer, Web developer
You may also like

Triangulation in Research – Types, Methods and...

Applied Research – Types, Methods and Examples

One-to-One Interview – Methods and Guide

Correlational Research – Methods, Types and...

Qualitative Research – Methods, Analysis Types...

Quasi-Experimental Research Design – Types...
- Academic Calendar
- How Online Learning Works
- Faculty Support
- Apply and Enroll
- Apply for Admission
- Enroll in Courses
- Courses by Semester
- Tuition and Fees
- Military and Veterans
- Academics FAQ
- Programs and Courses
- Graduate Programs
- Certificate Programs
- Professional Development Programs
- Course Catalog
- Courses FAQ
- Student Resources
- Online Course Homepages
- Site Course Homepages
- Exams and Homework
- Technical Support
- Graduate Program Procedures
- Course Drop & Withdrawals
- University Resources
- Students FAQ
CE 536 Introduction to Numerical Methods for Civil Engineers
3 Credit Hours
This is an entry level graduate course intended to give an introduction to widely used numerical methods through application to several civil and environmental engineering problems. The emphasis will be on the breadth of topics and applications; however, to the extent possible, the mathematical theory behind the numerical methods will also be presented. The course is expected to lay foundation for students beginning to engage in research projects that involve numerical methods. Student will use MATLAB as a tool in the course. Experience with MATLAB is not required. The course will be taught in an interactive setting in a computer equipped classroom.
Prerequisite
For graduate students in civil engineering, there are no formal prerequisites or co-requisites. Undergraduate students should have a GPA of 3.0 or better and Junior standing. Discuss with instructor for any clarification regarding these requirements.
Course Objectives
Upon completion of the course, the students will be able to:
- Use MATLAB as a programming language for engineering problem solving.
- Describe and apply basic numerical methods for civil engineering problem solving.
- Develop algorithms and programs for solving civil engineering problems involving: (i) multi-dimensional integration, (ii) multivariate differentiation, (iii) ordinary differential equations, (iv) partial differential equations, (v) optimization, and (vi) curve fitting or inverse problems.
Course Requirements
Typically 7 homework assignments, 1 mini-project report, and a take-home final exam. A weighted average grade will be calculated as follows:
- Assignments – 40%
- Online Quizzes – 10%
- Mini-Project – 15%
- Final exam – 35%
+/- Grading system will be used. MATLAB software is required (see below under computer requirements).
Course Organization
| Module | Topic | Lectures: 75 min |
|---|---|---|
| 1.1 | General MATLAB commands and features | Lectures 1 – 2 |
| 1.2 | Simple Civil Engineering Examples | Lecture 3 |
| 2.1 | Numerical integration techniques and civil engineering applications | Lectures 4 – 6 |
| 2.2 | Numerical differentiation with applications in groundwater flow | Lecture 7 |
| 3.1 | Runge-Kutta methods with applications in structural and environmental engineering | Lectures 8 – 9 |
| 3.2 | Stiff systems with applications in environmental engineering | Lecture 10 |
| 3.3 | Boundary value problems in structural and environmental engineering | Lectures 11 – 12 |
| 4.1 | Introduction to finite difference methods with civil engineering examples | Lectures 13 – 15 |
| 4.2 | Linear and non-linear system solution (direct and iterative methods) | Lecture 16 |
| 4.3 | Applications in groundwater flow and transport | Lecture 17 |
| 4.4 | Matlab PDE toolbox | Lecture 18 |
| 4.5 | Introduction to finite element methods with application to groundwater flow | Lecture 19 |
| 5.1 | Direct methods with applications in environmental and structural engineering | Lecture 20 |
| 5.2 | Gradient based methods with applications in water resources engineering | Lectures 21 – 23 |
| 5.3 | Heuristic methods with applications in structural and water resources engineering | Lectures 24 – 25 |
| 5.4 | Design applications in structural and environmental engineering | Lecture 26 |
| 6.1 | Linear and non-linear regression | Lecture 27 |
| 6.2 | Direct methods | Lecture 28 |
| 6.3 | Indirect methods | Lecture 28 |
| 6.4 | Applications in Civil Engineering | Lecture 29 |
Recommended Textbook
Hardcover book:
Chapra, S.C., and R.P. Canale. Numerical Methods for Engineers , 7th edition, McGraw Hill, 2015. (Optional)
Updated: 1/11/2021
Browse Course Material
Course info.
- Dr. Benjamin Seibold
Departments
- Mathematics

As Taught In
- Algorithms and Data Structures
- Numerical Simulation
- Differential Equations
- Mathematical Analysis
Learning Resource Types
Numerical methods for partial differential equations, project description and schedule.
The course project counts for 50% of the overall course grade.
The project consists of
- a midterm report (20% of the project grade)
- a final report (60% of the project grade), and
- a presentation (20% of the project grade)
Throughout the term, each participant works on an extended problem related to the content of the course. You are allowed to choose a project which is related to your thesis, however, the following restrictions apply:
- The project must focus on computational aspects related to the lecture topics.
- It is illegal to “reuse” a project from another course or thesis work. Your 8.336 project must cover specific questions and goals, which must not to be identical to the questions and goals of your thesis. For instance, you can investigate a specific computational aspect of your work, and investigate this aspect deeper than you would in your thesis work.
Of course, you can also choose a topic unrelated to your other work. For instance, you can consult the lecturer for interesting problems related to his research.
Any course project has to be agreed on by, and is under the supervision of the lecturer.
The following deadlines apply:
- By Ses #4: Submit project proposal
- By Ses #13: Submit midterm report on project
- By Ses #25: Submit final project report
- Last two sessions: Give short talk on project
Project Proposal
Your project proposal to should include the following information:
- Project title
- Project background Does it relate to your work in another field (e.g. your thesis)? If yes, briefly outline the questions and goals of your work in the other field.
- Questions and Goals Briefly describe the questions you wish to investigate in your project. What are your expectations?
- Plan Which language do you plan to program in? Do you intend to use special software? Does your project work relate to the work of other people at MIT?
Project Abstracts
Project presentations take place on a Saturday, and are aimed at a general scientific audience, with focus on the numerical solution of physically arising equations.
The following represents the project abstracts chosen by the students during the Spring ‘09 term.
Numerical Solution for Poisson Equation with Variable Coefficients
I will present a numerical technique to obtain the solution of a quasi-3-dimensional potential distribution due to a point source of current located on the surface of the semi-infinite media containing an arbitrary 2-dimensional distribution of conductivity. I will show how two different boundary conditions (Neumann and mixed) chosen to simulate the “infinitely distant” edges of the lower half-space affect the accuracy of the solution. The solution on the uniform and non-uniform grid will be compared. Some figures showing the potential field over the simple structures (such as layered media, vertical contact, square body) will be presented.
Finite Difference Elastic Wave Modeling with an Irregular Free Surface
The objective of my project is to model elastic wave propagation in a homogenous medium with surface topography. Surface topography and the weathered zone (i.e., heterogeneity near the earth’s surface) have great effects on seismic surveys as the recorded seismograms can be severely contaminated by scattering, diffractions, and ground rolls that exhibit non-ray wave propagation phenomena. implemented a 2-D staggered finite difference approximation of first order PDEs that is second-order accurate in time and space (with velocity-stress formulation), and described the results of the finite-difference scheme on various irregular free surface models.
Simulation of the Onset of Baroclinic Instability
Many features of atmospheric dynamics can be demonstrated with a simple table-top rotating tank experiment. Here a numerical simulation of the incompressible Navier-Stokes equations and the heat equation is applied to a flow in a rotating annular tank. A finite difference method is used on an axisymmetric 2-Drotating reference frame. At low rotational rates a stable vertical velocity gradient is observed in the zonal flow, corresponding to the tropical Hadley cell flow. At high rotational rates a baroclinic instability is observed, corresponding to atmospheric dynamics seen in the upper-latitudes.
Analysis of the Time-Dependent Coupling of Optical-Thermal Response of Laser-Irradiated Tissue Using Finite Difference Methods
Over the years lasers have been extensively used for detection and treatment of diseases and abnormal health conditions including cancerous tissues and arterial plaques. While such detection and treatment has numerous advantages including superior accuracy and unparalleled control over conventional techniques, it is imperative to optimize light dosimetry, treatment parameters and conditions of delivery a priori so that thermal damage due to laser irradiation is limited to the tissue area (volume) under consideration. In this work, a non-linear finite-difference program is developed to simulate the dynamic evolution of tissue coagulation considering the dependence of the optical properties and blood perfusion on the instantaneous temperature and damage index. Using this coupled optical diffusion-bioheat equation model, we observe that significant changes arise as a function of the dynamic behavior of the optical properties and the perfusion. Specifically, the model reveals that the heat penetration in laser irradiated tissue is much lesser than what would be expected from a static treatment of the biophysical parameters. Finally, we provide preliminary results on the optical-thermal response of the tissue on application of a pulsed laser.
Modeling and Simulation of Self-Sustained Combustions in Reactive Multi-Layers of Energetic Materials
It is known that forced mixing of energetic materials such as nickel and aluminum results in highly exothermic reactions. The reaction, herein combustion, initiated by thermal impulses propagates through the materials in self-sustained manner. In this project, self-sustained combustion and its propagation in a reactive Ni-Al nanolaminate is first mathematically modeled in two coupled partial differential equations for heat and atomic diffusions. The, the coupled governing equations are discretized in time and space, and numerically solved using the finite difference schemes for the Ni-Al nanolaminate domain with appropriate initial and boundary conditions for the temperature and atomic composition. The simulation results for the heat and mass diffusion with combustions would be presented, and compared with several experimental results. Also, several important effects of simulation conditions such as initial temperature profile, ambient temperature and Ni-Al premixed thickness would be discussed. Finally, several important features for the governing equations, and physical and chemical assumptions for the models would be addressed.
Simulation of an Airbag for Landing of Re-Entry Vehicles
This presentation will focus on the implementation of the Immersed Boundary Method to approximate the dynamics of an impacting airbag intended for use in Earth re-entry vehicle applications. Specifically, the numerical approach and its related implementation issues will be discussed, followed by a discussion and analysis of the obtained results.
Immersed Boundary Method (IBM) for the Navier Stokes Equations
Studying certain medical conditions, such as hypertension, requires accurate simulation of the blood flow in complex-shaped elastic arteries. In this work we present a 2-D fluid-structure interaction solver to accurately simulate blood flow in arteries with bends and bifurcations. Such blood flow is mathematically modeled using the incompressible Navier-Stokes equations. The arterial wall is modeled using a linear elasticity model. Our solver is based on the immersed boundary method (IBM). The numerical accuracy of our solver stems from using a staggered grid for the spatial discretization of the incompressible Navier-Stokes equations. The computational efficiency of our method stems from using Chorin’s projection method for the time stepping, coupled with the fast Fourier transform (FFT) to solve the intermediate Poisson equations. We have validated our results versus reference results obtained from MERCK Research Laboratories for a straight vessel of length 10cm and diameter 2cm. Our results for pressure, flow and radius variations are within 5% of those obtained from MERCK.
Finite Difference Modeling of Seismic Wave Propagation in Fractured Media (2D)
It is critical to detect and characterize fracture networks for production of oil reservoirs. Much effort has gone into the development of methods for identifying and understanding fracture systems from seismic data. Forward modeling of seismic wave propagation in fractured media plays a very important role in this field. In equivalent medium theory, background medium pluses fracture is equivalent to anisotropy medium, in this paper, I will use this theory together with staggered finite difference technique for modeling seismic wave propagation in fractured media.
Glacial Ice Streams
Two models of one-dimensional longitudinal glacial ice flow as a function of depth are presented. The system dynamics are governed by Stokes? 2019 flow acting under the influence of a velocity dependent viscosity coefficient. The domain of computation is discretized on a staggered one-dimensional grid to enhance the stability of the methods. The first model uses a centered finite difference scheme to treat the problem as a diffusion problem with non-constant spatially and temporally varying coefficients. The second model combines centered and upwinded finite difference schemes to treat the problem as an advection problem. These methods are compared for a range of basal boundary conditions representative of the found in large glacial ice sheets, with prescribed velocities, shear stresses, or shear stress limits.
Solver for Axisymmetric Low Speed Inviscid Flow
A blade row refers to a set of airfoils attached circumferentially to a central hub. The blades and hub may be stationary (stator) or rotating (rotor) and each such arrangement forms a stage of turbomachinery systems. These systems include compressors, turbines, pumps, propellers and fans and have crucial applications in all aspects of engineering. This project addresses reduced order modeling of the 3d flow characteristics of a low speed axisymmetric blade row in the 2d meridional reference frame. The approach is to implement a finite difference discretization of the 2d domain and represent the effect of the blades using a postulated blade loading model (local forcing term). However, the iterative solver for the large non-linear 3x3 system proved very difficult to implement in the finite difference setting being very prone to implementation errors. Accuracy of the blade loading model was also hard to quantify due to the complexity involved with higher order spatial discretization.
Modeling the Process of Milk Steaming by an Espresso Machine
In this project the insulating properties of a ceramic mug and an aluminum mug are compared. The Heat Transfer equation is solved over the systems as to compare the speed at which heat is lost from the beverage. The radial symmetry of the system is employed to simplify the calculation from a 3 dimensional physical space to a 2 dimensional cylindrical system without rotation. The complications arising from the 1/ r term in the cylindrical form of the Heat Transfer equation is discussed and resolved. Additionally, a predictive model is developed to determine the temperature of a cup of coffee at a certain time, t , given the vessel’s material and the percentage of milk in the coffee.
Numerical Solution of the Continuous Linear Bellman Equation
Solutions to the Hamilton-Jacobi-Bellman (HJB) equation describe an optimal policy for controlling a dynamical system such as a robot or a virtual character. However, the HJB equation is a non-linear PDE that is difficult to solve directly, especially for stochastic systems. For a certain class of optimal control problems, a change of variables turns the non-linear Hamilton-Jacobi-Bellman (HJB) equation into a linear PDE. This PDE, the linear Bellman equation, can be solved analytically in certain cases and numerically using standard methods in other cases. As an example application, one can use solutions of the linear Bellman equation to navigate a three wheeled robot.

You are leaving MIT OpenCourseWare

Latest Projects Based on Numerical Methods
The following projects are based on numerical methods. This list shows the latest innovative projects which can be built by students to develop hands-on experience in areas related to/ using numerical methods.
1. A Numerical Solution to 2D Flat Plate Problem with Constant Conductivity Heat Transfer
All the engineering devices we use involves the conversion of energy. In this process, a lot of heat released to the surroundings as a part of energy loss. The efficiency of any device can be increased by minimizing loss due to heat transfer. That’s why a lot of research going on around the world in the field of heat transfer. To solve real-life heat transfer problems Numerical methods are preferred, because of less time consumption, ease, and convenience. To get hands-on experience on numerical methods, here you are going to solve the Two-Dimensional flat plate problem with Constant conductivity heat transfer by using Numerical methods.
2. A Numerical Solution to One Dimensional Conductive Heat Transfer with Constant Conductivity
Numerical analysis is one of the most researched fields today. Getting an exact solution for physical problems is too difficult and again for most of the physical problems exact solution does not exist at all, so numerical techniques are preferred to obtain a fairly exact solution with ease. In this project, you will write your own codes to simulate temperature distribution over a 1D flat plate and compare its result with the exact solution to check the accuracy of your Numerical solution.
3. A Numerical solution to One Dimensional Conductive Heat Transfer with Variable Conductivity
4. understanding fvm(lax friedrich scheme) by solving burger equation.
Finite Volume Method is one of the popular numerical methods used by engineers, mathematicians around the world for solving complex differential equations. This is because it has the characteristics to produce accurate and stable solutions. So, studying the finite volume method is important for an engineer. In this project, you will learn how the Finite Volume Method (Numerical Method) is implemented to solve the differential equation by solving a fluid flow problem using Burger equation.
5. A Numerical Study on Different Types of Fins
Fin is nothing but an extended surface found on the heat exchanging devices such as radiators in Car, Bike engines, Computer CPU heatsinks and Heat exchangers in power plants. An efficient Fin can really increase the performance of a system. There are various types of Fin and analyzing those theoretically takes a lot of effort. So, researchers around the world take help of numerical methods to analyze complex problem such as heat transfer through Fin. In this project, you will work on solving the various type of fin using numerical methods and compare it with a theoretical solution where it exists.
Build projects on latest technologies
Want to develop practical skills on latest technologies? Checkout our latest projects and start learning for free
6. Analysis of Turbulence in a Two Dimensional Cavity Flow
Turbulent flows have an infinite variety ranging from the flow of blood in our body to the atmospheric flows. Everyday life gives us an intuitive knowledge of turbulence in fluids; during air travel, one often hears the word turbulence generally associated with the fastening of seat-belts. The flow passing an obstacle or an airfoil creates turbulence in the boundary layer and develops a turbulent wake which will generally increase the drag exerted by the flow on the obstacle. The majority of atmospheric or oceanic currents cannot be predicted accurately and fall into the category of turbulent flows, even in the large planetary scales. Galaxies look strikingly like the eddies which are observed in turbulent flows such as the mixing layer, and are, in a way of speaking, the eddies of a turbulent universe. Numerous other examples of turbulent flows arise in aeronautics, hydraulics, nuclear and chemical engineering, oceanography, meteorology, astrophysics, and internal geophysics. A clear understanding of this physical phenomena is one of the most essential and important problems of applied science.
7. Numerical simulation of wind flow
Wind is a random phenomenon because of the many flow situations arising from the interaction of wind with structures. The turbulence of strong winds in the lower levels of the atmosphere arises from interaction with surface features. An outcome of the turbulence is that dynamic loading on a structure depends on the size of eddies. Large eddies, comparable with the structure introduces correlated pressure as they envelope with the structure.
8. FEM with HyperWorks
You can build this project at home. You can build the project using online tutorials developed by experts. 1-1 support in case of any doubts. 100% output guaranteed. Get certificate on completing.
Latest Projects based on numerical methods
Any questions.
Join 250,000+ students from 36+ countries & develop practical skills by building projects
Get kits shipped in 24 hours. Build using online tutorials.
Subscribe to latest project ideas
Stay up-to-date and build projects on latest technologies
☎ Have a Query?
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
Real-Life Applications of Numerical Analysis
Numerical analysis is the study of algorithms that solve mathematical problems numerically. It is a powerful tool in many fields. From weather forecasting to financial markets, it has many applications. Engineers use it to design safer buildings and vehicles.

Health professionals depend on it for clearer medical images. It plays a role in safeguarding our digital communications too. In this article, we are going to learn about various real-life applications of numerical analysis in detail.
What is Numerical Analysis?
Numerical analysis is a branch of mathematics that deals with algorithms for solving numerical problems. These problems come from real-world applications where exact solutions are difficult or impossible to find analytically. This field focuses on finding approximate solutions and understanding how accurate these solutions are.
For example, when predicting weather, numerical analysis helps in simulating atmospheric conditions over time. It calculates temperature, wind speed, and humidity across different geographic locations.
Applications of Numerical Analysis
Numerical analysis plays a crucial role in modern science and engineering. It helps solve problems that are too complex for analytical methods.
Here are some real-life applications of numerical analysis:
Weather Forecasting
Predicting weather involves complex calculations. Numerical analysis simplifies these into manageable tasks.
- Meteorologists use numerical models to predict weather patterns. These models calculate temperature, wind, and humidity across different locations and times.
- The accuracy of weather predictions relies on solving differential equations. These equations describe how atmospheric conditions change.
- Numerical methods help in simulating hurricanes, tornadoes, and other extreme weather events. This aids in disaster preparedness and response strategies.
- By refining these models, predictions become more reliable. This leads to better planning for agriculture, travel, and emergency services.
Engineering Design
Engineers design structures and machines using numerical analysis. It ensures safety and efficiency.
- Structural analysis, like determining the stress on a bridge, uses numerical methods. This helps ensure the bridge can withstand load and stress.
- In aerospace, numerical analysis simulates airflow around aircraft. This is crucial for designing safer and more efficient aircraft.
- Automobile engineers use it to improve fuel efficiency and safety features in vehicles.
- These methods reduce the need for physical prototypes. This saves time and money in the design process.
Financial Modeling
Financial markets use numerical analysis for pricing options and managing risk.
- Algorithms calculate the future value of stocks and bonds. This helps investors make informed decisions.
- Numerical analysis also predicts economic trends by analyzing historical data.
- It helps in assessing risk and expected returns, essential for portfolio management.
- This analysis supports the development of automated trading systems, enhancing market efficiency.
Image Processing
Image processing uses numerical methods to improve digital images. This has applications in various fields.
- Medical imaging, like MRI and CT scans, relies on these techniques to provide clear images. This is vital for accurate diagnosis.
- In astronomy, it enhances images of celestial bodies, helping scientists study distant planets and stars.
- Numerical analysis also powers facial recognition technology used in security systems.
- It is essential in the entertainment industry for creating high-resolution graphics and special effects.
Drug Development
Pharmaceutical companies use numerical analysis to speed up drug development. It makes the process more efficient.
- By simulating drug interactions at the molecular level, researchers can predict the effectiveness of a drug.
- Numerical models help understand the behavior of new drugs in the human body. This reduces the need for extensive clinical trials.
- It also helps in designing controlled release medications that improve patient compliance and treatment effectiveness.
- These methods enable researchers to explore more potential treatments in less time.
Environmental Science
Numerical analysis helps in solving environmental issues. It helps in understanding and protecting our environment.
- It models pollution dispersion in air, water, and soil. This is crucial for environmental protection.
- Climate models use numerical methods to predict changes in climate. This is important for developing strategies to mitigate climate change.
- It also assists in managing natural resources, like water and forests, more sustainably.
- These models help in assessing the impact of human activities on ecosystems, guiding conservation efforts.
Cryptography
Cryptography ensures secure communication. Numerical analysis is key in developing encryption methods.
- It is used to create algorithms that protect data from unauthorized access.
- Numerical methods help in the analysis of cryptographic algorithms to ensure they are secure.
- They are essential in developing new encryption techniques that are harder to break.
Seismic Data Analysis
Numerical analysis helps understand seismic activities to mitigate disaster risks. It plays an important role in geology and civil engineering.
- Geophysicists use numerical models to simulate earthquake scenarios. This helps in assessing the potential impact on buildings and infrastructure.
- By analyzing seismic data, scientists can better predict the likelihood of future earthquakes. This is crucial for disaster preparedness.
- Numerical methods aid in the design of earthquake-resistant structures, enhancing safety and minimizing damage.
- They also contribute to the exploration of oil and gas by interpreting seismic data to locate reserves.
Power Systems Engineering
The stability and efficiency of power grids depend heavily on numerical analysis.
- Engineers use numerical techniques to model and simulate the behavior of electrical grids. This ensures stability and efficient power distribution.
- Numerical methods help in optimizing the operation of renewable energy sources like wind turbines and solar panels.
- They are crucial for designing systems that integrate various types of energy sources, maintaining a stable energy supply.
- These methods also support the development of smart grids, which automatically respond to changes in energy demand and supply.
Robotics integrates numerical analysis to enhance functionality and autonomy.
- In robotics, numerical methods are used for motion planning and control. This allows robots to move efficiently and perform tasks accurately.
- Numerical simulations help engineers test robotic systems under different scenarios before actual deployment.
- They are essential in developing algorithms that enable robots to learn from their environment and adapt to new tasks.
FAQs on Applications of Numerical Analysis
What is numerical analysis used for in finance.
Numerical analysis is crucial in finance for pricing derivatives, optimizing investment portfolios, and assessing financial risks. It enables precise calculations for better decision-making in markets.
How does numerical analysis benefit weather forecasting?
In weather forecasting, numerical analysis helps predict weather patterns by solving complex atmospheric equations. This enhances the accuracy of weather predictions, aiding in disaster management and agricultural planning.
Can numerical analysis improve engineering designs?
Yes, numerical analysis is vital in engineering for simulating and analyzing stress, dynamics, and fluid flows in structures and systems. This ensures safer, more efficient designs and reduces the need for physical prototypes.
What role does numerical analysis play in healthcare?
Numerical analysis is used extensively in healthcare, especially in medical imaging and drug development. It improves the clarity of diagnostic images and simulates drug interactions to predict effectiveness and side effects.
How is numerical analysis applied in environmental science?
It models pollution dispersion, climate change, and resource management, helping scientists predict environmental impacts and develop sustainable practices. Numerical analysis is essential for informed environmental policymaking and conservation efforts.
What is the importance of numerical analysis in cryptography?
Numerical analysis is fundamental in developing and testing encryption algorithms. It ensures secure data transmission, protects against unauthorized access, and is crucial for maintaining privacy in digital communications.
Please Login to comment...
Similar reads.
- School Learning
- Real Life Application
- How to Get a Free SSL Certificate
- Best SSL Certificates Provider in India
- Elon Musk's xAI releases Grok-2 AI assistant
- What is OpenAI SearchGPT? How it works and How to Get it?
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Open access
- Published: 22 August 2024
Numerical model of debris flow susceptibility using slope stability failure machine learning prediction with metaheuristic techniques trained with different algorithms
- Kennedy C. Onyelowe 1 , 2 , 3 ,
- Arif Ali Baig Moghal 4 ,
- Furquan Ahmad 5 ,
- Ateekh Ur Rehman 6 &
- Shadi Hanandeh 7 , 8
Scientific Reports volume 14 , Article number: 19562 ( 2024 ) Cite this article
27 Accesses
Metrics details
- Civil engineering
- Natural hazards
In this work, intelligent numerical models for the prediction of debris flow susceptibility using slope stability failure factor of safety (FOS) machine learning predictions have been developed. These machine learning techniques were trained using novel metaheuristic methods. The application of these training mechanisms was necessitated by the need to enhance the robustness and performance of the three main machine learning methods. It was necessary to develop intelligent models for the prediction of the FOS of debris flow down a slope with measured geometry due to the sophisticated equipment required for regular field studies on slopes prone to debris flow and the associated high project budgets and contingencies. With the development of smart models, the design and monitoring of the behavior of the slopes can be achieved at a reduced cost and time. Furthermore, multiple performance evaluation indices were utilized to ensure the model’s accuracy was maintained. The adaptive neuro-fuzzy inference system, combined with the particle swarm optimization algorithm, outperformed other techniques. It achieved an FOS of debris flow down a slope performance of over 85%, consistently surpassing other methods.
Similar content being viewed by others

Prediction of slope failure in open-pit mines using a novel hybrid artificial intelligence model based on decision tree and evolution algorithm
Real-time prediction of Poisson’s ratio from drilling parameters using machine learning tools
Application of classical and novel integrated machine learning models to predict sediment discharge during free-flow flushing
Introduction.
Analytical studies on debris flow susceptibility typically involve the use of various methods to assess and predict the potential for debris flow in a given area 1 , 2 . These studies aim to understand the factors that contribute to the initiation, magnitude, and runout of debris flows, as well as the susceptibility of specific locations to these hazardous events 3 . Several analytical methods and approaches are commonly used in these studies, including geomorphological mapping (GM), which involves the identification and analysis of landforms, surface materials, and landscape features associated with previous debris flows 4 . This approach helps in understanding the spatial distribution of potential debris flow source areas and their associated susceptibility factors 5 . Hydrological and hydraulic modeling (HHM): Analytical studies often utilize hydrological and hydraulic modeling to simulate rainfall-runoff processes and the behavior of flowing debris 6 . These models can help identify areas at risk of debris flow initiation and estimate potential flow paths and runout areas 7 . Geotechnical and geophysical investigations (GGI) involve the assessment of soil properties, subsurface conditions, and the mechanical behavior of materials in potential debris flow source areas 8 . This can include laboratory testing, in situ measurements, and geophysical surveys to evaluate the susceptibility of slopes to failure and debris flow initiation 9 . Statistical and probabilistic approaches are used to quantify the relationships between debris flow occurrence and various influencing factors, such as rainfall intensity, land cover, slope gradient, and geological characteristics 10 . Probabilistic models may be developed to assess the likelihood of debris flow events under different conditions 11 . Remote sensing and geographic information systems (RSGIS): Remote sensing data, including aerial and satellite imagery, as well as GIS-based analyses, are often employed to identify and map terrain characteristics, land cover, and hydrological features associated with debris flow susceptibility 12 . Field surveys and case studies (FSCS) provide valuable data on past debris flow events, including their triggers, characteristics, and impacts 13 . These studies contribute to the development of empirical relationships and the validation of predictive models 14 . By integrating these analytical approaches, researchers and practitioners can develop comprehensive assessments of debris flow susceptibility, leading to improved hazard mapping, risk management strategies, and early warning systems 15 . These studies are essential for understanding the complex interactions between geological, hydrological, and environmental factors that influence debris flow occurrence and for guiding land use planning and disaster risk reduction efforts 16 .
Numerical simulation of debris flow susceptibility involves the use of computational models and simulations to assess and predict the potential for debris flows in specific areas 17 . These simulations aim to capture the complex interactions between various factors that influence debris flow initiation, propagation, and runout 18 . Several numerical modeling techniques are commonly used for simulating debris flow susceptibility, including HHM, which utilizes numerical models to simulate rainfall-runoff processes and the behavior of flowing debris. This approach is essential for assessing debris flow susceptibility 7 . These models typically consider factors such as rainfall intensity, soil moisture, topography, and channel characteristics to predict the likelihood and magnitude of debris flow events 3 . Geotechnical modeling: Numerical simulations can be used to model the mechanical behavior of slopes and the initiation of debris flows under different conditions. These models consider factors such as soil properties, slope stability, and the influence of pore water pressure on slope failure, providing insights into the susceptibility of specific areas to debris flows 11 . Coupled hydromechanical models (CHMs) integrate the hydraulic and mechanical aspects of debris flows, accounting for the interactions between water, sediment, and the surrounding terrain. They simulate the transient behavior of debris flows, including their initiation, flow dynamics, and deposition, considering the influence of slope geometry and soil properties 15 . Particle-based models: Some numerical simulations use particle-based methods to represent the behavior of individual sediment particles and the flow of debris 9 . These models can capture the granular nature of debris flows and their interactions with the surrounding terrain, providing insights into susceptibility factors such as flow velocity, inundation area, and impact forces. Probabilistic and statistical models (PSM): Numerical simulations can incorporate probabilistic and statistical approaches to assess debris flow susceptibility 16 . These models consider uncertainties in input parameters and help quantify the likelihood of debris flow occurrence under different scenarios, aiding in risk assessment and hazard mapping. Three-dimensional (3D) geomorphic modeling (TDGM): Advanced numerical simulations can utilize 3D geomorphic models to simulate the complex topography and terrain features that influence debris flow susceptibility 17 . These models can capture the spatial distribution of susceptibility factors and provide detailed simulations of debris flow behavior in complex landscapes 18 . By employing these numerical modeling techniques, researchers and practitioners can gain insights into the factors that contribute to debris flow susceptibility and develop predictive tools to assess the potential impact of debris flows in specific areas 17 . These simulations are valuable for informing land use planning, disaster risk reduction strategies, and the development of early warning systems for debris flow hazards.
The mathematics of debris flows down a slope involves the application of the fundamental principles of fluid mechanics, solid mechanics, and granular flow to describe the behavior of the mixture of water, soil, and rock as it moves downslope 3 . While the specific mathematical models can be quite complex, it is useful to consider a simplified overview of the key mathematical aspects involved in understanding debris flows down a slope. Conservation laws: The conservation of mass and momentum are fundamental principles that underlie the mathematical modeling of debris flows 7 . These laws are expressed through partial differential equations (PDEs). For example, the continuity equation represents the conservation of mass, and the Navier–Stokes equations describe the conservation of momentum for the fluid phase 8 . Constitutive relationships: Debris flows are typically non-Newtonian fluids due to the presence of solid particles 10 . The constitutive relationships describe the rheological behavior of the debris flow material, including the interaction between the fluid phase and the solid particles 11 . These relationships can be quite complex and may involve empirical or semi-empirical models to capture the behavior of the mixture. Granular flow modeling: Due to the presence of solid particles, the debris flow may exhibit characteristics of granular flow 12 . Models such as the Coulomb-Mohr yield criterion and the Drucker-Prager model are often used to capture the behavior of granular materials and their interaction with the fluid phase. Slope stability analysis: The mathematics of debris flows down a slope often involves considerations of slope stability and the initiation of the flow 13 . This can include the application of soil mechanics principles, such as the Mohr–Coulomb criterion, to assess the stability of the slope and predict the conditions under which debris flows may occur. Runout modeling: Debris flows exhibit complex runout behavior as they travel downslope 19 . Mathematical models, such as depth-averaged models or more detailed computational fluid dynamics (CFD) simulations, can be used to predict the runout distance and behavior of the debris flow based on the properties of the material and the slope geometry 6 . Numerical simulations: Advanced numerical methods, including the finite element method (FEM), finite volume method (FVM), or discrete element method (DEM), can be used to simulate the behavior of debris flows down a slope 17 . These simulations involve discretizing the governing equations and solving them numerically to predict the flow behavior 5 . It is important to note that the mathematical modeling of debris flows down a slope is a highly interdisciplinary field, drawing on principles from fluid mechanics, solid mechanics, and geotechnical engineering 19 . The actual mathematical models used to describe debris flows can vary in complexity, ranging from simple empirical relationships to sophisticated multiphase flow models, and are often tailored to specific site conditions and phenomena.
Finite element modeling can be a valuable tool for assessing debris flow susceptibility, particularly in the context of understanding the mechanical behavior of the underlying terrain and the potential for debris flow initiation 19 , 20 . When using finite element modeling to assess debris flow susceptibility, several aspects are considered. Geotechnical properties: Finite element modeling allows for the incorporation of geotechnical properties of soil and rock masses, including factors such as shear strength, cohesion, internal friction angle, and permeability 21 . These properties play a critical role in determining the stability of slopes and the potential for debris flow initiation. Slope stability analysis: Finite element models can be used to perform slope stability analyses, considering the influence of various factors, such as slope geometry, soil properties, groundwater conditions, and seismic loading 5 , 22 . These analyses can help identify areas of potential instability and assess the susceptibility of slopes to failure and subsequent debris flow generation. Coupled hydromechanical modeling: Finite element models can be coupled with hydraulic analyses to simulate the interactions between water and soil within the slope 23 . This allows for the assessment of pore water pressure development, the influence of rainfall or rapid snowmelt on slope stability, and the potential for liquefaction and debris flow initiation. Debris flow initiation: Finite element modeling can be used to simulate the conditions under which debris flow initiation may occur 24 . This includes evaluating the influence of rainfall, pore water pressure changes, and other triggering factors on the mechanical stability of slopes and the potential for mass movement. Material failure and runout analysis: Finite element modeling can be employed to simulate the failure and movement of soil and debris masses, including the mechanics of mass movement, runout distances, and impact forces 13 . This can provide insights into the potential extent and impact of debris flows in susceptible areas 14 . Sensitivity analyses: Finite element models can be used to conduct sensitivity analyses to assess the influence of different parameters on debris flow susceptibility 15 . This can help identify critical factors that contribute to the potential for debris flow initiation and propagation 4 . By utilizing finite element modeling techniques to assess debris flow susceptibility, researchers and practitioners can gain a better understanding of the geotechnical and hydraulic factors that influence the potential for debris flows 10 . These models can aid in the identification of high-risk areas, the development of mitigation strategies, and the implementation of measures to reduce the impact of debris flows on human settlements and infrastructure.
The mathematical formulation of a debris flow problem using the FEM involves the description of the governing equations, boundary conditions, and material properties in a way that can be discretized and solved using finite element techniques 19 . Debris flows are complex phenomena involving the interaction of solid particles and fluid, and their mathematical modeling often requires the use of advanced numerical methods, such as the FEM 22 . The governing equations for a debris flow problem typically include the conservation of mass, momentum, and possibly energy 24 . In the case of a two-phase flow involving solid particles and fluid, the governing equations may include the Navier–Stokes equations for the fluid phase, coupled with equations describing the motion of the solid particles 25 . Constitutive equations are used to describe the behavior of the debris flow material, including the rheological properties of the fluid phase and the interaction between the solid particles and the fluid 6 . These constitutive equations may include models for viscosity, granular flow, and other relevant material properties 26 . Boundary conditions define the conditions at the boundaries of the computational domain, including inlet and outlet conditions for the flow, as well as any solid boundaries that may affect the flow behavior 26 , 27 , 28 . Discretization: The next step is to discretize the governing equations and boundary conditions using the FEM 27 . This involves subdividing the computational domain into a mesh of elements, defining the basis functions for representing the solution within each element, and then assembling the governing equations into a system of algebraic equations 24 . Solution: The system of algebraic equations is then solved numerically to obtain the solution for the debris flow problem 5 , 11 , 18 . This may involve the use of iterative solution techniques and time-stepping methods for transient problems 5 . Validation and post-processing: Finally, the computed solution is validated against experimental or observational data, and post-processing techniques are used to analyze the results and extract relevant information about the debris flow behavior, such as flow velocities, pressures, and particle trajectories 12 . It is important to note that the specific mathematical formulation for a debris flow problem using the FEM will depend on the particular characteristics of the problem, such as the properties of the debris flow material, the geometry of the flow domain, and the boundary conditions 15 . Additionally, advanced modeling techniques, including multiphase flow and fluid–structure interaction, may be necessary to accurately capture the behavior of debris flows.
Moreno, Dialami, and Cervera 27 specifically examined the numerical modeling of spillage and debris floods. The flows are classified as either Newtonian or viscoplastic Bingham flows, and they involve a free surface. The modeling approach utilized mixed stabilized finite elements. This study introduced a Bingham model with double viscosity regularization and presented a simplified Eulerian approach for monitoring the movement of the free surface. The numerical solutions were compared to analytical, experimental, and results from the literature, as well as field data obtained from a genuine case study. Quan Luna et al. 28 developed physical vulnerability curves for debris flows by utilizing a dynamic run-out model. The model computed tangible results and identified areas where vulnerable components may experience an adverse effect. The study used the Selvetta debris flow event from 2008, which was rebuilt following thorough fieldwork and interviews. This study measured the extent of physical harm to impacted buildings in relation to their susceptibility to damage, which is determined by comparing the cost of damage with the value of reconstruction. Three distinct empirical vulnerability curves were acquired, showcasing a quantitative method to assess the susceptibility of an exposed building to debris flow, regardless of when the hazardous event takes place. According to Nguyen, Tien, and Do 29 , landslides in Vietnam frequently transpire on excavated slopes during the rainy season, necessitating a comprehensive understanding of influential elements and initiating processes. This study investigates the most significant deep-seated landslide that occurred because of intense precipitation on July 21, 2018 and the subsequent sliding of the Halong-Vandon expressway. The results indicated that heavy rainfall is the primary component that triggers landslides, while slope cutting is identified as the key causative cause. The investigation also uncovered human-induced impacts, such as inaccurate safety calculations for road construction and quarrying activities, which led to the reactivation of the landslide body on the lower slope due to the dynamic effect of subsequent sliding. Bašić et al. 30 presented Lagrangian differencing dynamics (LDD), a method that utilized a meshless and Lagrangian technique to simulate non-Newtonian flows. The method employed spatial operators that are second-order consistent to solve the generalized Navier–Stokes equations in a strong formulation. The solution was derived using a split-step approach, which involved separating the pressure and velocity solutions. The approach is completely parallelized on both CPU and GPU, guaranteeing efficient computational time and allowing for huge time steps. The simulation results are consistent with the experimental data and will undergo validation for non-Newtonian models. Ming-de 31 described a finite element analysis of the flow of a non-Newtonian fluid in a two-dimensional (2D) branching channel. The Galerkin method and mixed FEM were employed. In this case, the fluid is regarded as an incompressible, non-Newtonian fluid with an Oldroyd differential-type constitutive equation. The non-linear algebraic equation system, defined using the finite element approach, was solved using the continuous differential method. The results demonstrated that the FEM is appropriate for analyzing the flow of non-Newtonian fluids with intricate geometries. Lee et al. 32 analyzed the effects of erosion on debris flow and impact area using the Deb2D model, developed in Korea. The research was conducted on the Mt. Umyeon landslide in 2011, comparing the impacted area, total debris flow volume, maximum velocity, and inundated depth from the erosion model with field survey data. The study also examined the effect of entrainment changing parameters through erosion shape and depth. The results showed the necessity of parameter estimation in addressing the risks posed by shallow landslide-triggered debris flows. Kwan, Sze, and Lam 33 employed numerical models to simulate rigid and flexible barriers aimed at reducing the risks associated with boulder falls and debris flows in landslide-prone areas. The performance of cushioning materials, such as rock-filled gabions, recycled glass cullet, cellular glass aggregates, and EVA foam, was evaluated. Finite element models were created to replicate the interaction between debris and barriers. These models showed a reduced hydrodynamic pressure coefficient and negligible transfer of debris energy to the barrier. Martinez 34 developed a 3D numerical model for the simulation of stony debris flows. The model considered a fluid phase consisting of water and fine sediments, as well as a non-continuum phase consisting of big particles. The model replicated interactions between particles and between particles and walls, incorporating Bingham and Cross rheological models to represent the behavior of the continuous phase. It exhibited stability even under low shear rates and is capable of handling flows with high particle density. It is useful for strategizing and overseeing regions susceptible to debris movement. Martinez, Miralles-Wilhelm, and Garcia-Martinez 35 presented a 2D debris flow model that utilized non-Newtonian Bingham and Cross rheological formulations. This model considered variations in fluid viscosity and internal friction losses. The model underwent testing for dam break scenarios and demonstrated strong concurrence with empirical data and analytical solutions. The model yielded consistent outcomes even when subjected to low shear rates, thus preventing any instability in non-continuous constitutive relationships.
According to Nguyen, Do, and Nguyen 36 , landslides present a worldwide risk, especially in areas with high elevation. A profound landslide transpired close to the Mong Sen bridge in Sapa town, located in the Laocai province of Vietnam. The fissures were a result of incisions made during the process of road construction. The investigation determined that cutting operations were a contributing factor to the sliding of the sloped soil mass. The rehabilitation efforts involved excavating the soil above the original slope and building a retaining structure to stabilize the slope. According to Negishi et al. 37 , the Bingham fluid simulation model was formulated using the moving particle hydrodynamics (MPH) technique, which is characterized by physical consistency and adherence to fundamental rules of physics. The model accurately simulated the halting and solid-like characteristics of Bingham fluids, while also accounting for the preservation of linear and angular momentum. The method was confirmed and authenticated by doing calculations on 2D Poiseuille flow and 3D dam-break flow and then comparing the obtained results with theoretical predictions and experimental data. Kondo et al. 38 introduced a particle method that is physically consistent and specifically designed for high-viscosity free-surface flows, aiming to overcome the constraints of current methods. The method is validated through experimentation in a revolving circular pipe, high-viscous Taylor-Couette flights, and offset collision scenarios. This validation assures that the fundamental principles of mass, momentum, and thermodynamics are upheld, preventing any abnormal behavior in high-viscous free-surface flows. Sváček 39 focused on the numerical approximation of the flow of non-Newtonian fluids with a free surface, specifically in the context of new concrete flow. This work primarily examined the mathematical formulation and discretization of industrial mixes, which frequently exhibit non-Newtonian fluid behavior with regard to yield stress. This study employed the finite element approach for this purpose. Licata and Benedetto 40 introduced a computational method for modeling debris flow, specifically focused on simulating the consistent movement of heterogeneous debris flow that is constrained laterally. The proposed computational scheme utilized geological data and methodological ideas derived from simulations using cellular automata and grid systems. This scheme aimed to achieve a balance between global forecasting capabilities and computational resources. Qingyun, Mingxin, and Dan 41 examined the influence of debris flow and its ability to carry and incorporate silt in the beds of gullies located in hilly regions. The work used elastic–plastic constitutive equations and numerical simulations to investigate the coupling contact between solid, liquid, and structural components using a coupled analytical method. The model's viability was confirmed by a comparison of simulated results with empirical data. The study also investigated the impact of characteristics linked to the shape of debris on the process of erosion and entrainment in debris flow. Bokharaeian, Naderi, and Csámer 42 employed the Herschel-Buckley rheology model and smoothed particle hydrodynamics (SPH) approach to replicate the behavior of a mudflow on a free surface when subjected to a gate. The run-out distance and velocity were determined by numerical simulation and subsequently compared to the findings obtained in the laboratory. The findings indicated that the computer model exhibited a more rapid increase in run-out and viscosity compared to the experimental model, mostly due to the assumption of negligible friction. The use of an abacus is advised for simulating mudflows and protecting against excessive run-out distance and viscosity. Böhme and Rubart 43 presented an FEM for solving stable incompressible flow problems in a modified Newtonian fluid. The system employed a variational approach to express the equations of motion, with continuity being treated as a secondary requirement. The inertia term was discretized using finite elements, which led to the emergence of a nonlinear additional stress factor. According to Rendina, Viccione, and Cascini 44 , flow mass motions are highly destructive events that result in extensive destruction. Examining alterations in motion helps to comprehend the progression phases and construction of control measures. This study utilized numerical algorithms based on a finite volume scheme to examine the behavior of Newtonian and non-Newtonian fluids on inclined surfaces. The Froude number offers a distinct characterization of flow dynamics, encompassing the heights and velocities of propagation. The case studies mostly examined dam breaks in one-dimensional (1D) and 2D scenarios. Melo, van Asch, and Zêzere 45 used a simulation model to replicate the movement of debris flow and determine the rheological properties, along with the amount of rainfall beyond what is necessary. A dynamic model was employed, which was validated using 32 instances of debris flows. Under the most unfavorable circumstances, it was projected that 345 buildings might be affected by flooding. We have identified six streams that have been previously affected by debris flow and have suffered harm as a result. Reddy et al. 46 presented a finite element model that utilized the Navier–Stokes equations to simulate the behavior of unstable, incompressible, non-isothermal, and non-Newtonian fluids within 3D enclosures. The system employs power-law and Gtrreau constitutive relations, along with Picard's approach to solving non-linear equations. The model was utilized for the analysis of diverse situations and can be adapted for alternative constitutive relationships. Woldesenbet, Arefaine, and Yesuf 47 determined the geotechnical conditions and soil type that contribute to the onset of landslides. They also analyzed slope stability and proposed strategies to mitigate the associated risks. The measurement of slope geometry, landslide magnitude, and geophysical resistivity was conducted using fieldwork, laboratory analysis, and software analysis. The results indicated the presence of fine-grained soil, which had an impact on the qualities of the soil. The stability of a slope is influenced by various factors, such as the type of soil, the presence of surface and groundwater, and the steepness of the slope. For the purpose of ensuring stability, it is advisable to make alterations to the shape of the slope, construct retaining walls, improve drainage systems, and cultivate vegetation with deep root systems. Hemeda 48 examined the Horemheb tomb (KV57) in Luxor, Egypt, employing the PLAXIS 3D program for analysis. The failure loads were derived from laboratory experiments, and the structure was simulated using finite element code to ensure precise 3D analysis of deformation and stability. The elastic–plastic Mohr–Coulomb model was employed as a material model, incorporating factors such as Young's modulus, Poisson's ratio, friction angle, and cohesion. Numerical engineering analysis includes the assessment of the surrounding rocks, the estimation of elements influencing the stability of a tomb, and the integration of 3D geotechnical models. The study also examined therapeutic and retrofitting strategies and approaches, as well as the necessity for fixed monitoring and control systems to enhance and secure the cemetery. It also examined methods for treating rock pillars and implementing ground support strategies. Böhme and Rubart 43 introduced a finite element model for solving stable incompressible flow problems in a modified Newtonian fluid. The method employed a variational version of the equations of motion and utilized a penalty function approach to discretize the inertia term. The program emulated the shift from plug flow to pipe flow and yielded numerical outcomes for different Weissenberg values and constant Reynolds numbers. Whipple 49 studied the numerical simulation of open-channel flow of Bingham fluids, providing enhanced capabilities for evaluating muddy debris flows and associated deposits. The findings are only relevant to debris flows that contain a significant amount of mud. The numerical model used (FIDAP) enables the application and expansion of analytical solutions to channels with any cross-sectional shape while maintaining a high level of accuracy. The outcomes restrict the overall equations for discharge and plug velocity, which are appropriate for retroactive computation of viscosity based on field data, engineering analysis, and incorporation into debris-flow routing models in one and two dimensions. Rendina, Viccione, and Cascini 44 used numerical methods based on a finite volume framework to compare the behavior of Newtonian and non-Newtonian fluids on inclined surfaces. The Froude number offers a distinct characterization of flow dynamics, encompassing the heights and velocities of propagation. Case studies primarily concentrated on dam breach scenarios. Averweg et al. 50 introduced a least-squares FEM (LSFEM) for simulating the steady flow of incompressible non-Newtonian fluids using Navier–Stokes equations. The LSFEM provides benefits compared to the Galerkin technique, including the use of a posteriori error estimator and improved efficiency through adaptive mesh modifications. This approach expands upon the initial first-order LS formulation by incorporating the influence of nonlinear viscosity on fluid shear rate. It explored the Carreau model and used conforming discretization for accurate approximation. The reviewed resources from previous studies presented in Tables 1 and 2 show the current progress in the field, as well as the experimental requirements for the determination of the slope factor of safety (FOS). This requires sophisticated technology, which needs significant funding, technical services, and contingencies to determine the shear parameters (friction and cohesion), unit weight, pore pressure, and geometry of the studied slope. Additionally, previous studies have shown the numerical models applied in the estimation of the FOS; however, this study is focused on field and experimental data collection and sorting. As outlined in the research framework, the collected data is then deployed into intelligent prediction models to determine the FOS. This approach aims to facilitate easier design, construction, and performance monitoring of slope behavior during debris flow or earthquake-induced geohazard events.
Methodology
Governing equations, eulerian–lagrangian and the kinematics of flow on inclined surfaces.
The Eulerian–Lagrangian approach is a mathematical framework used to describe the behavior of fluid–solid mixtures 51 , which can include debris flows on inclined surfaces and slope stability failures. The coupled interface of this approach is presented in Fig. 1 . In this approach, the Eulerian framework describes the behavior of the fluid phase, while the Lagrangian framework describes the behavior of the solid phase 51 . For the specific case of debris flow on an inclined surface and slope stability failure, the equations can be quite complex and they depend on various factors, such as the properties of the debris, the slope geometry, and the flow conditions 51 . The governing equations for debris flow and slope stability failure are typically derived from fundamental principles of fluid mechanics and solid mechanics. These equations may include the Navier–Stokes equations for the fluid phase and constitutive models for the solid phase, as well as equations describing the interaction between the two phases 51 . In the Eulerian framework, the equations governing the behavior of the fluid phase (such as water and sediment mixture in debris flow) can include the continuity equation and the Navier–Stokes equations, which describe the conservation of mass and momentum for the fluid 51 . These equations can be adapted to account for the specific characteristics of debris flow, including non-Newtonian behavior and solid particle interactions. In the Lagrangian framework, the equations governing the behavior of the solid phase, such as the soil and rock material in slope stability failure, can include constitutive models that describe the stress–strain relationship of the material.
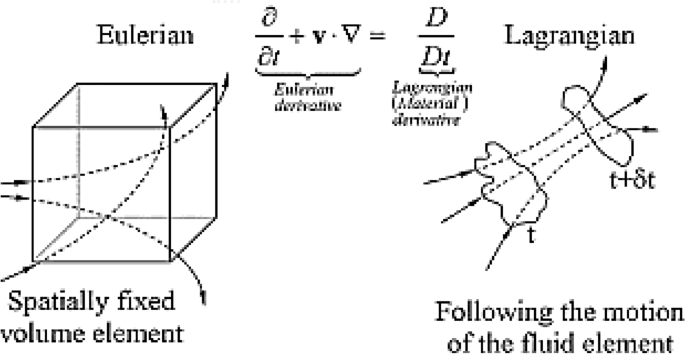
Eulerian–Lagrangian Interface.
These models can encompass factors such as strain softening, strain rate effects, and failure criteria. The interaction between the fluid and solid phases in the Eulerian–Lagrangian approach is typically described using additional terms that account for the exchange of momentum and mass between the phases 51 . These terms can include drag forces, buoyancy effects, and fluid-induced stresses on the solid phase. The specific form of the Eulerian–Lagrangian equations for debris flow on inclined surfaces and slope stability failure will depend on the details of the problem being studied, potentially requiring empirical data, numerical simulations, and experimental observations to validate and implement the equations effectively 16 . Due to the complexity of these equations, they are often solved using numerical methods, such as CFD and the DEM. In practice, researchers and engineers often use specialized software packages to simulate debris flow and slope stability failure, which implement the necessary equations and models within a computational framework to analyze and predict the behavior of these complex phenomena. The Eulerian mathematical equations for debris flow typically involve the conservation equations for mass, momentum, and energy, as well as constitutive relationships that describe the behavior of the debris material. Debris flow is a complex, multiphase flow phenomenon that involves the movement of a mixture of solid particles and fluid (usually water) down a slope 51 . The Eulerian approach describes the behavior of the mixture as it flows over the inclined surface. The continuity equation describes the conservation of mass for the debris flow mixture. In its Eulerian form, the continuity equation can be written as:
where ρ is the density of the mixture, φ is the volume fraction of the solid phase, t is time, v is the velocity vector of the mixture, and S represents any sources or sinks of the mixture 51 . The momentum equation describes the conservation of momentum for the debris flow mixture. In its Eulerian form, the momentum equation can be written as:
where v is the velocity vector of the mixture, τ is the stress tensor, g is the gravitational acceleration, and F represents any external forces acting on the mixture. The constitutive relationships describe the stress–strain behavior of the debris material 51 . These relationships can include models for the viscosity of the mixture, the drag forces between the solid particles and the fluid, and the interaction between the solid particles. Constitutive models for debris flow are often non-Newtonian and may involve empirical parameters based on experimental data. The energy equation describes the conservation of energy for the debris flow mixture. In its Eulerian form, the energy equation can be written as:
where E is the total energy per unit volume, k is the thermal conductivity, T is the temperature, and Q represents any heat sources or sinks. These equations, along with appropriate boundary conditions, form the basis for modeling and simulating debris flow using the Eulerian approach. However, it is important to note that the specific form of these equations may vary depending on the details of the problem being studied and the assumptions made in the modeling approach. Additionally, practical applications often involve numerical methods, such as CFD, to solve these equations and simulate the behavior of debris flow under different conditions 51 . When considering Lagrangian mathematical equations for debris flow on inclined surfaces, it is important to recognize that the Lagrangian approach focuses on tracking the motion and behavior of individual particles within the flow through space and time 51 . The equations of motion describe the trajectory and kinematics of individual particles within the debris flow 51 . These equations account for forces acting on the particles, such as gravity, drag forces, and inter-particle interactions. The equations can be written for each individual particle and may include terms representing the particle's mass, velocity, and acceleration. Constitutive relationships are used to describe the stress–strain behavior of individual particles and their interactions with the surrounding fluid. These models can encompass factors such as particle–particle interactions, particle–fluid interactions, and the rheological properties of the debris material 51 . Constitutive models for debris flow often consider the non-Newtonian behavior of the mixture and may involve empirical parameters based on experimental data. In the Lagrangian framework, it is important to account for erosion and deposition of particles as the debris flow moves over inclined surfaces. Equations describing erosion and deposition processes can be included to track changes in the particle distribution and the evolution of the flow 51 . The Lagrangian approach can also involve equations that describe the interaction of individual particles with the surrounding environment, including the boundary conditions of the inclined surface and any obstacles or structures in the flow path. This approach accounts for the interaction between the solid particles and the fluid phase within the debris flow 51 . Equations can be included to represent the drag forces, buoyancy effects, and fluid-induced stresses acting on the individual particles. The Lagrangian approach for debris flow involves tracking a large number of individual particles, which can be computationally intensive. Numerical simulations using DEMs are often employed to solve the Lagrangian equations and simulate the behavior of debris flow on inclined surfaces. In practice, researchers and engineers use specialized software and numerical methods to simulate debris flow behavior in the Lagrangian framework, taking into account the complexities of particle–fluid interactions, erosion and deposition processes, and the influence of slope geometry on flow dynamics 51 .
The kinematics of flow on inclined surfaces refers to the study of the motion and deformation of a fluid as it moves over an inclined plane or surface. Understanding the kinematics of flow on inclined surfaces is important in various fields, including fluid mechanics, civil engineering, and geology.
Here are some key concepts related to the kinematics of flow on inclined surfaces: When a fluid flows over an inclined surface, the behavior of the free surface, or the boundary between the fluid and the surrounding air or other media, is of particular interest 51 . The shape of the free surface and how it deforms as the fluid flows downhill can provide important insights into the flow behavior 15 . The kinematics of flow on inclined surfaces involves studying how the flow velocity and depth vary along the inclined plane. The flow profiles can be influenced by factors, including gravity, surface roughness, and the viscosity of the fluid. The Reynolds number, which is a dimensionless quantity that characterizes the flow regime, can be used to understand the transition from laminar to turbulent flow on inclined surfaces. This transition affects the flow kinematics and the development of flow structures 51 . The shear stress exerted by the flow on the inclined surface and the resulting bed shear stress are important parameters that influence the kinematics of the flow. They can affect sediment transport, erosional processes, and the development of boundary layers. Flow separation occurs when the fluid detaches from the inclined surface, leading to distinct flow patterns. Reattachment refers to the subsequent rejoining of the separated flow with the surface. Understanding these phenomena is crucial for predicting the flow kinematics and associated forces. As the fluid moves down an inclined surface, it often experiences changes in velocity, which can result in acceleration or deceleration of the flow. Understanding the spatial and temporal variations in flow velocity is essential for analyzing the kinematics of the flow. The kinematics of flow on inclined surfaces also involves the study of energy dissipation processes, including the conversion of potential energy to kinetic energy and the associated losses due to friction and turbulence. Studying the kinematics of flow on inclined surfaces often involves experimental measurements, theoretical modeling, and numerical simulations 51 . Researchers and engineers use various techniques, such as flow visualization, particle image velocimetry (PIV), and CFD, to analyze the kinematic behavior of fluid flow on inclined surfaces and to gain insights into the associated transport and geomorphic processes. The mathematical description of flow kinematics on an inclined surface typically involves the characterization of the flow velocity, depth, and other flow-related parameters as a function of position and time. For steady or unsteady flow on an inclined surface, the following equations and concepts are commonly used to describe the flow kinematics. The velocity field of the flow on an inclined surface can be described using components in the direction parallel to the surface and perpendicular to the surface. For example, in Cartesian coordinates, the velocity components can be denoted as u(x, y, z) in the x-direction, v(x, y, z) in the y-direction, and w(x, y, z) in the z-direction. The continuity equation expresses the conservation of mass within the flow and relates the variations in flow velocity to changes in flow depth. In 1D form, the continuity equation for steady, uniform flow on an inclined surface can be expressed as:
where A is the cross-sectional area of flow, V is the average velocity of the flow, and Q is the flow discharge. The flow depth, which represents the vertical distance from the free surface to the bed of the channel, is an essential parameter in the kinematic description of flow 51 . For uniform flow on an inclined surface, the flow depth can be related to the flow velocity using specific energy concepts. Manning's equation is commonly used to relate flow velocity to flow depth and channel slope in open channel flow, including flow on inclined surfaces 51 . It is an empirical equation often used in open-channel hydraulics to estimate flow velocity using the flow depth, channel roughness, and slope. The momentum equations describe the conservation of momentum within the flow and account for forces acting on the flow, including gravity, pressure gradients, and viscous forces 51 . The momentum equations can be expressed using the Navier–Stokes equations for viscous flows or simplified forms of inviscid flows. For viscous flow on an inclined surface, boundary layer theory can be used to analyze the velocity profiles and the development of boundary layers near the surface. This provides insights into the distribution of flow velocity and shear stress close to the boundary 51 . The energy equations describe the conservation of energy within the flow and relate the flow velocity and depth to the energy state of the flow. In open channel flow, the energy equations can be expressed in terms of specific energy, relating it to flow depth and velocity. These mathematical equations and concepts provide a framework for the analysis of flow kinematics on inclined surfaces. The specific equations used will depend on the nature of the flow (e.g., steady or unsteady, uniform or non-uniform) and the assumptions made regarding flow behavior. In practice, engineers and researchers often apply these equations in conjunction with experimental data and numerical simulations to analyze and predict the kinematic behavior of flow on inclined surfaces.
Viscoplastic-viscoelastic models (bingham model, casson model, and power law)
The study of debris flow down a slope involves complex material behavior, which can be approximated using viscoplastic-viscoelastic models. Debris flows are rapid mass movements of a combination of water, sediment, and debris down a slope, and they exhibit both solid-like and fluid-like behavior 51 . A viscoplastic-viscoelastic model aims to capture several aspects of debris flow behavior. Debris flows often exhibit solid-like behavior under low strain rates, where the material behaves like a viscoplastic solid. This means that the material deforms and flows plastically under stress, exhibiting a yield stress beyond which it begins to flow. At higher strain rates, debris flows can display fluid-like behavior with viscoelastic properties. This means that the material exhibits a combination of viscous (fluid-like) and elastic (solid-like) responses to applied stress 16 . Viscoelasticity accounts for the time-dependent deformation and stress relaxation observed in the flow. To model this complex behavior, a viscoplastic-viscoelastic model for debris flow would likely involve a combination of constitutive equations to represent both the solid-like and fluid-like behavior of the material. One possible approach is to use a combination of a viscoplastic model, such as a Bingham or Herschel-Bulkley model, to capture the material's yield stress and plastic behavior, along with a viscoelastic model, such as a Maxwell or Kelvin-Voigt model, to capture the time-dependent deformation and stress relaxation 51 . Implementing such a model would involve determining the material parameters through laboratory testing and field observations, as well as solving the governing equations of motion for the debris flow, taking into account the complex interactions between the solid and fluid components of the flow. It is important to note that modeling debris flow behavior is a highly complex and multidisciplinary task, involving aspects of fluid mechanics, solid mechanics, and rheology, among others. Therefore, the specific details of the viscoplastic–viscoelastic model would depend on the particular characteristics and behavior of the debris flow being studied. When studying debris flow down a slope, various rheological models can be used to describe the flow behavior of the mixture of water, sediment, and debris 51 . It is important to understand the Bingham, Casson, and power law models, along with how they can be applied to debris flow. The Bingham model is a simple viscoplastic model that describes the behavior of materials that have a yield stress and exhibit viscous behavior once the yield stress is exceeded. In the context of debris flow, the Bingham model can be used to represent the behavior of the flow when it behaves like a solid, with no deformation occurring until a critical stress, known as the yield stress, is reached. Once the yield stress is exceeded, the material flows like a viscous fluid 51 . The Bingham model can be expressed mathematically using Eqs. ( 5 )–( 7 ). The Bingham model is characterized by a yield stress (τ_y), which represents the minimum stress required to initiate flow 51 . This is known as the yield criterion, which can be expressed as:
where τ is the total stress tensor. Viscous flow occurs when the yield stress is exceeded, with the material behaving like a Newtonian fluid with a dynamic viscosity (μ). The relationship between the shear stress (τ) and the shear rate (du/dy) is given by:
Combining these equations, the Bingham model can be summarized as follows:
In the context of debris flow down a slope, these equations can be applied to describe the behavior of the flow when it behaves like a solid (below the yield stress) and when it behaves like a viscous fluid (above the yield stress). It is important to note that in the case of debris flow, the Bingham model may need to be extended or combined with other models to more accurately capture the complex behavior of the flow, especially considering the multiphase nature of debris flow involving water, sediment, and debris 2 , 5 , 9 , 51 . Additionally, specific boundary conditions and rheological parameters need to be considered and may require calibration based on experimental and field data. The Casson model is another rheological model that accounts for the yield stress of a fluid, while also considering the square root of the shear rate in the relationship between shear stress and shear rate. It is useful for describing the behavior of non-Newtonian fluids with a yield stress, and it can be applied to debris flow to capture the transition from solid-like to fluid-like behavior 7 . In the context of debris flow down a slope, the Casson model can be used to capture this transition as the yield stress is exceeded 16 . The Casson model can be expressed mathematically using the following Eqs. ( 8 ) and ( 9 ). Similar to the Bingham model, the Casson model includes a yield stress (τ y ), which represents the minimum stress required to initiate flow. The yield criterion can be expressed as:
where τ is the total stress tensor and K is a parameter related to the plastic viscosity of the fluid. Viscous flow occurs once the yield stress is exceeded, with the material behaving like a Casson fluid. The relationship between the shear stress (τ) and the shear rate (du/dy) is given by 51 :
In the context of debris flow down a slope, these equations can be applied to describe the behavior of the flow when it behaves like a solid (below the yield stress) and when it behaves like a fluid (above the yield stress) 51 . It is important to note that the Casson model provides a more complex description of non-Newtonian fluids compared to the Bingham model, and it may capture more nuanced rheological behavior exhibited by debris flow. However, as with any rheological model, the specific parameters and boundary conditions for the Casson model need to be carefully considered and may require calibration based on experimental and field data to accurately represent the behavior of debris flow 16 . The power law model, also known as the Ostwald–de Waele model, describes a non-Newtonian fluid's behavior where the shear stress is proportional to the power of the shear rate. This model is commonly used to describe the behavior of fluids with shear-thinning or shear-thickening properties. In the context of debris flow, the power law model can be used to capture the non-Newtonian behavior of the flow, particularly if the flow exhibits shear-thinning or shear-thickening characteristics 51 . The power law model can be expressed mathematically using Eq. ( 10 ). The viscous flow relationship describes the relationship between shear stress (τ) and shear rate (du/dy) for a non-Newtonian fluid and is expressed as follows:
where τ is the shear stress; du/dy is the shear rate; K is the consistency index, which represents the fluid's resistance to flow; and n is the flow behavior index, which characterizes the degree of shear-thinning or shear-thickening behavior. For n < 1, the fluid exhibits shear-thinning behavior, and for n > 1, the fluid exhibits shear-thickening behavior 51 . In the context of debris flow down a slope, these equations can be applied to describe the non-Newtonian behavior of the flow, taking into account the varying shear rates and stress conditions experienced during flow. It is important to note that the power law model provides a simplified but versatile representation of the rheological behavior of non-Newtonian fluids. However, when applying the power law model to debris flow, it is essential to consider the specific characteristics of the flow, such as the mixture of water, sediment, and debris, and the complex interactions between the different phases 51 . As with any rheological model, calibration and validation based on experimental and field data are crucial for accurately representing the behavior of debris flow. When applying these models to debris flow down a slope, it is important to recognize that debris flow is a complex, multiphase flow involving interactions between water, sediment, and debris 5 . Therefore, the choice of rheological model should be based on the specific characteristics of the debris flow being studied, as well as the available data and observations 1 . It is also worth noting that these models provide a simplified representation of the complex behavior of debris flow, and more sophisticated models, such as viscoelastic-viscoplastic models, may be necessary to capture the full range of behaviors observed in debris flows. Additionally, field and laboratory data are crucial for calibrating and validating any rheological model used to describe debris flow behavior 37 . The Navier–Stokes equations are a set of partial differential equations that describe the motion of fluid substances. When applied to debris flow down a slope, the Navier–Stokes equations can be used to model the conservation of momentum and mass for the generalized flow of the mixture of water, sediment, and debris 51 . The Navier–Stokes equations are typically written in vector form to describe the conservation of momentum and mass in three dimensions. The conservation of momentum for the generalized flow model of debris flow down a slope is governed by the Navier–Stokes equations, which can be written in vector form as follows:
where \(\frac{{D_{u} }}{{D_{t} }}\) represents the velocity vector of the debris flow; t is time; \(\rho\) is the density of the mixture; \(\nabla\) is the deviatoric stress tensor, which accounts for the shear stress within the flow; and \(\otimes\) denotes the dot product. The terms on the right-hand side of the equation represent, from left to right, the pressure gradient, the viscous effects (stress), and the gravitational force 51 . The conservation of mass is described by the continuity equation. The continuity equation represents the conservation of mass within the flow, stating that the rate of change of mass within a control volume is equal to the net flow of mass into or out of the control volume 51 . When modeling debris flows down a slope using the Navier–Stokes equations, it is important to consider the complex nature of the flow, including the interactions between water, sediment, and debris, as well as the influence of the slope geometry, boundary conditions, and other relevant factors. Additionally, the rheological behavior of the debris flow, such as its viscosity and yield stress, can be incorporated into the stress terms in the momentum equation to model the non-Newtonian behavior of the flow.
Theory of the model techniques
Extreme learning machines (elms).
Extreme learning machines (ELMs), depicted in Fig. 2 , are machine learning algorithms that belong to the family of neural networks. They were introduced by Guang-Bin Huang, Qin-Yu Zhu, and Chee-Kheong Siew in 2006. ELMs are known for their simple and efficient training process, particularly when compared to traditional neural networks, such as multi-layer perceptrons (MLPs). The key idea behind ELMs is to randomly initialize the input weights and analytically determine the output weights, rather than using iterative techniques like backpropagation. This approach allows ELMs to achieve fast training times, making them particularly suitable for large-scale learning problems 52 . ELMs have been applied to various tasks, including classification, regression, feature learning, and clustering. They have found use in fields such as pattern recognition, image and signal processing, and bioinformatics. Despite their advantages, it is worth noting that ELMs may not always outperform traditional neural networks, especially on complex tasks that require fine-tuning and iterative learning. Additionally, ELMs’ random weight initialization can lead to some variability in performance, which may require careful consideration when using the algorithm in practical applications 53 . The theoretical framework of ELMs is based on the concept of single-hidden-layer feedforward neural networks. There are several key components of the theoretical framework. Random hidden layer feature mapping: ELMs start by randomly initializing the input weights and the biases of the hidden neurons. These random weights are typically drawn from a uniform or Gaussian distribution 54 . The random feature mapping of the input data to the hidden layer means ELMs can avoid the iterative training process used in traditional neural networks. Analytical output weight calculation: After random feature mapping, ELMs analytically calculate the output weights by solving a system of linear equations. This step does not involve an iterative optimization process, which contributes to the computational efficiency of ELMs. Universal approximation theorem: The theoretical foundation of ELMs is grounded in the universal approximation theorem, which states that a single-hidden-layer feedforward neural network with a sufficiently large number of hidden neurons can approximate any continuous function to arbitrary accuracy 55 . ELMs leverage this theorem to achieve high learning capacity and generalization performance. Regularization and generalization: ELMs’ theoretical framework includes considerations for regularization techniques to prevent overfitting and improve generalization performance. Common regularization methods used in ELMs include Tikhonov regularization (also known as ridge regression) and pruning of irrelevant hidden neurons. Computational efficiency: ELMs’ theoretical framework emphasizes computational efficiency by reducing the training time and computational cost associated with traditional iterative learning algorithms. This efficiency is achieved through the combination of random feature mapping and analytical output weight calculations. Overall, the theoretical framework of ELMs is characterized by its unique approach to training single-hidden-layer feedforward neural networks, leveraging randomization and analytical solutions to achieve fast learning and good generalization performance. Basic notations are required to formulate the prediction output of ELMs. Each input feature vector is denoted as \(x_{i} \epsilon R^{d}\) , where i = 1, 2, …, N number of features, with N being the number of samples or data points. The corresponding output for each input is denoted as \(y_{i}\) . The model representation considers a single-hidden-layer feedforward neural network with L hidden nodes (neurons). The input–output relationship of the network can be represented as:
where \(w_{j}\) is the weight vector for the j-th hidden node, \(b_{j}\) is the bias term for the j-th hidden node, \(g\left( . \right)\) is the activation function applied element-wise, and \(\beta_{j}\) is the weight associated with the output of the j-th hidden node. To initialize training, weights ( \(w_{j}\) ) and biases ( \(b_{j}\) ) are randomly assigned for each hidden node and an activation function, \(g\left( . \right)\) , is chosen. Then, the output of the hidden layer for all input samples is computed, thus:
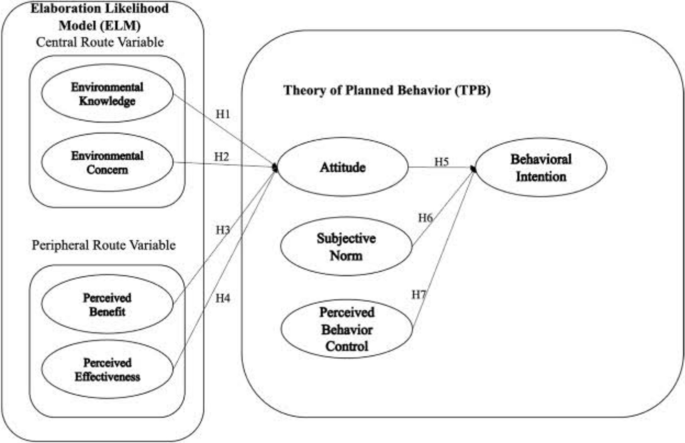
ELM framework.
To compute the output weight, the output weight vector ( \(\beta\) ) is solved using the least squares method:
where Y is the matrix of the target values. Once the output weights are computed, the model can predict new outputs using the learned parameters.
Least squares support vector machine (LSSVM)
LSSVM stands for least squares support vector machine, which is a supervised learning algorithm used for regression, classification, and time-series prediction tasks. LSSVM, the framework of which is illustrated in Fig. 3 , is a modification of the traditional support vector machine (SVM) algorithm, and it was introduced by Suykens and Vandewalle in the late 1990s. The LSSVM is formulated as a set of linear equations, whereas the traditional SVM is formulated as a convex optimization problem 53 . This allows the LSSVM to be solved using linear algebra techniques, which can be computationally efficient, especially for large datasets. Similar to the SVM, the LSSVM can benefit from the kernel trick, which allows it to implicitly map input data into a higher-dimensional space, enabling the algorithm to handle non-linear relationships between input features and the target variable. The LSSVM incorporates a regularization parameter that helps to control the trade-off between fitting the training data and maintaining a smooth decision boundary or regression function 55 . Regularization is important for preventing overfitting. The LSSVM is often expressed in a dual formulation, similar to SVM. This formulation allows the algorithm to operate in a high-dimensional feature space without explicitly computing the transformed feature vectors. The LSSVM transforms the original optimization problem into a system of linear equations, which can be efficiently solved using matrix methods, such as the Moore–Penrose pseudoinverse or other numerical techniques. The LSSVM has been applied to various real-world problems, including regression tasks in finance, time-series prediction in engineering, and classification tasks in bioinformatics 52 . Its ability to handle non-linear relationships and its computational efficiency makes it a popular choice for many machine learning applications. Overall, the LSSVM is a versatile algorithm that combines the principles of support vector machines with the computational advantages of solving linear equations, making it a valuable tool for a wide range of supervised learning tasks. The theoretical framework of the LSSVM is grounded in the principles of statistical learning theory and convex optimization. It is useful to understand the key components of the theoretical framework of the LSSVM. Formulation as a linear system: The LSSVM is formulated as a set of linear equations, in contrast to the quadratic programming problem formulation of traditional SVM. This linear equation formulation allows LSSVM to be solved using linear algebra techniques, such as the computation of the Moore–Penrose pseudoinverse, which can lead to computational efficiency, especially for large datasets 52 . Kernel trick: Similar to the traditional SVM, the LSSVM can benefit from the kernel trick, which enables it to implicitly map the input data into a higher-dimensional feature space. This allows the LSSVM to capture non-linear relationships between input features and the target variable without explicitly transforming the input data. Regularization: The LSSVM incorporates a regularization parameter (often denoted as \(\gamma \)) that controls the trade-off between fitting the training data and controlling the complexity of the model 55 . Regularization is essential for preventing overfitting and improving the generalization performance of the model. Dual Formulation: The LSSVM is often expressed in a dual formulation, similar to the traditional SVM. The dual formulation allows the LSSVM to operate in a high-dimensional feature space without explicitly computing the transformed feature vectors, leading to computational advantages. Convex optimization: The theoretical framework of the LSSVM involves solving a convex optimization problem, which ensures that the training algorithm converges to the global minimum and guarantees the optimality of the solution. Statistical learning theory: The LSSVM is founded on the principles of statistical learning theory, which provides a theoretical framework for understanding the generalization performance of learning algorithms and the trade-offs between bias and variance in model fitting 54 . Overall, the theoretical framework of the LSSVM integrates principles from convex optimization, statistical learning theory, and kernel methods. By leveraging these principles, the LSSVM aims to achieve a balance between model complexity and data fitting while providing computational efficiency and the ability to capture non-linear patterns in the data. Basic notations are required to formulate the output for the LSSVM prediction. Each input feature vector is denoted as \(x_{i} \epsilon R^{d}\) , where i = 1, 2, …, N number of features, with N being the number of training samples. The corresponding output for each input is denoted as \(y_{i} \epsilon \left\{ { - 1, 1} \right\}\) for binary classifications. The standard SVM aims to find a hyperplane characterized by a weight vector (w) and a bias term (b) that separates the data into two classes with a maximal margin. The optimization problem is given by:
where C is a regularization parameter that controls the trade-off between achieving a small margin and allowing some training points to be misclassified. The LSSVM replaces the hinge loss with a least squares loss, resulting in the following optimization problem:
LSSVM framework.
Subject to the constraints:
where \(e_{i}\) represents the slack variables, allowing for soft-margin classification, \(\gamma\) is a regularization parameter controlling the trade-off between fitting the data well and keeping the model simple. The constraints ensure that each data point lies on or inside the margin. In the dual form, the Lagrangian for the LSSVM dual problem is:
where \(\alpha_{i}\) are the Lagrange multipliers, and \(K\left( {x_{i} x_{j} } \right)\) is the kernel function, capturing the inner product of the input vectors. Once the Lagrange multipliers ( \(\alpha_{i}\) ) are obtained, the decision function for a new input, x is given by:
where b is determined during training.
Adaptive neuro-fuzzy inference system (ANFIS)
ANFIS stands for adaptive neuro-fuzzy inference system, the framework of which is shown in Fig. 4 . It is a hybrid intelligent system that combines the adaptive capabilities of neural networks with the human-like reasoning of fuzzy logic. ANFIS models are particularly well-suited for tasks that involve complex, non-linear relationships and uncertain or imprecise information 51 . Fuzzy inference system (FIS): The ANFIS is based on the principles of fuzzy logic, which allows for the representation and processing of uncertain or vague information. Fuzzy logic uses linguistic variables, fuzzy sets, and fuzzy rules to capture human expert knowledge and reasoning. These fuzzy rules are often expressed in the form of ‘‘if–then’’ statements. Neural network learning: The ANFIS incorporates the learning capabilities of neural networks to adapt and optimize its parameters based on input–output training data. This learning process enables the ANFIS to model complex non-linear relationships between input variables and the output, similar to traditional neural network models 52 . Hybrid learning algorithm: The learning algorithm used in the ANFIS is a hybrid of gradient descent and least squares estimation. This hybrid approach allows the ANFIS to optimize its parameters by leveraging both the error backpropagation commonly used in neural networks and the least squares method used in statistical modeling. Membership function adaptation: The ANFIS includes a mechanism for adapting the membership functions and fuzzy rules based on the input data 55 . This adaptation process allows the ANFIS to capture the nuances and variations in the input–output relationships, leading to improved model accuracy. Rule-based reasoning: The ANFIS employs rule-based reasoning to combine the fuzzy inference system and neural network learning. This integration enables the ANFIS to benefit from the interpretability and knowledge representation capabilities of fuzzy logic while leveraging the learning and generalization capabilities of neural networks. Applications: The ANFIS has been applied to various real-world problems in areas such as control systems, pattern recognition, time-series prediction, and decision support 51 . Its ability to handle complex, non-linear relationships and uncertain data makes it a valuable tool for a wide range of applications. In summary, the theoretical framework of the ANFIS is rooted in the integration of fuzzy logic and neural network learning, allowing it to effectively model complex systems and uncertain information by combining the strengths of both paradigms. The theoretical framework of the ANFIS can be understood through several key components. Fuzzy logic: The ANFIS is built upon the principles of fuzzy logic, which provides a framework for representing and processing uncertain or vague information. Fuzzy logic allows for the modeling of linguistic variables, fuzzy sets, and fuzzy rules, which capture the imprecision and uncertainty present in many real-world problems 52 . FIS: The ANFIS incorporates the structure of a FIS, which consists of linguistic variables, fuzzy sets, membership functions, and fuzzy rules. These elements are used to represent expert knowledge and reasoning in a human-interpretable form. Neural network learning: The ANFIS integrates the learning capabilities of neural networks to adapt and optimize its parameters based on training data. The use of neural network learning allows the ANFIS to model complex, non-linear relationships between input variables and the output, similar to traditional neural network models. Hybrid learning algorithm: The ANFIS uses a hybrid learning algorithm that combines the principles of gradient descent and least squares estimation 54 . This hybrid approach enables the ANFIS to optimize its parameters by leveraging both the error backpropagation commonly used in neural networks and the least squares method used in statistical modeling. Membership function adaptation: The ANFIS includes mechanisms for adapting the membership functions and fuzzy rules based on the input data. This adaptation process allows the ANFIS to capture the nuances and variations in the input–output relationships, leading to improved model accuracy. Rule-based reasoning: The ANFIS employs rule-based reasoning to combine the FIS and neural network learning. This integration enables the ANFIS to benefit from the interpretability and knowledge representation capabilities of fuzzy logic while leveraging the learning and generalization capabilities of neural networks. Parameter optimization: The ANFIS aims to optimize its parameters, including the parameters of the membership functions and the rule consequent parameters, to minimize the difference between the actual and predicted outputs. Applications: The ANFIS has been applied to various real-world problems in areas such as control systems, pattern recognition, time-series prediction, and decision support. Its ability to handle complex, non-linear relationships and uncertain data makes it a valuable tool for a wide range of applications. In summary, the theoretical framework of the ANFIS is rooted in the integration of fuzzy logic and neural network learning, allowing it to effectively model complex systems and uncertain information by combining the strengths of both paradigms. In the formulation of the output for the ANFIS prediction of engineering problems, the following basic notations are used: Each input feature vector is denoted as xi = (x i 1, x i 2,…, x i m), where i = 1, 2, …, N, with N being the number of training samples and m is the number of input variables. The corresponding output or target for each input is denoted as y i and the f(x) represents the overall ANFIS output for a given input x. Hence, the ANFIS output f(x) can be expressed as a weighted sum of the rule consequents:
where J is the number of fuzzy rules, w j is the weight associated with the j-th rule, and y i is the output of the j-th rule.
ANFIS framework.
Eagle optimization (EO)
The eagle optimization (EO) algorithm (see framework in Fig. 5 ) is a metaheuristic optimization algorithm inspired by the hunting behavior of eagles. Like other metaheuristic algorithms, the EO algorithm is designed to solve optimization problems by iteratively improving solutions to find the best possible solution within a search space 55 . It is useful to have an understanding of the EO metaheuristic algorithm. Inspiration from eagle behavior: The EO algorithm is based on the hunting behavior of eagles in nature. Eagles are known for their keen vision and hunting strategies, which involve searching for prey and making decisions about the best approach to capture it. Population-based approach: Similar to other metaheuristic algorithms, the EO algorithm operates using a population of candidate solutions 53 . These candidate solutions are represented as individuals within the population, and the algorithm iteratively improves these solutions to find the optimal or near-optimal solution to the given optimization problem. Exploration and exploitation: The EO algorithm balances exploration of the search space (similar to the hunting behavior of eagles searching for prey) and exploitation of promising regions to refine and improve solutions. Solution representation: Candidate solutions in the EO algorithm are typically represented in a manner suitable for the specific optimization problem being solved. This representation could be binary, real-valued, or discrete, depending on the problem domain. Objective function evaluation: The fitness or objective function evaluation is an essential component of the EO algorithm. The objective function quantifies the quality of a solution within the search space, which is used to guide the search towards better solutions. Search and optimization process: The EO algorithm iteratively performs search and optimization by simulating the movement of eagles hunting for prey 55 . The algorithm uses various operators, such as crossover, mutation, and selection, to explore and exploit the search space. Parameter settings: Like most metaheuristic algorithms, the EO algorithm involves setting parameters that control its behavior, such as population size, mutation rate, crossover rate, and other algorithm-specific parameters. Convergence and termination: The algorithm continues to iterate until a termination criterion is met, such as reaching a maximum number of iterations, achieving a satisfactory solution, or other stopping criteria. Metaheuristic algorithms like the EO algorithm are widely used for solving complex optimization problems in various domains, including engineering, operations research, and machine learning. They provide a flexible and efficient approach for finding near-optimal solutions in situations where traditional exact optimization methods may be impractical due to the complexity of the problem or the computational cost of exact solutions.

EO framework.
Particle swarm optimization (PSO)
The framework of particle swarm optimization (PSO), as illustrated in Fig. 6 , is a population-based metaheuristic optimization algorithm inspired by the social behavior of bird flocking or fish schooling. It was originally proposed by Kennedy and Eberhart in 1995 55 . PSO is commonly used to solve optimization problems, including continuous and discrete optimization, as well as in training the parameters of machine learning models. Particle representation: In PSO, a potential solution to an optimization problem is represented as a ‘‘particle.’’ Each particle has a position and a velocity in the search space 55 . These positions and velocities are updated iteratively as the algorithm searches for the optimal solution. Fitness evaluation: The quality of each particle's position is evaluated using an objective function, which measures how well the particle's position performs in solving the optimization problem. This objective function guides the search for the optimal solution 55 . Swarm behavior: PSO is based on the concept of swarm intelligence, where the particles collaborate and communicate with each other to explore the search space. The particles adjust their positions and velocities based on their own experience and the experiences of their neighboring particles. Velocity and position update: The velocity and position of each particle are updated using formulas that take into account the particle's previous velocity, its distance to the best solution it has encountered (individual best), and the distance to the best solution found by any particle in the swarm (global best) 55 . Exploration and exploitation: PSO balances exploration and exploitation of the search space. Initially, particles explore the search space widely to discover promising regions. As the algorithm progresses, they exploit the best regions found so far to converge towards the optimal solution. Convergence and stopping criteria: PSO typically includes stopping criteria to halt the search when certain conditions are met, such as reaching a maximum number of iterations or achieving a satisfactory level of solution quality 55 . Applications in machine learning: PSO is used in machine learning for tasks such as feature selection, parameter tuning in neural networks and other models, as well as in training the weights of neural networks and other optimization problems related to machine learning. In summary, the theoretical framework of PSO is based on the concept of swarm intelligence and social behavior, where particles in a population collectively explore the search space to find optimal solutions. PSO has been widely applied in various fields, including machine learning, due to its ability to efficiently solve complex optimization problems. PSO is primarily an optimization algorithm rather than a learning algorithm in the traditional sense. However, it possesses certain learning capabilities that enable it to adapt and improve its search behavior as it iteratively explores the solution space 53 . Adaptation of particle velocity and position: PSO's learning capability is manifested in the way particles adapt their velocities and positions based on their own experience and the experiences of their neighboring particles 53 . Through this process, particles learn to navigate the solution space in search of better solutions. Social learning: PSO particles learn from the collective knowledge of the swarm. They are influenced by the best solutions found by other particles (global best) and the best solutions they have individually encountered (individual best) 55 . This social learning aspect allows for the sharing and propagation of good solutions within the swarm. Exploration and exploitation: PSO dynamically balances exploration and exploitation as the algorithm progresses. Initially, particles explore the solution space widely to discover promising regions. As the algorithm continues, they exploit the best regions found so far to converge towards the optimal solution. This adaptive behavior can be considered a form of learning from the search process. Convergence behavior: Through its iterative process, PSO exhibits convergence behavior, where the swarm gradually focuses its search around promising regions of the solution space. This convergence can be seen as a form of learning from the algorithm's experience, as it adjusts its behavior based on the information gathered during the search. While PSO does exhibit learning-like behaviors in terms of adaptation, social information sharing, and convergence, it is important to note that its learning capabilities are fundamentally different from those of supervised learning algorithms used in traditional machine learning. PSO's learning is focused on adapting the behavior of the swarm to efficiently explore and exploit the solution space in the context of optimization problems, rather than on generalizing patterns from data or making predictions.
PSO framework.
Harris Hawks optimization (HHO)
The framework of Harris hawks optimization (HHO), as presented in Fig. 7 , is a metaheuristic algorithm inspired by the hunting behavior of Harris hawks 52 . Metaheuristic algorithms are optimization algorithms that can be used to find solutions to difficult optimization problems, particularly in the field of machine learning 52 . In the context of machine learning, metaheuristic algorithms like HHO can be used for various tasks, such as feature selection, hyperparameter tuning, and even optimizing the structure of neural networks 52 . These algorithms are particularly useful when the search space is large and complex, where traditional optimization methods might struggle to find good solutions in a reasonable amount of time. When applying HHO or similar metaheuristic algorithms to machine learning problems, it is important to carefully define the optimization problem and the constraints, as well as to properly tune the algorithm's parameters to ensure good performance 52 . Overall, metaheuristic algorithms like HHO can be valuable tools in the machine learning practitioner's toolbox, particularly for challenging optimization tasks where traditional methods may not be effective. The learning capabilities of the HHO algorithm, as with other metaheuristic algorithms, are based on its ability to efficiently explore and exploit the search space to find near-optimal solutions to complex optimization problems 52 . It is useful to understand some of the key learning capabilities of HHO. Exploration and exploitation: HHO is designed to balance exploration and exploitation of the search space. During the early stages of the optimization process, HHO explores the search space to discover diverse solutions. As the process continues, it shifts towards exploiting the most promising regions of the search space to refine and improve the solutions 52 . Adaptive search: HHO is capable of adapting its search behavior based on the characteristics of the problem being optimized. This adaptability allows it to efficiently navigate different types of search spaces, including high-dimensional, non-convex, and multimodal spaces. Global and local search: HHO is able to perform both global and local searches. It can efficiently explore the entire search space to find the global optimum, while also focusing on local regions to fine-tune solutions. Convergence and diversification: HHO aims to converge to high-quality solutions while maintaining diversity in the population of candidate solutions. This balance helps prevent premature convergence to suboptimal solutions and encourages continued exploration of the search space 52 . Robustness: HHO exhibits robustness in handling noisy or uncertain objective functions. It is able to adapt to noisy environments and continue to improve solutions in the presence of uncertainty. Scalability: HHO can scale to handle large-scale optimization problems, making it suitable for real-world applications with complex, high-dimensional search spaces 52 . Overall, the learning capabilities of HHO make it well-suited for tackling challenging optimization problems in various domains, including machine learning, engineering, and operations research. When applied to machine learning tasks, HHO can be used for feature selection, hyperparameter optimization, model tuning, and other optimization challenges encountered in the development and deployment of machine learning systems.
HHO framework 52 .
Genetic algorithms (GA)
Genetic algorithms (GAs), the framework of which is presented in Fig. 8 , are a class of metaheuristic algorithms that are inspired by the process of natural selection and genetic evolution 54 . They are used to find approximate solutions to optimization and search problems. It is important to understand the key aspects and capabilities of these algorithms. Representation of solutions: In GAs, potential solutions to the optimization problem are represented as individuals in a population 54 . These individuals are typically encoded as strings of symbols, such as binary strings, and are often referred to as chromosomes. Selection: GAs use a selection process to choose individuals from the population for reproduction, typically based on their fitness (i.e., how well they solve the given problem). This process is analogous to the principle of ‘‘survival of the fittest’’ in natural selection 54 . Crossover: During reproduction, GAs perform crossover or recombination, where pairs of selected individuals exchange genetic information to create new offspring. This is often implemented by swapping or mixing parts of the chromosomes of the selected individuals. Mutation: GAs include a mutation step, which introduces random changes in the genetic information of the offspring 54 . Mutation helps to maintain genetic diversity in the population and avoid premature convergence to suboptimal solutions. Fitness evaluation: The fitness of individuals in the population is evaluated based on a predefined objective or fitness function. This function quantifies how well a particular solution addresses the optimization problem. Population dynamics: GAs maintain a population of solutions over multiple generations. Through the processes of selection, crossover, and mutation, the population evolves over time, with the hope that better solutions emerge in later generations 54 . Convergence: GAs aim to converge toward better solutions over successive generations 55 . They are designed to balance the exploration of the search space with the exploitation of promising regions to find high-quality solutions. Application in machine learning: GAs have been applied in various areas of machine learning, including feature selection, hyperparameter optimization, neural network architecture search, and data preprocessing. They can be particularly useful in problems where the search space is large and complex 55 . GAs are known for their versatility and have been successfully applied to a wide range of optimization problems in different domains 54 . When appropriately applied, they can be effective in finding near-optimal solutions to challenging optimization problems. The learning capabilities of GAs stem from their ability to efficiently explore and exploit the search space to find near-optimal solutions to complex optimization problems. It is important to understand the key aspects and capabilities of these algorithms. Exploration and exploitation: GAs are designed to balance exploration and exploitation of the search space. During the early stages of the optimization process, GAs explore the search space to discover diverse solutions 54 . As the process progresses, they shift towards exploiting the most promising regions of the search space to refine and improve the solutions. Adaptation to problem characteristics: GAs exhibit adaptability, allowing them to efficiently navigate different types of search spaces, including high-dimensional, non-convex, and multimodal spaces 54 . This adaptability enables GAs to effectively address a wide variety of optimization problems. Global and local search: GAs are capable of performing both global and local searches. They can efficiently explore the entire search space to find the global optimum, while also focusing on local regions to fine-tune solutions. Convergence and diversification: GAs aim to converge to high-quality solutions while maintaining diversity in the population of candidate solutions 54 . This balance helps prevent premature convergence to suboptimal solutions and encourages continued exploration of the search space. Robustness: GAs are robust in handling noisy or uncertain objective functions. They are able to adapt to noisy environments and continue to improve solutions in the presence of uncertainty. Scalability: GAs can scale to handle large-scale optimization problems, making them suitable for real-world applications with complex, high-dimensional search spaces 55 . Parallelization: GAs can be parallelized to explore the search space more efficiently, especially when dealing with computationally intensive problems. This parallelization capability can lead to improved learning and convergence speed. Versatility: GAs are versatile and can be applied to a wide range of optimization problems, including those encountered in machine learning, engineering, finance, and other domains 52 . When applied to machine learning tasks, GAs can be used for feature selection, hyperparameter optimization, model tuning, and other optimization challenges encountered in the development and deployment of machine learning systems. Overall, the learning capabilities of GAs make them well-suited for tackling challenging optimization problems in various domains, and they have proven to be effective tools for finding high-quality solutions in diverse applications.
GA framework 54 .
Performance evaluation indices of models
The performance evaluation of a machine learning model for predicting the slope FOS in debris flow is a crucial step in assessing the model's accuracy and reliability 56 . There are some key steps and considerations for evaluating the performance of machine learning models to be considered. Data splitting: Dividing your dataset into training and testing sets. A common split is to use a majority of the data for training (e.g., 80% or 70%) and the rest for testing (e.g., 20% or 30%). Model training: Train your machine learning model using the training dataset. In this case, you would use features related to the debris flow slope FOS as input variables and the actual FOS values as the target variable. Model prediction: Use the trained model to make predictions on the testing dataset 56 . The model will provide predicted values for the slope FOS based on the input features. Performance metrics: Evaluate the model’s performance using appropriate metrics for regression tasks. In the present research work, a multitude of metrics have been applied, including mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), R-squared (R 2 ), weighted mean absolute percentage error (WMAPE), not significant (NS), variance accounted for (VAF), prediction interval (PI), reparameterized slashed Rayleigh (RSR), normalized mean bias error (NMBE), robust partial discriminant analysis (RPDa), mean bias error (NBE), linear matrix inequality (LMI), confidence level within 95% (U95), standard error (t-sta), and genuine progress indicator (GPI). The mathematical expressions for the utilized metrics in this performance evaluation study can be found in statistical texts 56 . Visual inspection: Create visualizations such as scatter plots comparing predicted values against actual values. This can help identify patterns, trends, or potential outliers. Cross-validation: Perform k-fold cross-validation to assess the model's robustness and overfitting issues. This involves splitting the dataset into k subsets and training the model k times, each time using a different subset as the test set 56 . Hyperparameter tuning: Fine-tune the model's hyperparameters to optimize its performance. This can involve adjusting parameters such as the learning rate, tree depth, or regularization. Comparisons: If applicable, compare the performance of your machine learning model with baseline models or other algorithms to ensure that it provides added value 56 . Interpretability: Depending on the complexity of your model, consider assessing its interpretability. Some models, like decision trees, offer easy interpretability, while others, like ensemble methods, may be more complex. By following these steps and metrics, you can comprehensively evaluate the performance of your machine learning model for predicting the debris flow slope FOS. The overall research framework is presented in Fig. 9 .
The overall research plan.
Presentation and analysis of results
Understanding the influence of various factors on the debris flow slope stability FOS involves conducting a comprehensive analysis. Several soil parameters have been studied in this work. Soil unit weight (SUW): Higher SUW generally increases stability, as it contributes to a higher resisting force. However, excessively high SUW may lead to increased loading and could affect stability adversely. Cohesion: A measure of the soil's internal strength; higher cohesion increases stability by providing additional resistance to shearing forces. However, debris flow in some cases may be cohesionless, relying more on frictional resistance. Frictional angle: An increase in the frictional angle between soil particles contributes to higher stability by increasing the resistance to sliding. This is particularly important for understanding the shearing behavior of the soil. Slope angle: As the slope angle increases, the gravitational force component parallel to the slope also increases. Steeper slopes generally reduce stability due to higher driving forces. There is a critical angle beyond which slope failure is more likely. Slope height: Taller slopes may experience higher gravitational forces, potentially reducing stability. The relationship is complex, as other factors like cohesion and frictional angle also come into play. The geometry of the slope can influence how forces are distributed. Pore pressure: Elevated pore pressure within the slope can reduce effective stress, decreasing the soil's shear strength and stability. This is particularly relevant in saturated or partially saturated conditions. To quantitatively assess the influence of these factors, a slope stability analysis using geotechnical engineering principles and methods can be conducted. Numerical modeling or analytical methods, such as the Bishop or Janbu methods, can help estimate the FOS considering these factors. The relationship between these parameters and the FOS may not always be linear, and interactions between different factors should be considered. Empirical relationships derived from field studies and laboratory testing on similar soils can also be valuable for understanding the specific behavior of the debris flow in question. It is essential to note that site-specific conditions, geological characteristics, and the nature of the debris flow material can significantly impact the stability analysis. A thorough geotechnical investigation, including field measurements and laboratory testing, is crucial for accurate slope stability assessments. Figure 10 represents the internal consistency between the output and the studied parameters affecting debris flow down a slope. It can be shown that the consistency between the pore water pressure and the FOS is more concentrated than distributed, which agrees with the conventional principle that states the effect of pore pressure on soil structure within its flow zone. The consistency is more distributed with the shear parameters (cohesion and friction) and slope geometry (slope angle and height). Figures 11 (training set) and 12 (test set) show the graphs between actual and predicted values for the training and testing dataset, where ELM-EO, ELM-HHO, LSSVM-PSO, ANFIS-PSO, and ANFIS-GA have been applied to predict the behavior of FOS considering the influence of the soil parameters and slope geometry. It can be shown that the PSO- and EO-trained predictions produced the most significant outliers from the line of best fit, as illustrated in Fig. 11 a,c,d, while the relationship between the outliers and the line of best fit is more consistent in Fig. 11 b,e. These show the results for the training set. In the test/validation set illustrated in Fig. 12 , the trend is somewhat different because the data cluster is more concentrated at the bottom of the model’s line of best fit. However, the same trend of the outliers’ distribution in Fig. 11 is repeated in Fig. 12 . From the overall performance, as presented in Tables 3 and 4 , the PSO-trained ANFIS model produced an R 2 of 0.8775 in the training set, demonstrating a decisive position consistent with the other indices of performance. In the testing/validation set, it achieved an R 2 of 0.8614, outperforming other techniques. This is because of the ability of the ANFIS-PSO, with its multiple layer configuration, to overcome complex data analysis problems, aligning with the outcomes of previous research exercises 52 , 53 , 54 , 55 . The superior performance of this technique in the prediction of the debris flow slope stability FOS is that the combination of AFNIS and PSO offers several advantages over other machine learning techniques in certain scenarios. ANFIS inherently captures non-linear relationships through the fuzzy rule base 53 . When combined with PSO for parameter optimization, it enhances the model's flexibility in capturing complex and non-linear patterns in the data. This is particularly beneficial when dealing with datasets characterized by intricate relationships 55 . ANFIS provides transparent and interpretable models due to its fuzzy rule base. The linguistic rules in ANFIS are easily understandable, making it suitable for applications where interpretability is crucial, such as in decision support systems or domains where human experts need to comprehend the model's reasoning. ANFIS-PSO is adaptive and capable of self-learning 55 . The combination allows the model to adjust its parameters and rule base to changing patterns in the data. PSO helps optimize the parameters effectively, while the adaptability of ANFIS enables it to continuously refine its knowledge base as new data becomes available 55 . PSO is a global optimization algorithm that explores the entire solution space efficiently. This global search capability is beneficial when dealing with complex, multi-dimensional parameter spaces, as it helps the system avoid getting stuck in local optima 55 . This is particularly advantageous in applications where finding the optimal solution is crucial. Traditional neural networks, especially deep learning models, are often sensitive to the choice of initial parameters 55 . ANFIS-PSO, with its global optimization approach, is generally less sensitive to initialization, making it easier to set up and train compared to certain other machine learning techniques. ANFIS combines symbolic reasoning through fuzzy rules with numeric optimization through PSO. This integration allows for a more robust representation of knowledge in the model, capturing both explicit rules and data-driven patterns. This combination is especially powerful in applications where a hybrid approach is advantageous. ANFIS-PSO often involves fewer hyperparameters compared to some complex machine learning models. The simplicity in parameter tuning can be advantageous in scenarios where ease of implementation and reduced computational cost are priorities. It is important to conclude that the choice of the most suitable machine learning technique depends on the specific characteristics of the problem at hand, the nature of the data, and the goals of the application. While ANFIS-PSO offers advantages in certain contexts, it may not be universally superior and should be carefully considered based on the specific requirements of the task. It is also important to note that previous studies on the FOS of slopes suffering the effects of debris flow and other geophysical flows 27 , 28 , 29 , 30 , 33 , 35 , 36 , 37 , 38 , 39 , 41 , 42 , 44 , 45 , 47 , 48 have not taken the effect of the pore water pressure seriously, neglecting the behavior of the soil water retention characteristics in their exercises. However, in this work, the pore water pressure has been studied as an important factor in the prediction of the debris flow slope FOS.
Correlation plot.
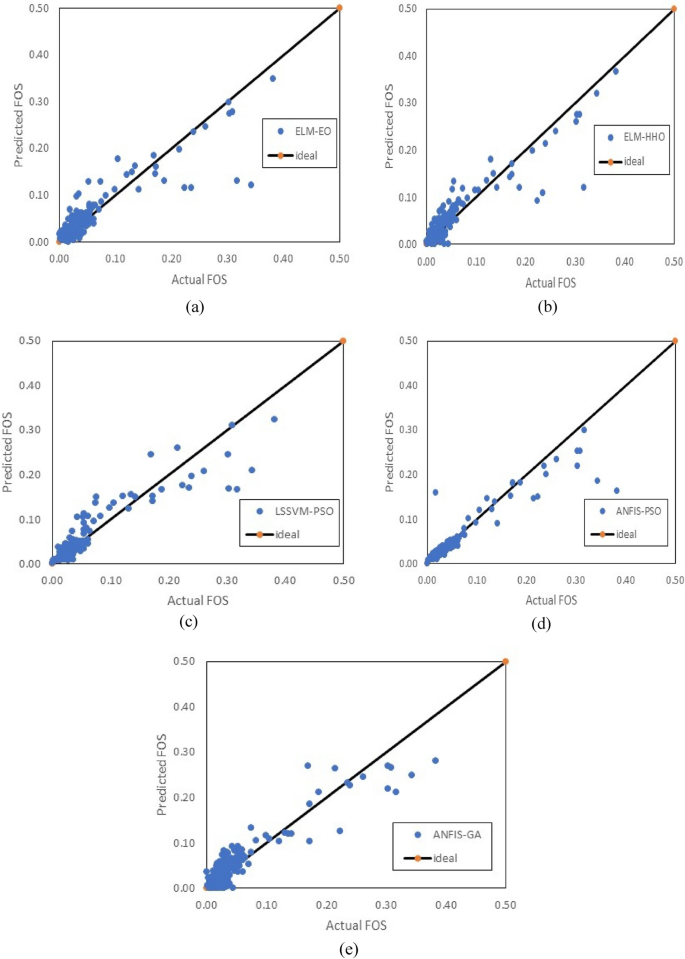
Representation of the graph between actual and predicted values for training dataset ( a ) ELM-EO ( b ) ELM-HHO ( c ) LSSVM-PSO ( d ) ANFIS-PSO and ( e ) ANFIS-GA.
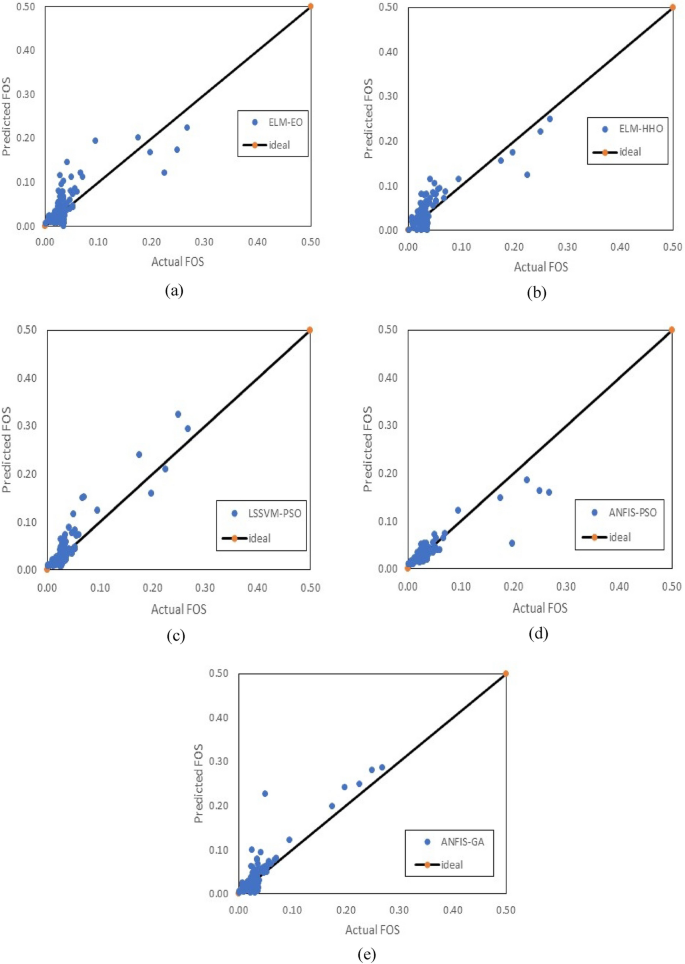
Representation of the graph between actual and predicted values for testing dataset ( a ) ELM-EO ( b ) ELM-HHO ( c ) LSSVM-PSO ( d ) ANFIS-PSO and ( e ) ANFIS-GA.
Conclusions
In this work, an intelligent numerical model of debris flow susceptibility using slope stability failure machine learning FOS prediction with LSSVR, ANFIS, and ELM metaheuristic techniques trained with EO, PSO, HHO, and genetic algorithms has been carried out. The selected input variables were soil unit weight, cohesion, frictional angle, slope angle, slope height, and the pore water pressure of the studied debris flow slope, while the FOS was the target or output. From this study, the following conclusions can be drawn:
The soil parameters and slope geometry have been studied, with reflective field data collected, sorted, and used to predict the behavior of the debris flow susceptibility and slope stability failure FOS, aiming for cost-effecitve and time-saving debris flow design and construction.
Contributions from SUW, cohesion, friction angle, slope angle, slope height, and pore pressure were considered.
The metaheuristic algorithm-trained machine learning techniques showed remarkable performance, exceeding 80%.
The ANFIS-PSO combination produced the best model performance, exceeding 85%, and proved decisive in the prediction of the debris flow susceptibility and slope stability failure FOS.
Data availability
The supporting data for this research project is available from the corresponding author on reasonable request.
Anderson, S. A. & Sitar, N. Analysis of rainfall-induced debris flows. J. Geotech. Eng. 121 (7), 544–552. https://doi.org/10.1061/(asce)0733-9410(1995)121:7(544) (1995).
Article Google Scholar
Kim, H., Lee, S. W., Yune, C.-Y. & Kim, G. Volume estimation of small scale debris flows based on observations of topographic changes using airborne LiDAR DEMs. J. Mountain Sci. 11 (3), 578–591. https://doi.org/10.1007/s11629-013-2829-8 (2014).
Wang, X., Morgenstern, N. R. & Chan, D. H. A model for geotechnical analysis of flow slides and debris flows. Can. Geotech. J. 47 (12), 1401–1414. https://doi.org/10.1139/t10-039 (2010).
Jakob, M. (n.d.). Debris-flow hazard analysis. Springer Praxis Books, 411–443. https://doi.org/10.1007/3-540-27129-5_17
Luna, B. Q. et al. Methods for debris flow hazard and risk assessment. Adv. Nat. Technol. Hazards Res. https://doi.org/10.1007/978-94-007-6769-0_5 (2013).
Ciurleo, M., Mandaglio, M. C., Moraci, N. & Pitasi, A. A method to evaluate debris flow triggering and propagation by numerical analyses. Geotech. Res. Land Protect. Dev. https://doi.org/10.1007/978-3-030-21359-6_4 (2019).
Zhang, N., Matsushima, T. & Peng, N. Numerical investigation of post-seismic debris flows in the epicentral area of the Wenchuan earthquake. Bull. Eng. Geol. Environ. https://doi.org/10.1007/s10064-018-1359-6 (2018).
Hong, M., Jeong, S. & Kim, J. A combined method for modeling the triggering and propagation of debris flows. Landslides https://doi.org/10.1007/s10346-019-01294-5 (2019).
Liu, W., Yang, Z. & He, S. Modeling the landslide-generated debris flow from formation to propagation and run-out by considering the effect of vegetation. Landslides https://doi.org/10.1007/s10346-020-01478-4 (2020).
Rendina, I., Viccione, G. & Cascini, L. Kinematics of flow mass movements on inclined surfaces. Theor. Comput. Fluid Dynam. https://doi.org/10.1007/s00162-019-00486-y (2019).
Article MathSciNet Google Scholar
Kwan, J. S. H., Sze, E. H. Y. & Lam, C. Finite element analysis for rockfall and debris flow mitigation works. Cana. Geotech. J. https://doi.org/10.1139/cgj-2017-0628 (2018).
Li, Y. et al. Numerical investigation of the flow characteristics of Bingham fluid on a slope with corrected smooth particle hydrodynamics. Front. Environ. Sci. 10 , 1060703. https://doi.org/10.3389/fenvs.2022.1060703 (2022).
Moreno, E., Dialami, N. & Cervera, M. Modeling of spillage and debris floods as Newtonian and viscoplastic Bingham flows with free surface with mixed stabilized finite elements. J. Non-Newtonian Fluid Mech. https://doi.org/10.1016/j.jnnfm.2021.104512 (2021).
Qingyun, Z., Mingxin, Z. & Dan, H. Numerical simulation of impact and entrainment behaviors of debris flow by using SPH–DEM–FEM coupling method. Open Geosci. 14 (1), 1020–1047. https://doi.org/10.1515/geo-2022-0407 (2022).
Whipple, K. X. Open-channel flow of bingham fluids: Applications in debris-flow research. J. Geol. 105 (2), 243–262. https://doi.org/10.1086/515916 (1997).
Article ADS Google Scholar
Averweg, S., Schwarz, A., Nisters, C. & Schröder, J. A least-squares finite element formulation to solve incompressible non-Newtonian fluid flow. Proc. Appl. Math. Mech. 20 , e202000169. https://doi.org/10.1002/pamm.202000169 (2021).
Ming-de, S. Finite element analysis of non-Newtonian fluid flow in 2-d branching channel. Appl. Math. Mech. 7 (10), 987–994. https://doi.org/10.1007/bf01907601 (1986).
Böhme, G. & Rubart, L. Non-Newtonian flow analysis by finite elements. Fluid Dynam. Res. 5 (3), 147–158. https://doi.org/10.1016/0169-5983(89)90018-x (1989).
Sváček, P. On approximation of non-Newtonian fluid flow by the finite element method. J. Comput. Appl. Math. 218 (1), 167–174. https://doi.org/10.1016/j.cam.2007.04.040 (2008).
Article ADS MathSciNet Google Scholar
Reddy, M. P. & Reddy, J. N. Finite-element analysis of flows of non-Newtonian fluids in three-dimensional enclosures. Int. J. Non-Linear Mech. 27 (1), 9–26. https://doi.org/10.1016/0020-7462(92)90019-4 (1992).
Quan Luna, B. et al. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 11 (7), 2047–2060. https://doi.org/10.5194/nhess-11-2047-2011 (2011).
Hemeda, S. Geotechnical modelling and subsurface analysis of complex underground structures using PLAXIS 3D. Geo-Eng. 13 , 9. https://doi.org/10.1186/s40703-022-00174-7 (2022).
Melo, R., van Asch, T. & Zêzere, J. L. Debris flow run-out simulation and analysis using a dynamic model. Nat. Hazards Earth Syst. Sci. 18 , 555–570. https://doi.org/10.5194/nhess-18-555-2018 (2018).
Woldesenbet, T. T., Arefaine, H. B. & Yesuf, M. B. Numerical stability analysis and geotechnical investigation of landslide prone area (the case of Gechi district, Western Ethiopia). Environ. Challenges 13 , 100762. https://doi.org/10.1016/j.envc.2023.100762 (2023).
Onyelowe, K. C., Sujatha, E. R., Aneke, F. I. & Ebid, A. M. Solving geophysical flow problems in Luxembourg: SPH constitutive review. Cogent Eng. https://doi.org/10.1080/23311916.2022.2122158 (2022).
Onyelowe, K. C. et al. Innovative overview of SWRC application in modeling geotechnical engineering problems. Designs 2022 (6), 69. https://doi.org/10.3390/designs6050069 (2022).
Moreno, E., Dialami, N. & Cervera, M. Modeling of spillage and debris floods as Newtonian and viscoplastic bingham flows with free surface with mixed stabilized finite elements. J. Non-Newtonian Fluid Mech. 290 , 104512 (2021).
Article MathSciNet CAS Google Scholar
Quan Luna, B. et al. The application of numerical debris flow modelling for the generation of physical vulnerability curves. Nat. Hazards Earth Syst. Sci. 11 (7), 2047–2060 (2011).
Nguyen, L. C., Van Tien, P. & Do, T.-N. Deep-seated rainfall-induced landslides on a new expressway: A case study in Vietnam. Landslides 17 (2), 395–407 (2020).
Bašić, M., Blagojević, B., Peng, C. & Bašić, J. Lagrangian differencing dynamics for time-independent non-Newtonian materials. Materials 14 (20), 6210 (2021).
Article ADS PubMed PubMed Central Google Scholar
Ming-de, Su. Finite element analysis of non-newtonian fluid flow in 2-d branching channel. Appl. Math. Mech. 7 (10), 987–994 (1986).
Lee, S., An, H., Kim, M. & Lim, H. Analysis of debris flow simulation parameters with entrainment effect: A case study in the Mt. Umyeon. J. Korea Water Resour. Assoc. 53 (9), 637–646 (2020).
Google Scholar
Kwan, J. S. H., Sze, E. H. Y. & Lam, C. Finite element analysis for rockfall and debris flow mitigation works. Can. Geotech. J. 56 (9), 1225–1250 (2019).
Martinez, C., Miralles-Wilhelm, F. & Garcia-Martinez, R. Verification of a 2D finite element debris flow model using bingham and cross rheological formulations. WIT Trans. Eng. Sci. 60 , 61–69 (2008).
Martinez, Cora E. 2009. “Eulerian-Lagrangian Two Phase Debris Flow Model.”
Nguyen, Lan Chau, Tuan-Nghia Do, and Quoc Dinh Nguyen. 2023. “Characteristics and Remedy Solutions for a New Mong Sen Deep-Seated Landslide, Sapa Town, Vietnam.” In Progress in Landslide Research and Technology, Volume 1 Issue 2, 2022 , Springer, 403–13.
Negishi, H. et al. Bingham fluid simulations using a physically consistent particle method. J. Fluid Sci. Technol 18 (4), JFST0035–JFST0035 (2023).
Kondo, M., Fujiwara, T., Masaie, I. & Matsumoto, J. A physically consistent particle method for high-viscous free-surface flow calculation. Comput. Part. Mech. https://doi.org/10.1007/s40571-021-00408-y (2021).
Sváček, P. On approximation of non-newtonian fluid flow by the finite element method. J. Comput. Appl. Math. 218 (1), 167–174 (2008).
Licata, I. & Benedetto, E. Navier-Stokes equation and computational scheme for non-newtonian debris flow. J. Comput. Eng. 2014 , 1–5. https://doi.org/10.1155/2014/201958 (2014).
Qingyun, Z., Mingxin, Z. & Dan, H. Numerical simulation of impact and entrainment behaviors of debris flow by using SPH–DEM–FEM coupling method. Open Geosci. 14 (1), 1020–1047 (2022).
Bokharaeian, M., Naderi, R. & Csámer, Á. Numerical experimental comparison of mudflow by smoothed particle hydrodynamics (SPH). Int. Rev. Appl. Sci. Eng. 13 (1), 22–28 (2021).
Böhme, G. & Rubart, L. Non-Newtonian flow analysis by finite elements. Fluid Dynam. Res. 5 (3), 147 (1989).
Rendina, I., Viccione, G. & Cascini, L. Kinematics of flow mass movements on inclined surfaces. Theor. Comput. Fluid Dyn. 33 , 107–123 (2019).
Melo, R., van Asch, T. & Zêzere, J. L. Debris flow run-out simulation and analysis using a dynamic model. Nat. Hazards Earth Syst. Sci. 18 (2), 555–570 (2018).
Reddy, M. P. & Reddy, J. N. Finite-element analysis of flows of non-Newtonian fluids in three-dimensional enclosures. Int. J. Non-linear Mech. 27 (1), 9–26 (1992).
Woldesenbet, T. T., Arefaine, H. B. & Yesuf, M. B. Numerical stability analysis and geotechnical investigation of landslide prone area (the Case of Gechi District, Western Ethiopia). Environ. Challenges 13 , 100762 (2023).
Hemeda, S. Geotechnical modelling and subsurface analysis of complex underground structures using PLAXIS 3D. Int. J. Geo-Eng. 13 (1), 9 (2022).
Whipple, K. X. Open-channel flow of Bingham fluids: Applications in debris-flow research. J. Geol. 105 (2), 243–262 (1997).
Averweg, S., Schwarz, A., Nisters, C. & Schröder, J. A least-squares finite element formulation to solve incompressible non-Newtonian fluid flow. PAMM 20 (1), e202000169 (2021).
Khochtali, H. et al. Comparison of coupled Eulerian-Lagrangian and coupled smoothed particle hydrodynamics-Lagrangian in fluid-structure interaction applied to metal cutting. Arab. J. Sci. Eng. 46 , 11923–11936. https://doi.org/10.1007/s13369-021-05737-x (2021).
Article CAS Google Scholar
Heidari, A. A. et al. Harris hawks optimization: Algorithm and applications. Fut. Gener. Comput. Syst. 97 , 849–872. https://doi.org/10.1016/j.future.2019.02.028 (2019).
Sun, Z., Tao, L., Wang, X. & Zhou, Z. Localization algorithm in wireless sensor networks based on multiobjective particle swarm optimization. Int. J. Distrib. Sensor Netw. https://doi.org/10.1155/2015/716291 (2015).
Lee, C. K. M. et al. Design of a genetic algorithm for bi-objective flow shop scheduling problems with re-entrant jobs. Int. J. Adv. Manuf. Technol. 56 , 1105–1113. https://doi.org/10.1007/s00170-011-3251-4 (2011).
Dubey, A. K., Kumar, A. & Agrawal, R. An efficient ACO-PSO-based framework for data classification and preprocessing in big data. Evol. Intel. 14 , 909–922. https://doi.org/10.1007/s12065-020-00477-7 (2021).
Taylor, S. (2015). Regression analysis; the estimation of relationships between a dependent variable and one or more independent variables, CFI Education Inc.
Download references
Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project Number (RSPD2024R701), King Saud University, Riyadh, Saudi Arabia.
This research is funded by the Researchers Supporting Project Number (RSPD2024R701), King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and affiliations.
Department of Civil Engineering, Michael Okpara University of Agriculture, Umudike, Nigeria
Kennedy C. Onyelowe
Department of Civil Engineering, University of the Peloponnese, 26334, Patras, Greece
Department of Civil Engineering, Kampala International University, Kampala, Uganda
Department of Civil Engineering, National Institute of Technology Warangal, Warangal, 506004, India
Arif Ali Baig Moghal
Civil Engineering Department, National Institute of Technology, Patna, India
Furquan Ahmad
Department of Industrial Engineering, College of Engineering, King Saud University, 11421, Riyadh, Saudi Arabia
Ateekh Ur Rehman
Department of Civil Engineering, Al-Balqa Applied University, As-Salt, Jordan
Shadi Hanandeh
Department of Civil Engineering, Louisiana Transportation Research Centre (LTRC), Louisiana State University, Baton Rouge, LA, 70803, USA
You can also search for this author in PubMed Google Scholar
Contributions
KCO conceptualized the research work, KCO, AABM, FA, AUR and SH wrote the manuscript, and KCO prepared the figures. All the authors reviewed the manuscript. The consent of the authors is given for the publication of this research paper.
Corresponding author
Correspondence to Kennedy C. Onyelowe .
Ethics declarations
Competing interests.
The authors declare no competing interests.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/ .
Reprints and permissions
About this article
Cite this article.
Onyelowe, K.C., Moghal, A.A.B., Ahmad, F. et al. Numerical model of debris flow susceptibility using slope stability failure machine learning prediction with metaheuristic techniques trained with different algorithms. Sci Rep 14 , 19562 (2024). https://doi.org/10.1038/s41598-024-70634-w
Download citation
Received : 26 January 2024
Accepted : 20 August 2024
Published : 22 August 2024
DOI : https://doi.org/10.1038/s41598-024-70634-w
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Debris flow
- Slope failure
- Factor of safety (FOS)
By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

COMMENTS
Numerical Analysis. The area of numerical analysis is also known as numerical computation, numerical methods, numerical mathematics, computational mathematics, scientific computing or mathematical software, depending on which aspect of this broad subject is being emphasized. One can argue that the reason computers were invented was to perform ...
The soul of numerical simulation is numerical method, which is driven by the above demands and in return pushes science and technology by the successful applications of advanced numerical methods. With the development of mathematical theory and computer hardware, various numerical methods are proposed.
Python Programming And Numerical Methods: A Guide For Engineers And Scientists This notebook contains an excerpt from the Python Programming and Numerical Methods - A Guide for Engineers and Scientists, the content is also available at Berkeley Python Numerical Methods.
VeriNum. In this collection of research projects, we take a layered approach to foundational verification of correctness and accuracy of numerical software-that is, formal machine-checked proofs about programs (not just algorithms), with no assumptions except specifications of instruction-set architectures.
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics ). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones.
Preface This book grew out of the course on fundamental numerical methods that I have been teaching at the University of Maryland for several years. While some of the students in this class will do their PhD in some area of computational science, the majority focus their research on other topics and take the course to learn the fundamentals of numerical methods. Given this, my experience is ...
Explore the latest full-text research PDFs, articles, conference papers, preprints and more on NUMERICAL METHODS. Find methods information, sources, references or conduct a literature review on ...
This engineering mathematics journal covers a wide range of fundamental and emerging concepts in computational science and engineering. IJNME is the home for difference-making research, and we champion research on significant developments in all types of numerical methods, leading to global engineering solutions and progress.
Computational Science & Numerical Analysis. Computational science is a key area related to physical mathematics. The problems of interest in physical mathematics often require computations for their resolution. Conversely, the development of efficient computational algorithms often requires an understanding of the basic properties of the ...
This course offers an advanced introduction to numerical analysis, with a focus on accuracy and efficiency of numerical algorithms. Topics include sparse-matrix/iterative and dense-matrix algorithms in numerical linear algebra (for linear systems and eigenproblems), floating-point arithmetic, backwards error analysis, conditioning, and stability.
Introduction to numerical methods, or techniques to approximate mathematical processes such as integrals, differential equations, or nonlinear equations when the procedure cannot be solved …
In this research paper, i explore some of the most common numerical and analytical methods for solving ordinary differential equations.
methods for approximating all the zeros of a polynomial simultaneously (see, e.g., [8-11]). Let us recall the two most popular iterative methods for simultaneous computation of all the zeros of a polynomial f of degree n ≥2. These are Weierstrass' method [12] and Ehrlich's method [13]. Weierstrass' method is defined by the following ...
Quantitative research is the process of collecting and analyzing numerical data. It can be used to find patterns and averages, make predictions, test causal relationships, and generalize results to wider populations.
Definition Quantitative methods emphasize objective measurements and the statistical, mathematical, or numerical analysis of data collected through polls, questionnaires, and surveys, or by manipulating pre-existing statistical data using computational techniques. Quantitative research focuses on gathering numerical data and generalizing it across groups of people or to explain a particular ...
Aitken's delta-squared process — most useful for linearly converging sequences. Minimum polynomial extrapolation — for vector sequences. Richardson extrapolation. Shanks transformation — similar to Aitken's delta-squared process, but applied to the partial sums. Van Wijngaarden transformation — for accelerating the convergence of an ...
The dynamics of innumerable real-world phenomena is represented with the help of non-linear ordinary differential equations (NODEs). There is a growing trend of solving these equations using accurate and easy to implement methods. The goal of this research work is to create a numerical method to solve the first-order NODEs (FNODEs) by coupling of the well-known trapezoidal method with a newly ...
Here are some key characteristics of quantitative research: Numerical data: Quantitative research involves collecting numerical data through standardized methods such as surveys, experiments, and observational studies. This data is analyzed using statistical methods to identify patterns and relationships.
All Answers (5) Lokesh Gagnani. Kalol Institute of Technology & Research Centre. For Numerical Analysis projects at undergraduate level students can be given various animations projects for Root ...
The International Journal for Numerical Methods in Fluids is a leading fluid mechanics journal publishing computational methods applied to fluid mechanics & dynamics. Summary We propose an implicit discontinuous Galerkin (DG) discretization for incompressible two-phase flows using an artificial compressibility formulation.
The emphasis will be on the breadth of topics and applications; however, to the extent possible, the mathematical theory behind the numerical methods will also be presented. The course is expected to lay foundation for students beginning to engage in research projects that involve numerical methods. Student will use MATLAB as a tool in the course.
Project presentations take place on a Saturday, and are aimed at a general scientific audience, with focus on the numerical solution of physically arising equations. The following represents the project abstracts chosen by the students during the Spring '09 term.
The following projects are based on numerical methods. This list shows the latest innovative projects which can be built by students to develop hands-on experience in areas related to/ using numerical methods. 1. A Numerical Solution to 2D Flat Plate Problem with Constant Conductivity Heat Transfer. All the engineering devices we use involves ...
Numerical analysis plays a crucial role in modern science and engineering. It helps solve problems that are too complex for analytical methods. Here are some real-life applications of numerical analysis: Weather Forecasting. Predicting weather involves complex calculations.
In this work, intelligent numerical models for the prediction of debris flow susceptibility using slope stability failure factor of safety (FOS) machine learning predictions have been developed.