
- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt

Linear Sum Assignment Solver
This section describes the linear sum assignment solver , a specialized solver for the simple assignment problem, which can be faster than either the MIP or CP-SAT solver. However, the MIP and CP-SAT solvers can handle a much wider array of problems, so in most cases they are the best option.
Cost matrix
The costs for workers and task are given in the table below.
| Worker | Task 0 | Task 1 | Task 2 | Task 3 |
|---|---|---|---|---|
| 90 | 76 | 75 | 70 | |
| 35 | 85 | 55 | 65 | |
| 125 | 95 | 90 | 105 | |
| 45 | 110 | 95 | 115 |
The following sections present a Python program that solves an assignment problem using the linear sum assignment solver.
Import the libraries
The code that imports the required library is shown below.
Define the data
The following code creates the data for the program.
The array is the cost matrix , whose i , j entry is the cost for worker i to perform task j . There are four workers, corresponding to the rows of the matrix, and four tasks, corresponding to the columns.
Create the solver
The program uses the linear assignment solver, a specialized solver for the assignment problem.
The following code creates the solver.
Add the constraints
The following code adds the costs to the solver by looping over workers and tasks.
Invoke the solver
The following code invokes the solver.
Display the results
The following code displays the solution.
The output below shows the optimal assignment of workers to tasks.
The following graph shows the solution as the dashed edges in the graph. The numbers next to the dashed edges are their costs. The total wait time of this assignment is the sum of the costs for the dashed edges, which is 265.
In graph theory, a set of edges in a bipartite graph that matches every node on the left with exactly one node on the right is called a perfect matching .
The entire program
Here is the entire program.
Solution when workers can't perform all tasks
In the previous example, we assumed that all workers can perform all tasks. But this not always the case - a worker might be unable to perform one or more tasks for various reasons. However, it is easy to modify the program above to handle this.
As an example, suppose that worker 0 is unable to perform task 3. To modify the program to take this into account, make the following changes:
- Change the 0, 3 entry of the cost matrix to the string 'NA' . (Any string will work.) cost = [[90, 76, 75, 'NA'], [35, 85, 55, 65], [125, 95, 90, 105], [45, 110, 95, 115]]
- In the section of the code that assigns costs to the solver, add the line if cost[worker][task] != 'NA': , as shown below. for worker in range(0, rows): for task in range(0, cols): if cost[worker][task] != 'NA': assignment.AddArcWithCost(worker, task, cost[worker][task]) The added line prevents any edge whose entry in the cost matrix is 'NA' from being added to the solver.
After making these changes and running the modified code, you see the following output:
Notice that the total cost is higher now than it was for the original problem. This is not surprising, since in the original problem the optimal solution assigned worker 0 to task 3, while in the modified problem that assignment is not allowed.
To see what happens if more workers are unable to perform tasks, you can replace more entries of the cost matrix with 'NA' , to denote additional workers who can't perform certain tasks:
When you run the program this time, you get a negative result:
This means there is no way to assign workers to tasks so that each worker performs a different task. You can see why this is so by looking at the graph for the problem (in which there are no edges corresponding to values of 'NA' in the cost matrix).
Since the nodes for the three workers 0, 1, and 2 are only connected to the two nodes for tasks 0 and 1, it not possible to assign distinct tasks to these workers.
The Marriage Theorem
There is a well-known result in graph theory, called The Marriage Theorem , which tells us exactly when you can assign each node on the left to a distinct node on the right, in a bipartite graph like the one above. Such an assignment is called a perfect matching . In a nutshell, the theorem says this is possible if there is no subset of nodes on the left (like the one in the previous example ) whose edges lead to a smaller set of nodes on the right.
More precisely, the theorem says that a bipartite graph has a perfect matching if and only if for any subset S of the nodes on the left side of the graph, the set of nodes on the right side of the graph that are connected by an edge to a node in S is at least as large as S.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2024-08-28 UTC.
- Docs »
- 4. API ( l-o ) »
- 4.5. Optimization and root finding ( scipy.optimize ) »
- 4.5.4.4. scipy.optimize.linear_sum_assignment
- View page source
4.5.4.4. scipy.optimize.linear_sum_assignment ¶
Solve the linear sum assignment problem.
The linear sum assignment problem is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a “worker”) and vertex j of the second set (a “job”). The goal is to find a complete assignment of workers to jobs of minimal cost.
Formally, let X be a boolean matrix where \(X[i,j] = 1\) iff row i is assigned to column j. Then the optimal assignment has cost
s.t. each row is assignment to at most one column, and each column to at most one row.
This function can also solve a generalization of the classic assignment problem where the cost matrix is rectangular. If it has more rows than columns, then not every row needs to be assigned to a column, and vice versa.
The method used is the Hungarian algorithm, also known as the Munkres or Kuhn-Munkres algorithm.
| Parameters: | : array |
|---|---|
| Returns: | : array col_ind].sum(). The row indices will be sorted; in the case of a square cost matrix they will be equal to . |
New in version 0.17.0.
- http://www.public.iastate.edu/~ddoty/HungarianAlgorithm.html
- Harold W. Kuhn. The Hungarian Method for the assignment problem. Naval Research Logistics Quarterly , 2:83-97, 1955.
- Harold W. Kuhn. Variants of the Hungarian method for assignment problems. Naval Research Logistics Quarterly , 3: 253-258, 1956.
- Munkres, J. Algorithms for the Assignment and Transportation Problems. J. SIAM , 5(1):32-38, March, 1957.
- https://en.wikipedia.org/wiki/Hungarian_algorithm
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Linear sum assignment, but with ranked assignments?
Let's say I have 5 tasks that I have to assign to 5 agents, with a cost matrix:
Using scipy's optimization library, I can get assignments for each agent:
However, what if I'm only interested in the agents to assign task 0? Let's say I just want to understand for task 0 only a ranked list of agents to assign to that task, but still with the goal of minimizing total system-wide cost. Is there any way to solve for this problem?
- linear-programming
- combinatorial-optimization
- assignment-problem
- 2 $\begingroup$ What about maybe solving the LAP n(umber agents) times, while each iteration fixes a different agent to task 0. Rank by objective-values after. I guess such partial-fixing should be trivial given a LP-based LAP-solver (a variable-bound of [1,1] instead of [0,1] doesn't destroy any relevant structure, e.g. total unimodularity). (One could even exploit warm-start / incrementality to speed it up i guess) $\endgroup$ – sascha Commented May 21 at 1:34
- 1 $\begingroup$ @sascha Ended up going with this approach! Added benefit is that I was able to run iterations in parallel thereby reducing runtime. $\endgroup$ – Dan Commented May 31 at 17:21
Know someone who can answer? Share a link to this question via email , Twitter , or Facebook .
Your answer, sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Browse other questions tagged linear-programming python combinatorial-optimization assignment-problem or ask your own question .
- Featured on Meta
- Bringing clarity to status tag usage on meta sites
- Announcing a change to the data-dump process
Hot Network Questions
- A short story about a boy who was the son of a "normal" woman and a vaguely human denizen of the deep
- Journal keeps messing with my proof
- Explain how π – 1 + 50 + ⅔ × 1000 is PLONK
- 2 in 1: Twin Puzzle
- What happens when touching a piece which cannot make a legal move?
- How to define a function for Schmitt trigger?
- Modify lplfitch proof style
- Word for a collection of awards, such as an Olympic athlete’s earned medals
- Maximizing the common value of both sides of an equation
- What is the highest apogee of a satellite in Earth orbit?
- Writing an i with a line over it instead of an i with a dot and a line over it
- Who is the referent of "him" in Genesis 18:2?
- How specific does the GDPR require you to be when providing personal information to the police?
- Coding exercise to represent an integer as words using python
- How much new mathematics should we learn during the PhD? Are the courses we take during the PhD really important?
- What is this device in my ceiling making out of battery chirps?
- magnetic boots inverted
- How do eradicated diseases make a comeback?
- Why is simpler prose more popular these days?
- A SF novel where one character makes a "light portrait" of another one, with huge consequences
- How can one be honest with oneself if one IS oneself?
- What counts as the Earth's mass? At which point would it increase or decrease?
- Encode a VarInt
- How can judicial independence be jeopardised by politicians' criticism?
Navigation Menu
Search code, repositories, users, issues, pull requests..., provide feedback.
We read every piece of feedback, and take your input very seriously.
Saved searches
Use saved searches to filter your results more quickly.
To see all available qualifiers, see our documentation .
- Notifications You must be signed in to change notification settings
Benchmarking Linear Assignment Problem Solvers
berhane/LAP-solvers
Folders and files.
| Name | Name | |||
|---|---|---|---|---|
| 63 Commits | ||||
Repository files navigation
The script benchmarks the performance of Python3 linear assignment problem solvers for random cost matrices of different sizes. These solvers are:
- https://github.com/scipy/scipy/
- https://github.com/bmc/munkres
- does not work with Python 3.6 and 3.7
- https://github.com/Hrldcpr/Hungarian
- https://github.com/gatagat/lap In addition, these two solvers are added for Python3
- Please see the blog post here
- https://github.com/src-d/lapjv
- Please note that Christioph has also done a benchmark of LAP solvers
- https://github.com/cheind/py-lapsolver
- https://github.com/jdmoorman/laptools
They all formally have O(n 3 ) complexity, but their performance differs substantially based on their implementation and the size of the matrix they are trying to solve. The solvers can be classified based on some unique characteristics.
| Module | Python or C/C++/Cython | Algorithm |
|---|---|---|
| scipy.optimize.linear_sum_assignment | Python(<v1.4)/C++(=>v1.4)) | Hungarian |
| munkres.Munkres | Python | Hungarian |
| laptools.clap | Python | ? |
| hungarian.lap | C++ | Hungarian |
| lap.lapjv | C++ | Jonker-Volgenant |
| lapjv.lapjv | C++ | Jonker-Volgenant |
| lapsolver.solve_dense | C++ | shortest augmenting path |
The purpose of this benchmarking exercise is to see which implementation performs best for a given matrix size. My interest is to use this information to improve the performance of Arbalign and expand its use.
The repo contains the following:
- benchmark-lap-solvers.py - a Python3 script comparing four/six implementations
- benchmark-lap-solvers-py3.ipynb - a Jupyter notebook comparing four/six implementations. It has been tested using Python 3.6 and 3.7.
It's simple once you have installed the necessary packages.
| command | execution | note |
|---|---|---|
| default | ||
| default, except it looks at small matrices only | ||
| default, except plotting is suppressed | ||
| default, except it prints lowest cost for each method |
If you want to add other solvers to the list, it should be easy to figure out what parts to update in the scripts.
Requirements
- pip3 install numpy
- conda install numpy
- pip3 install matplotlib
- conda install matplotlib
- pip3 install scipy==1.4
- conda install scipy
- pip3 install munkres
- conda install munkres
- pip3 install hungarian
- conda install -c psi4 hungarian
- pip3 install lap
- conda install lap
- pip3 install lapjv
- pip3 install lapsolver
- conda install -c loopbio lapsolver
- pip3 install laptools (Python 3.5+)
The script will produce output similar to what's shown below. Some things to note are:
- The timings here corresponds to an average of three Python 3.5.6 runs on CentOS 7 machine with 2.4 GHz Intel Xeon Gold 6148 processor and 192GB of RAM
- The random matrices are filled with floating point numbers ranging from 0 to the size (# of rows or columns) of the matrix. They are generated using numpy: cost_matrix = matrix_size * np.random.random((matrix_size, matrix_size))
- Data of timing for solving LAP of random cost matrices of sizes 2 min x 2 min to 2 max x 2 max .
- plot of timing for LAP solving random cost matrices of sizes 2 min x 2 min to 2 max x 2 max , where min and max are limited to smaller numbers for munkres and scipy in the interest of time.

If requested via the --printcost flag, it will also print the minimum cost for each random cost matrix by each implementation. This test ensures that the methods are making consistent/correct assignments.
- scipy==1.4 is much faster than previous versions and it is competitive with the other implementations, especially for larger matrices. This is a great development since it probably gets used more than the other implementations by virtue of scipy's popularity.
- munkres is much slower than hungarian , lapsolver , scipy , lap.lapjv , and lapjv.lapjv for all matrix sizes
- hungarian performs well for smaller matrices. For anything larger than 256x256, lapsolver , lap.lapjv and lapjv.lapjv are about an order of magnitude faster than hungarian
- lap.lapjv is am implementation intended to solve dense matrices. Its sparse matrix solver analog named lap.lapmod is more efficient for larger sparse matrices. Both are implemented in the lap module.
- lapjv.lapjv has the best performance virtually for all matrix sizes.
- For the purposes of improving Arbalign , hungarian remains a good choice for most molecular systems I'm interested in which don't have more than 100x100 distance matrices the same type to solve. However, if the tool is to be applied to larger molecules such as proteins and DNA, it would be worthwhile to use lapjv.lapjv , lapsolver , lap.lapjv or lap.lapmod
- Jupyter Notebook 89.4%
- Python 10.6%
Linear assignment with non-perfect matching
Dec 8, 2020
The linear assignment problem (or simply assignment problem) is the problem of finding a matching between two sets that minimizes the sum of pair-wise assignment costs. This can be expressed as finding a matching (or independent edge set) in a bipartite graph \(G = (U, V, E)\) that minimizes the sum of edge weights. The edge weights may be positive or negative and the bipartite graph does not need to be complete : if there is no edge between two vertices then they cannot be associated. Note that a maximum-weight assignment can be obtained by negating the weights and finding a minimum-weight assignment.
The simplest form of the assignment problem assumes that the bipartite graph is balanced (the two sets of vertices are the same size) and that there exists a perfect matching (in which every vertex has a match). Let \(n\) be the number of elements in each set and let \(C\) be a square matrix of size \(n \times n\) that contains the edge weights. Missing edges are represented by \(\infty\), such that \(C_{i j} < \infty \Leftrightarrow (i, j) \in E\). The assignment problem can then be clearly expressed as an integer linear program : (note that the problem is not actually solved using a general-purpose ILP solver, it is just a convenient framework in which to express the problem)
The constraint that the sum of each row and column is equal to one ensures that each element has exactly one match. However, what happens when the graph is not balanced or does not contain a perfect matching? We cannot enforce the sums to be equal to one. Which problem should be solved?
I recommend reading the tech report “On Minimum-Cost Assignments in Unbalanced Bipartite Graphs” by Lyle Ramshaw and Robert E. Tarjan. I will summarize some of the main points here.
Let us consider a more general, rectangular problem of size \(r \times n\) and assume (without loss of generality) that \(r \le n\). If \(r = n\) then the problem is balanced, if \(r < n\) it is unbalanced.
Clearly an unbalanced probem cannot have a perfect matching, since there will be at least \(n - r\) unmatched elements in the larger set. However, it may be possible to find a matching in which every vertex in the smaller set has a match. This is referred to as a one-sided perfect matching and the optimization problem can be expressed:
The inequality constraints enforce that each element in the smaller set has exactly one match while each element in the larger set has at most one match. Ramshaw and Tarjan outline a method to reduce from an unbalanced problem to a balanced problem while preserving sparsity. A simple alternative is to add \(n - r\) rows of zeros and then exclude these edges from the eventual solution. Most libraries for the assignment problem solve either the balanced or unbalanced version of this problem (see the later section).
However, whether balanced or unbalanced, it may still occur that the constraint set is infeasible, meaning that there does not exist a (one-sided) perfect matching. Let \(\nu(W) \le r\) denote the size of the largest matching in the graph. If \(\nu(W) < r\), then there does not exist a one-sided perfect matching and all possible matchings are imperfect.
Ramshaw and Tarjan actually outline three different versions of the assignment problem:
- perfect matching
- imperfect matching
- minimum-weight matching
The imperfect matching problem is to find the matching of size \(\nu(G)\) with the minimum cost. The minimum-weight matching problem is to find the matching of any size with the minimum cost. If \(\nu(G) = r = n\), then perfect and imperfect matching coincide. Otherwise, when \(\nu(G) < n\), there does not exist a perfect matching.
The imperfect matching problem can be expressed
and the minimum-weight matching problem can be expressed
Ramshaw and Tarjan show that both of these problems can be reduced to finding a perfect matching in a balanced graph. When using linear assignment, we should carefully consider which of the three problems we actually want to solve.
In support of minimum-weight matching
The minimum-weight matching problem is often the most natural choice, since it puts no constraint on the size of the matching. To illustrate the difference between this and the other problems, consider the following balanced problem:
The solution to perfect (or imperfect) matching is to choose -1 and -2 for a total score of -3 and a cardinality of 2. The solution to minimum-weight matching is to choose -4 with a cardinality of 1.
Minimum-weight matching will never select an edge with positive cost: it is better to simply leave it unselected. Edges with zero cost have no impact.
It may be more natural to consider the maximization of positive weights than the minimization of negative costs.
Min-cost imperfect matching with positive weights
Be careful when solving imperfect matching problems with positive edge weights! I would avoid this situation altogether due to the tension that exists between maximizing the number of matches and minimizing the sum of (positive) costs. This may result in the unexpected behaviour that adding an edge to the graph increases the minimum cost. For example, compare the following two problems:
Quick and dirty transformations
Ramshaw and Tarjan above describes some clever techniques to transform imperfect and minimum-weight matching problems into perfect matching problems while preserving sparsity. Here we describe some quick and dirty alternatives.
We can always transform an unbalanced (and therefore imperfect) problem into a balanced problem by adding \(n - r\) rows of zeros. The resulting balanced graph has a perfect matching if and only if the original unbalanced graph had a matching of size \(r\) (in which every vertex in the smaller set is matched).
If we need to solve imperfect matching but we only have a solver for perfect matching, it suffices to replace the infinite edge weights with a large, finite cost (e.g. larger than the total absolute value of all weights). The resulting graph must contain a perfect matching since it is a complete bipartite graph, and each high-cost edge is worth more than all original edges combined. The high-cost edges can be excluded at the end.
Most existing packages either solve perfect, one-sided perfect or imperfect matching. To use one of these solvers for the minimum-weight matching problem, it suffices to replace all positive edges (including infinite edges) with zero. If using a solver that leverages sparsity, it is better to use the technique described by Ramshaw and Tarjan.
Python packages
The table below outlines the different behaviour of several popular packages. The code that was used to determine the behaviour is available as a Jupyter notebook .
| Module | Function | Behaviour |
|---|---|---|
| Requires that problem is balanced (or else raises an exception). Requires that a perfect matching exists (or else returns infinite cost). | ||
| Supports unbalanced problems (with ; although check issues , ). Requires that a one-sided perfect matching exists (or else returns infinite cost). | ||
| Supports unbalanced problems. Requires that a one-sided perfect matching exists (or else raises an exception). | ||
| Supports unbalanced problems. Supports imperfect matching. | ||
| Requires problem is balanced. Requires that a perfect matching exists (or else raises an exception). Requires that costs are integer-valued. |
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Is there an algorithm for solving a many-to-one assignment problem?
I'm looking for an algorithm to solve assignment problem, but it is not one to one problem. I know the Hungarian algorithm it can simply assign one task to one agent.
Let's say I have 4 tasks and 20 agents and I want to assign 5 agents to each task (based on the cost matrix). Is there any efficient algorithm to do this?
It will be great if there is a Python library with algorithm like that.
- optimization
2 Answers 2
Let's say that you now have a 20 by 4 cost matrix $C$ consisting of the costs of assigning agents to tasks. You can make 5 new tasks, each requiring one agent, out of each original task.
To do this, make a new cost matrix $C_{\text{new}}$ , which is 20 by 20, in which each column of $C$ appears 5 times. Use the Hungarian algorithm on $C_{\text{new}}$ . and you will have 1 agent assigned to every new task, which will therefore be 5 agents assigned to every original task.
Using the matrix scheme suggested by Mark, you could use the Jonker-Volgenant algorithm which is a modification of the Hungarian algorithm.
It is implemented in scipy.optimize.linear_sum_assignment . Here is an example from the documentation, which you can modify to include your own choice of cost matrix.
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged optimization algorithms or ask your own question .
- Featured on Meta
- Announcing a change to the data-dump process
- Bringing clarity to status tag usage on meta sites
Hot Network Questions
- Which version of Netscape, on which OS, appears in the movie “Cut” (2000)?
- Cannot open and HTML file stored on RAM-disk with a browser
- Is there a phrase for someone who's really bad at cooking?
- Can IRS make the taxpayer pay the costs of litigation if the latter loses the case?
- My supervisor wants me to switch to another software/programming language that I am not proficient in. What to do?
- Duties when bringing Canadian goods to US in luggage
- Unable to update ubuntu 24.04 after incorrectly installing debian key
- How do eradicated diseases make a comeback?
- How important is philosophy: does anyone delimit its importance?
- How can I get around 16 electrical receptacles in a small area with the least amount of wiring?
- Is there a way to isolate 2 operating systems on 2 different hard drives?
- Can you use 'sollen' the same way as 'should' in sentences about possibility that something happens?
- Which hash algorithms support binary input of arbitrary bit length?
- Whatever happened to Chessmaster?
- Seinfeldisms in O.R
- Has a tire ever exploded inside the Wheel Well?
- Can we make a true \phantom?
- Why is simpler prose more popular these days?
- Determining Error Rate of Phase Shift Keying via Monte Carlo Simulation
- Causal Reconciliation: Is this a viable way for my FTL system to preserve the course of History?
- A SF novel where one character makes a "light portrait" of another one, with huge consequences
- What does this translated phrase convey "The heart refuses to obey."?
- Do passengers transiting in YVR (Vancouver) from international to US go through Canadian immigration?
- Writing an i with a line over it instead of an i with a dot and a line over it
scipy.optimize.linear_sum_assignment #
Solve the linear sum assignment problem.
The cost matrix of the bipartite graph.
Calculates a maximum weight matching if true.
An array of row indices and one of corresponding column indices giving the optimal assignment. The cost of the assignment can be computed as cost_matrix[row_ind, col_ind].sum() . The row indices will be sorted; in the case of a square cost matrix they will be equal to numpy.arange(cost_matrix.shape[0]) .
for sparse inputs
The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a ‘worker’) and vertex j of the second set (a ‘job’). The goal is to find a complete assignment of workers to jobs of minimal cost.
Formally, let X be a boolean matrix where \(X[i,j] = 1\) iff row i is assigned to column j. Then the optimal assignment has cost
where, in the case where the matrix X is square, each row is assigned to exactly one column, and each column to exactly one row.
This function can also solve a generalization of the classic assignment problem where the cost matrix is rectangular. If it has more rows than columns, then not every row needs to be assigned to a column, and vice versa.
This implementation is a modified Jonker-Volgenant algorithm with no initialization, described in ref. [2] .
New in version 0.17.0.
https://en.wikipedia.org/wiki/Assignment_problem
DF Crouse. On implementing 2D rectangular assignment algorithms. IEEE Transactions on Aerospace and Electronic Systems , 52(4):1679-1696, August 2016, DOI:10.1109/TAES.2016.140952
- MapReduce Algorithm
- Linear Programming using Pyomo
- Networking and Professional Development for Machine Learning Careers in the USA
- Predicting Employee Churn in Python
- Airflow Operators

Solving Assignment Problem using Linear Programming in Python
Learn how to use Python PuLP to solve Assignment problems using Linear Programming.
In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.
If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.
The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.
In this tutorial, we are going to cover the following topics:

Assignment Problem
A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.
For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.
Problem Formulation
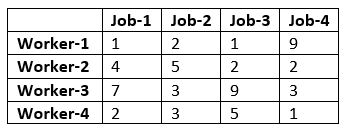
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.
Initialize LP Model
In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.
Define Decision Variable
In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using LpVariable.dicts() class. LpVariable.dicts() used with Python’s list comprehension. LpVariable.dicts() will take the following four values:
- First, prefix name of what this variable represents.
- Second is the list of all the variables.
- Third is the lower bound on this variable.
- Fourth variable is the upper bound.
- Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are LpContinuous or LpInteger .
Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.
Define Objective Function
In this step, we will define the minimum objective function by adding it to the LpProblem object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.
Define the Constraints
Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem object.
Solve Model
In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.
From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.
In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in this article and learn about Linear Programming in this article .
- Solving Blending Problem in Python using Gurobi
Transshipment Problem in Python Using PuLP
You may also like.

Pandas Series

Python Decorators
linear_sum_assignment #
Solve the linear sum assignment problem.
The cost matrix of the bipartite graph.
Calculates a maximum weight matching if true.
An array of row indices and one of corresponding column indices giving the optimal assignment. The cost of the assignment can be computed as cost_matrix[row_ind, col_ind].sum() . The row indices will be sorted; in the case of a square cost matrix they will be equal to numpy.arange(cost_matrix.shape[0]) .
for sparse inputs
The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a ‘worker’) and vertex j of the second set (a ‘job’). The goal is to find a complete assignment of workers to jobs of minimal cost.
Formally, let X be a boolean matrix where \(X[i,j] = 1\) iff row i is assigned to column j. Then the optimal assignment has cost
where, in the case where the matrix X is square, each row is assigned to exactly one column, and each column to exactly one row.
This function can also solve a generalization of the classic assignment problem where the cost matrix is rectangular. If it has more rows than columns, then not every row needs to be assigned to a column, and vice versa.
This implementation is a modified Jonker-Volgenant algorithm with no initialization, described in ref. [2] .
Added in version 0.17.0.
https://en.wikipedia.org/wiki/Assignment_problem
DF Crouse. On implementing 2D rectangular assignment algorithms. IEEE Transactions on Aerospace and Electronic Systems , 52(4):1679-1696, August 2016, DOI:10.1109/TAES.2016.140952

Linear graphlet models for accurate and interpretable cheminformatics †

First published on 16th August 2024
Advances in machine learning have given rise to a plurality of data-driven methods for predicting chemical properties from molecular structure. For many decades, the cheminformatics field has relied heavily on structural fingerprinting, while in recent years much focus has shifted toward leveraging highly parameterized deep neural networks which usually maximize accuracy. Beyond accuracy, to be useful and trustworthy in scientific applications, machine learning techniques often need intuitive explanations for model predictions and uncertainty quantification techniques so a practitioner might know when a model is appropriate to apply to new data. Here we revisit graphlet histogram fingerprints and introduce several new elements. We show that linear models built on graphlet fingerprints attain accuracy that is competitive with the state of the art while retaining an explainability advantage over black-box approaches. We show how to produce precise explanations of predictions by exploiting the relationships between molecular graphlets and show that these explanations are consistent with chemical intuition, experimental measurements, and theoretical calculations. Finally, we show how to use the presence of unseen fragments in new molecules to adjust predictions and quantify uncertainty.
1 Introduction
Model interpretability is often invaluable when ML is applied in the sciences both because it helps scientists understand when and how models make errors, thereby building trust in model predictions, and because it can help uncover trends in predictions, which can lead to enhanced scientific understanding. Methods for interpreting ML models in the context of chemistry and materials problems are reviewed thoroughly in ref. 18 , 20 and we review key points here. In the ML interpretability literature, intrinsically interpretable models 18,20 are those wherein the model functional form and mechanisms for prediction are transparent and meaningful. An often-cited example of such a model is linear regression, where each coefficient has a clear interpretation as the contribution of an individual feature to a prediction (even when these features may be difficult to interpret). In contrast, many ML models – e.g. , deep neural networks (DNNs) – are too large or complicated to be interpreted directly and are thus referred to as black-box methods. Such methods can still be interpreted through post hoc procedures which are applied to models after training or to their predictions. Examples of such techniques include local linear surrogates which examine the contribution of input features near a given input point 21 and similar local explanations called SHapley Additive exPlanations (SHAP) based on game-theory. 22–24 DNNs are often interpreted by methods that examine the gradients of their predictions, e.g. through integrated gradients 25 or the deep Taylor decomposition. 26 Such post hoc methods have been applied to molecular property prediction and have been used to give explanations in terms of atoms, 27 bonds, 28 and higher-order molecular subgraphs. 29
Some argue that because DNNs often provide the most accuracy across ML models and that numerous post hoc DNN explanation methods exist, these methods should be favored over intrinsically explainable models, which are commonly thought to be comparatively weak predictors. 18 However, this perceived accuracy-interpretability tradeoff is often exaggerated and is sometimes orthogonal to observed trends. 19 Furthermore, many post hoc interpretability methods have theoretical weaknesses that are empirically borne out by counter-intuitive and untrustworthy explanations. For example, ref. 30 discusses that numerous post hoc methods are not locally Lipschitz continuous, meaning that extremely small perturbations in model input can yield large changes in explanations, a phenomenon which makes explanations appear inconsistent to a human observer. More recently, ref. 31 showed that post hoc methods based on the deep Taylor decomposition can be manipulated to produce arbitrary explanations. Such findings have led to calls to use simpler, explainable models when possible. 19
Intrinsically explainable models often have comparable predictive power to black box models, especially when constructed carefully. 19 This general observation has been demonstrated recently in a materials science context where interpretable (multi-)linear models were applied material property prediction problems and achieved accuracy close to state-of-the-art nonlinear approaches. 32 One of these model families was constructed by counting atomic n -grams present in a crystal lattice unit cell and assigning coefficients to their presence, inspired by the cluster expansion. Here we develop an analogous representation for organic molecules which we call the atom-induced molecular subgraph, or graphlet, representation, wherein a molecule is represented by constituent n -atom connected subgraphs. A similar representation was recently developed by ref. 9 and used to sample and characterize large chemical spaces of more than billions of molecules. 33–35 Here we show that such a representation can be combined with linear models for competitive and interpretable prediction.
We construct accurate, explainable linear models which, inspired by the many-body expansion, 36–38 approximate molecular properties as functions of molecular graphlets organized by their body-order, i.e. , the number of atoms in each graphlet. We show that so-constructed linear models perform competitively with nonlinear black box models across a variety of structure–property prediction tasks. We then show that this approach can naturally be used to produce coherent, additive explanations by projecting higher-order model coefficients onto atoms or bonds within their molecular context, and empirically find correlation between these projections and both chemical intuition and chemical theory. Finally, we examine how graphlet train and test statistics can be used to estimate distribution shift 39 and thereby quantify prediction uncertainty.
| Illustration of graphlet featurization and linear model construction (a) all induced subgraphs up to size 2 are counted in a set of 2 training molecules (b) form of a linear model fit to predict some molecular property from counts shown in (a). (c) The matrix formulation of (b). | ||
2.1 Graphlet fingerprint approach
Graphlet fingerprints, like other fingerprint approaches, are built upon pre-defined type labels assigned to the atoms and bonds in a molecular graph. We label nodes by atomic species, formal charge, and aromaticity. This implies that every node type has a precise degree which is constant across all instances in all molecular graphs. Edges are labeled according to bond type as either single, double, triple, or aromatic. As a result, the graphlet statistics form a typed version of D k degree statistics. 41 This rich typing scheme helps to capture information more efficiently at lower maximum graphlet size; as an example, with only species based typing an N + atom with 4 bonds is not distinguished from an N atom with 3 bonds until using a graphlet size of at least 5. Valence-based rich typing of atoms can resolve the difference between these atoms at a graphlet size of 1.
Graphlets are enumerated by a recursive algorithm similar to the explicit subgraph enumeration routine described in ref. 42 and 9 , during which we identify and count membership in isomorphism classes through our hashing technique described in the next section.
2.2 Graphlet fingerprint mathematical description
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
2.3 Hierarchical regression
| (6) |
| (7) |
| (8) |
Put less mathematically, using the graphlet approach, we can build a function up by first applying regression to the graphlet counts generated by atoms, and then to the graphlet counts generated by bonds, and then to the graphlet counts generated by connected triples, and so on, up to some graphlet size N , where the model at size n learns a correction to the model at size n – 1. This same hierarchical approach can be analogously applied to the other 2D graph fingerprints we examine. For path-based fingerprints, the hierarchical levels indexed by n correspond to the number of steps in the graph walks or, equivalently, the number of bonds. For circular fingerprints, the hierarchical levels n indicate the set of fragment features with radius equal to n .
2.4 Interpretation projections
| Illustration of interpretability scheme based on substructure graphs. A linear model associates some contribution to each fragment in the molecule. By tracking the inclusion relationships between subgraphs (red/blue arrows), we can create normalized matrices Ĝ and which can be used to move predictions between many-body levels. Of particular interest are interpretability projections to atoms, n = 1, and bonded pairs, n = 2. | ||
| (9) |
| (10) |
| (11) |
| (12) |
| ŷ = β·c . | (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
2.5 Uncertainty quantification and prediction adjustment based on unseen graphlets
We examine various methods of constructing uncertainty metrics based on unseen graphlets. While yet more approaches are possible, we explored using the total number of unseen graphlets, the fraction of unseen graphlets, and an auxiliary uncertainty regression model to weight the relative importance of unseen fragments of size s .
| ŷ = β·c + ·d | (22) |
2.6 Overview of data sources and experiments
2.7 implementation, 3.1 high accuracy on diverse chemical systems.
Overall, graphlet-based linear models show stronger performance than both nonlinear models and models constructed with other fingerprints, as seen in Fig. 3 which summarizes our QM9 experiments (additional learning curves including training performance are given in ESI Fig. S1 and S2 † ). First, considering hierarchical models, performance improves consistently with fragment size to a mean absolute error (MAE) of less than 5 kcal mol −1 for all models. The best of these models uses graphlet fingerprints and attains a test MAE of 1.74 kcal mol −1 . Although this is not quite the 1 kcal mol −1 widely considered to be chemical accuracy, 62 it is less than the error of the DFT used to calculate these values of Δ H at . 50 The RDKit fingerprint-based model follows this performance, with an MAE of 2.15 kcal mol −1 . The performance of these two fingerprint variants is likely similar because they capture similar chemical information, i.e. , atom-induced subgraphs vs. branched-path fingerprints which can be though of as edge-induced subgraphs. We hypothesize that the stronger performance of both graphlet and RDKit fingerprints over Morgan fingerprints is because they are a richer representation than the Morgan fingerprints, having many more features at a given size. We further hypothesize that the performance improvement of graphlet fingerprints over RDKit fingerprints is due to the relative redundancy present in RDKit fingerprints: because they are walk based, there are many RDKit fingerprint fragments corresponding to the same exact set of atoms for which there is necessarily only one graphlet.
| Test set performance vs. fragment count by model type, feature type, and hierarchicality on the QM9 ΔH task. The horizontal axis is shown in number of fragments rather than fingerprint size because the size parameter has different meanings across fingerprint types. The dashed horizontal line at 2.3 kcal mol indicates the accuracy of the DFT calculations that produced these ΔH values compared to experiment. The solid horizontal line at 1 kcal mol gives a common benchmark of “quantum chemical accuracy” at 1 kcal mol . The dotted horizontal line at 84.2 kcal mol shows the best MAE attained by fingerprint-based models in ref. . | ||
The nonlinear LightGBM models outperform linear models with small fragment counts, but this relationship is reversed as fragment count increases. This is possibly because LightGBM does not capture the additivity of fragment energies reflected in the many body expansion ansatz, which, by contrast, is well-captured by linear models. Instead of assigning an energy to each graphlet, the LightGBM model must examine a large set of features to sift through the combinations which produce good estimates of total energy. This hypothesis is consistent with the rapid increase in error of non-hierarchical LightGBM models with fragment count, which have to consider all fragments at once. Hierarchicality also eliminates feature correlation induced by the inclusion of smaller fragments within large ones, which may explain the trend of slightly better performance among the hierarchical models in general and the much stronger performance of LightGBM using the hierarchical approach.
3.2 Interpreting energy models on bonds
| Bond-level model interpretability: the projection of a ΔH model onto bonds along experimental bond dissociation energies (BDE) for ethane, ethene, and ethyne obtained from ref. . Energies are in units of kcal mol . | ||
| Relationship between Bond Dissociation Energies (BDEs) computed with DFT and the bond-level interpretations for a model fit to atomization energy on the QM9 dataset. | ||
| Bond | n | Pearson r |
|---|---|---|
| All | 24 | 0.4198 |
| C–H | 15 | 0.1414 |
| C–C | 4699 | 0.4968 |
| C–N | 1064 | 0.3043 |
| C–O | 1440 | 0.2266 |
| H–N | 990 | 0.2298 |
| H–O | 522 | −0.0584 |
3.3 Competitive performance for solubility prediction
Overall, we found that the graphlet fingerprints coupled with linear models predict small molecule solubility in four solvents competitively with nonlinear models from ref. 51 , which were trained on expensive DFT- and experiment-based features. Fig. 6 shows test RMSE (log molarity) for each model presented in ref. 51 and for graphlet-based linear and LightGBM models.
| Model performance on the solubility datasets from ref. . Root mean squared errors are in units of log molarity. Models from ref. are shown in shades of red in the left-hand side of each panel, models from this work are shown in shades of blue, offset on the right-hand side of each panel. | ||
Graphlet-fingerprint-based models are competitive on all datasets save for benzene, and are among the best for the water (wide) and water (wide-narrow) sets, while being both inexpensive and easy to interpret based on structural motifs (interpretations of solubility predictions are discussed in the following section, and shown in Fig. 7 ). Compared to nonlinear LightGBM models, linear models are unexpectedly strong on these tasks. This demonstrates that, surprisingly, our molecular representation coupled with linear models is useful outside the context of predicting extensive properties like energy.
| Linear model predictions of aqueous solubility projected to the atom level for selected backbones and functional groups. Colors show the contribution to the predicted log solubility (measured in molarity). Contributions of the functional groups to the overall solubility agree qualitatively with chemical intuition. | ||
We note again the relatively low expense of our approach compared to the models in ref. 51 ; because the latter models rely on features that involve DFT and experimental measurements, applying the model to an arbitrary new chemical can be limited by the speed to calculate, find, or measure these quantities. In contrast, a fingerprinting approach such as graphlet fingerprints can be applied to completely new molecules in timescales far less than a second. For these tasks, there are on the order of hundreds to thousands of graphlet features; precise counts are given in ESI Table S2. †
3.4 Atom-level interpretation of solubility models
3.5 admet leaderboards.
These tasks form an important and challenging collection of properties which are useful because candidate drugs must perform satisfactorily with respect to a host of variables apart from biochemical mechanism of the drug itself, but to Absorption, Distribution, Metabolism, Excretion, and Toxicity (ADMET) properties that characterize how the molecule interacts with important aspects of human biochemistry. In ESI Section S5 † we briefly overview the individual tasks addressed in this work; for details please see the TDC information.
Table 2 shows our performance compared to the existing leaderboard entries at the time of writing. A visualization of all of the models' performance for all leaderboard tasks is present in ESI Fig. S6 and S7. † Models using graphlet fingerprints score in the upper half of the leaderboard for seven out of nine of the tasks. Notably, all these high-scoring models used the LightGBM regressor; ridge regression did not perform impressively in these tests and was in the lower half of the leaderboard for five of the nine tasks. This is surprising in the context of ridge regression's strong performance on solubility prediction in Section 3.3, but less surprising in that we expect non-linear, non-extensive models to perform better on biological properties that may not be easy to represent linearly as a sum of all graphlet contributions.
| Task | LightGBM perf. | LightGBM rank | Ridge perf. | Ridge rank | Perf. metric |
|---|---|---|---|---|---|
| LD | 0.603 | 3/19 | 0.632 | 8/19 | MAE |
| AqSol | 0.803 | 5/16 | 1.105 | 15/16 | MAE |
| Lipo | 0.519 | 5/17 | 0.516 | 4/17 | MAE |
| PPBR | 8.729 | 6/17 | 10.699 | 15/17 | MAE |
| Caco2 | 0.316 | 7/19 | 0.306 | 6/19 | MAE |
| VDss | 0.500 | 8/17 | 0.448 | 13/17 | Spearman's ρ |
| Half life | 0.217 | 12/18 | 0.229 | 11/18 | Spearman's ρ |
| CL-Hepa | 0.341 | 13/16 | 0.349 | 12/16 | Spearman's ρ |
| CL-Micro | 0.525 | 14/18 | 0.600 | 4/18 | Spearman's ρ |
3.6 Exploiting interpretability to account for new information
| Performance improvement from adjustment based on unseen fragments. Both panels show the predicted and true atomization energies for every held-out fragment, coalesced into one figure. The upper panel shows the raw predictions and the lower shows the predictions after applying the adjustment. | ||
3.7 Uncertainty quantification
The explicit uncertainty model is a linear regression mapping the number of fragments of each size to the absolute residuals. This model is fit with non-negative least squares, guaranteeing non-negative residual prediction and giving coefficients with a natural interpretation as the contribution of a single unseen fragment of a given size to the model uncertainty in units of the regression target. The resulting model coefficients are given in ESI Table S3. †
| (23) |
Values of CC eff close to one occur in the best case when the CC approaches the oracle CC, values near zero occur when the UQ metric is no better than random guessing, and negative values occur when the UQ metric is worse than random assignment. In this way, we can think of CC eff as being related to the AUC in the same way that R 2 relates to MSE; a perfect CC eff is 1, an uninformative CC eff is 0.
All of the proposed measures of uncertainty based on unseen fragments have moderate to strong correlation with absolute residuals, shown in Fig. 9 . Confidence curves and CC eff values are shown in Fig. 10 . The fraction of unseen fragments performs the strongest under both correlation coefficients and our confidence curve efficiency metric.
| Correspondence of various metrics for uncertainty with error. (left) Number of unseen fragments in a test molecule, (center) fraction of unseen fragments in a test molecule, (right) calibrated UQ model which takes into account both the number of unseen graph fragments and their sizes. | ||
| Confidence curves comparing uncertainty metrics to an oracle. Each curve shows the expected error in the test dataset as a curve by systematically dropping tests points with the highest uncertainty values; lower curves are better. The “oracle” curve shows the error distribution when points are dropped in order of their error; this is the best possible confidence curve for this error distribution. | ||
4 Discussion
We contrast the straightforward interpretability of our approach with complications associated with applying post hoc interpretability methods to models built on molecular fingerprints, which can lead to inconsistencies and confusions. For example, some research 23,24 examines SHAP values on the subgraphs corresponding to fingerprint fragments. In this case, in addition to the inconsistency of SHAP discussed in ref. 30 , SHAP explanations can include contributions associated with the absence of a particular fragment, thereby explaining properties of molecules based on what they are not. This is reasonable from a statistical perspective, but cannot provide a mechanistic explanation in terms only of the contents of the molecular graph being examined; if an interpretability method entangles the molecule with the training dataset, the resulting interpretation can be unintuitive. By contrast, interpreting linear model coefficients instead focuses only on the fragments that are present in the given molecule and model coefficients for components that are not present are irrelevant to the prediction. We also note that care must be taken to always use unfolded fingerprints when attempting to explain model predictions, or else the one-to-many correspondence between features and molecular fragments 67–69 significantly complicates interpretation, if not rendering it fully impossible.
Still, even linear models with large numbers of coefficients can be difficult to interpret, motivating our projection interpretability scheme. In our graphlet models, the typical number of features can easily be in the thousands, and even up to a million features in the case of QM9 with large maximum fragment sizes. Also complicating interpretation of the model is the set of inclusion relationships between the fragments. To combat these issues, we used two techniques. First, we used a hierarchical fitting approach which aims to capture the largest amount of variation using the simplest graphlets, effectively attempting to impose a many-body hierarchy on the learned models. Second, we developed the interpretation projection technique to build atom, bond, or higher-body-order-graphlet level interpretations. We note that a similar interpretation method to our projection scheme is presented in ref. 70 , wherein the SHAP attributions of all of the fingerprint fragments containing a given atom are summed, giving an atom-level SHAP contribution; our projections could be considered to be a more general version of this technique. An advantage of our approach used with linear graphlet models is that it is additive in the sense of eqn (21) ; the explanation breaks the prediction into component parts which add to recapitulate the prediction. Additivity over the feature space is also guaranteed by SHAP, but because this includes the features which are absent from the molecule having nonzero SHAP values as described above, the projection of SHAP values onto atoms or bonds is not additive, that is, the projections do not add to the final prediction.
We also performed uncertainty quantification using the unseen graphlets types not present in training. Our approaches have some similarity to UQ metrics based on the distance of an unseen point to its nearest neighbor(s) in the training set, which have long been applied in molecular property prediction, including with fingerprints 71 and more recently with latent neural network representations. 72 However, our approach does not require comparison to the training dataset, thus scales to arbitrarily large datasets; the cost of evaluating the UQ metric does not increase with the training set size, which is desirable in general and especially in applications such as molecular screening which may require very many uncertainty evaluations.
Some similarity may be noted between our work and that of atom-in-molecule-ons (AMONs), 73 because each involves analysis of substructures. AMONs constitute a framework for the comparison of 3D configurations; in that lens, they are a composition of a selective (as opposed to exhaustive) fragmentation into subgraphs, and molecular similarity kernels. 74 3D information about target molecules is typically used for contexts where the target property varies with respect to the input coordinates-for example, conformational energy variations; the cheminformatics applications presented in this work are distinct because they do not depend on conformation.
We note some advantages of graphlet fingerprints over other fingerprints, some of which are noted in ref. 9 . Graphlet fingerprints may be considered at once more complete than Morgan-like fingerprints and more compact or less redundant than RDKit fingerprints. This is visible in the feature counts in Fig. 3 , also shown in the ESI, Table S1. † Due to the radial nature, many substructures have no direct representation in Morgan fingerprints. Notably, Morgan fingerprints cannot explicitly represent individual bonds, which important chemical and physical meanings. Thus, bond-level interpretations like those in 3.2 are impossible with Morgan fingerprints. Likewise, RDKit fingerprints cannot directly represent atoms: paths of length one-bonds are the smallest fragments in RDKit fingerprints. RDKit fingerprints are also redundant in their representation of fragments in individual molecules when multiple bond paths connect the same set of atoms. For example, in a molecule with a ring containing n atoms, there is precisely one graphlet-based fingerprint fragment containing exactly those atoms, yet RDKit fingerprints will produce n – 1 fingerprint elements containing that same set of atoms, each one missing one bond from the ring. This leads to many-to-one correspondence between model coefficients and atom subsets, which presents a challenge to directly interpreting these coefficients. This redundancy may also challenge machine learning methods, as the fingerprint vectors will be highly correlated, even when models are fit hierarchically by fragment size. Hierarchical fitting helps to alleviate this redundancy by assigning model contributions to the lowest fragment size possible.
Regarding computational efficiency, we note that Morgan fingerprints are less costly to compute on large molecules with large fragment sizes due to their highly restrictive radial fragment definition. Graphlet fingerprints scale similarly in cost with molecule and fragment size to RDKit fingerprints, though are slightly less costly due to the aforementioned lack of redundancy with respect to subsets of atoms. This is unsurprising, as RDKit fingerprints can be thought of as edge-induced subgraphs rather than node-induced subgraphs.
We note that identifying and counting graphlets has long shown promise in other application areas of machine learning. A kernel based on the number of shared graphlets between graphs has been used to predict functional residues of proteins. 75 Due to the potentially combinatoric cost of counting all graphlets on arbitrarily connected graphs, these methods often incorporate random sampling of small graphlets. 76 Examining the symmetry relationships between nodes within graphlets has been exploited to understand protein–protein interactions 77 and interactions between MicroRNA and small molecules. 78 Various spectral methods based on graphlets have been developed 79 and applied to problems such as biological network comparison. 80,81 Recently, graphlet substructure relationships have been used to improve performance of graph neural networks. 45
5 Conclusion
At the same time, we have shown that the transparent nature of fingerprint techniques comes with many additional advantages. For one, we show that hierarchical linear modeling in the graphlet approach, using a many-body expansion hypothesis, in some circumstances produces a more accurate model which is far more stable to the maximum graphlet size hyperparameter. We also show how graphlet inclusion relationships can be used to assign precise interpretations which decompose the model prediction across the input molecular structure. This was shown to produce reasonable correlation with chemical theory and chemical intuition in the case of both 2-body (bond) and 1-body (atom) projections. Finally, we showed how the interpretability of graphlet-fingerprint-based linear models provides natural methods for uncertainty quantification as well as model adjustments which address distribution shift, in particular, adjustments that estimate the effect of new topological structures arising in test molecules.
Future work could take on a variety of directions. For one, having shown comparable performance to methods from recent literature on a very wide array of tasks, the graphlet featurization approach is suitable for application to new chemical datasets. Methodologically, the uncertainty quantification and interpretability methods discussed in this work are but the tip of the iceberg; a variety of more complex schemes could be explored, and some of them might prove to produce better interpretations or more well-calibrated uncertainty estimates. We believe a comparison of the both the interpretability and UQ metrics presented here to others is warranted, along with evaluation of the UQ methods with other frequently used methods. 82 The problem of modeling uncertainty and constructing interpretations when using these features in combination with external features (such as ab initio properties) remains unsolved; in some sense, any feature that is itself a function of the molecular structure cannot present information that is orthogonal to the graphlet histogram, and so a method to project the information gained by models through these features back onto the molecular graph would need to be devised in order to extend the notions of interpretations presented here. In this work, we have concentrated on modeling data whose domain is scalar, that is, where the prediction target for each molecule is a single number. However, the graphlet distribution can be localized to their location in the graph, and so the graphlet technique could be modified to predict information such as the partial atomic charges within a molecule. Finally, the large number of graphlet types in a fingerprint (up to ≈10 6 in this work) points to the possibility of using intelligent strategies for pruning the set of features of interest. 83
Data availability
Conflicts of interest, acknowledgements.
- M. Hann and R. Green, Chemoinformatics — a new name for an old problem?, Curr. Opin. Chem. Biol. , 1999, 3 , 379–383 CrossRef CAS PubMed .
- P. Willett, Chemoinformatics: a history, Wiley Interdiscip. Rev.: Comput. Mol. Sci. , 2011, 1 , 46–56 CAS .
- T. Engel, Basic Overview of Chemoinformatics, J. Chem. Inf. Model. , 2006, 46 , 2267–2277 CrossRef CAS PubMed .
- L. C. Ray and R. A. Kirsch, Finding chemical records by digital computers, Science , 1957, 126 , 814–819 CrossRef CAS PubMed .
- Daylight Theory: Fingerprints – Screening and Similarity, https://www.daylight.com/dayhtml/doc/theory/theory.finger.html, accessed: 2023-10-03.
- G. Landrum, Fingerprints in the RDKit, https://www.rdkit.org/UGM/2012/Landrum_RDKit_UGM.Fingerprints.Final.pptx.pdf, accessed 4-Oct-2023.
- H. L. Morgan, The generation of a unique machine description for chemical structures-a technique developed at chemical abstracts service, J. Chem. Doc. , 1965, 5 , 107–113 CrossRef CAS .
- D. Rogers and M. Hahn, Extended-connectivity fingerprints, J. Chem. Inf. Model. , 2010, 50 , 742–754 CrossRef CAS PubMed .
- L. Bellmann, P. Penner and M. Rarey, Connected subgraph fingerprints: representing molecules using exhaustive subgraph enumeration, J. Chem. Inf. Model. , 2019, 59 , 4625–4635 CrossRef CAS PubMed .
- W. P. Walters and R. Barzilay, Applications of deep learning in molecule generation and molecular property prediction, Acc. Chem. Res. , 2020, 54 , 263–270 CrossRef PubMed .
- O. Wieder, S. Kohlbacher, M. Kuenemann, A. Garon, P. Ducrot, T. Seidel and T. Langer, A compact review of molecular property prediction with graph neural networks, Drug Discovery Today: Technol. , 2020, 37 , 1–12 CrossRef PubMed .
- Z. Li, M. Jiang, S. Wang and S. Zhang, Deep learning methods for molecular representation and property prediction, Drug Discov. Today , 2022, 103373 CrossRef PubMed .
- V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W.-k. Liao, A. Choudhary and A. Agrawal, Cross-property deep transfer learning framework for enhanced predictive analytics on small materials data, Nat. Commun. , 2021, 12 , 6595 CrossRef CAS PubMed .
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning, Nat. Commun. , 2019, 10 , 2903 CrossRef PubMed .
- F. H. Vermeire and W. H. Green, Transfer learning for solvation free energies: From quantum chemistry to experiments, Chem. Eng. J. , 2021, 418 , 129307 CrossRef CAS .
- Z. Wang, Z. Dai, B. Póczos and J. Carbonell, Characterizing and avoiding negative transfer, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition , 2019, pp. 11293–11302 Search PubMed .
- N. Hoffmann, J. Schmidt, S. Botti and M. A. Marques, Transfer learning on large datasets for the accurate prediction of material properties, Digital Discovery , 2023, 2 , 1368–1379 RSC .
- G. P. Wellawatte, H. A. Gandhi, A. Seshadri and A. D. White, A Perspective on Explanations of Molecular Prediction Models, J. Chem. Theory Comput. , 2023, 19 , 2149–2160 CrossRef CAS PubMed .
- C. Rudin, Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead, Nat. Mach. Intell. , 2019, 1 , 206–215 CrossRef PubMed .
- F. Oviedo, J. L. Ferres, T. Buonassisi and K. T. Butler, Interpretable and explainable machine learning for materials science and chemistry, Acc. Mater. Res. , 2022, 3 , 597–607 CrossRef CAS .
- M. T. Ribeiro, S. Singh and C. Guestrin, Why should i trust you?” Explaining the predictions of any classifier, Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining , 2016, pp. 1135–1144 Search PubMed .
- S. M. Lundberg and S.-I. Lee, A unified approach to interpreting model predictions, Adv. Neural Inf. Process. Syst. , 2017, 30 , 4768–4777 Search PubMed .
- F. O. Sanches-Neto, J. R. Dias-Silva, L. H. Keng Queiroz Junior and V. H. Carvalho-Silva, “py SiRC”: Machine Learning Combined with Molecular Fingerprints to Predict the Reaction Rate Constant of the Radical-Based Oxidation Processes of Aqueous Organic Contaminants, Environ. Sci. Technol. , 2021, 55 , 12437–12448 CrossRef CAS PubMed .
- Y. Ding, M. Chen, C. Guo, P. Zhang and J. Wang, Molecular fingerprint-based machine learning assisted QSAR model development for prediction of ionic liquid properties, J. Mol. Liq. , 2021, 326 , 115212 CrossRef CAS .
- M. Sundararajan, A. Taly and Q. Yan, Axiomatic attribution for deep networks, International conference on machine learning , 2017, pp. 3319–3328 Search PubMed .
- G. Montavon, S. Lapuschkin, A. Binder, W. Samek and K.-R. Müller, Explaining nonlinear classification decisions with deep taylor decomposition, Pattern Recogn. , 2017, 65 , 211–222 CrossRef .
- S. Ishida, K. Terayama, R. Kojima, K. Takasu and Y. Okuno, Prediction and interpretable visualization of retrosynthetic reactions using graph convolutional networks, J. Chem. Inf. Model. , 2019, 59 , 5026–5033 CrossRef CAS PubMed .
- A. Mastropietro, G. Pasculli, C. Feldmann, R. Rodríguez-Pérez and J. Bajorath, EdgeSHAPer: Bond-centric Shapley value-based explanation method for graph neural networks, Iscience , 2022, 25 , 105043 CrossRef PubMed .
- P. Xiong, T. Schnake, M. Gastegger, G. Montavon, K. R. Muller and S. Nakajima, Relevant Walk Search for Explaining Graph Neural Networks , 2023 Search PubMed .
- D. Alvarez-Melis and T. S. Jaakkola, On the robustness of interpretability methods, arXiv , 2018, preprint, arXiv:1806.08049, DOI: 10.48550/arXiv.1806.08049 .
- L. Sixt and T. Landgraf, A rigorous study of the deep taylor decomposition, Transactions on Machine Learning Research , 2022 Search PubMed .
- A. E. Allen and A. Tkatchenko, Machine learning of material properties: Predictive and interpretable multilinear models, Sci. Adv. , 2022, 8 , eabm7185 CrossRef CAS PubMed .
- L. Bellmann, P. Penner and M. Rarey, Topological similarity search in large combinatorial fragment spaces, J. Chem. Inf. Model. , 2020, 61 , 238–251 CrossRef PubMed .
- L. Bellmann, P. Penner, M. Gastreich and M. Rarey, Comparison of combinatorial fragment spaces and its application to ultralarge make-on-demand compound catalogs, J. Chem. Inf. Model. , 2022, 62 , 553–566 CrossRef CAS PubMed .
- L. Bellmann, R. Klein and M. Rarey, Calculating and optimizing physicochemical property distributions of large combinatorial fragment spaces, J. Chem. Inf. Model. , 2022, 62 , 2800–2810 CrossRef CAS PubMed .
- K. Yao, J. E. Herr and J. Parkhill, The many-body expansion combined with neural networks, J. Chem. Phys. , 2017, 146 , 014106 CrossRef PubMed .
- N. Lubbers, J. S. Smith and K. Barros, Hierarchical modeling of molecular energies using a deep neural network, J. Chem. Phys. , 2018, 148 , 241715 CrossRef PubMed .
- I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. Simm, R. Drautz, C. Ortner, B. Kozinsky and G. Csányi, The design space of E (3)-equivariant atom-centered interatomic potentials, arXiv , 2022, preprint, arXiv:2205.06643, DOI: 10.48550/arXiv.2205.06643 .
- J. Quinonero-Candela, M. Sugiyama, A. Schwaighofer and N. D. Lawrence, Dataset Shift in Machine Learning , Mit Press, 2008 Search PubMed .
- N. Pržulj, D. G. Corneil and I. Jurisica, Modeling interactome: scale-free or geometric?, Bioinformatics , 2004, 20 , 3508–3515 CrossRef PubMed .
- P. Mahadevan, D. Krioukov, K. Fall and A. Vahdat, Systematic topology analysis and generation using degree correlations, ACM SIGCOMM Computer Communication Review , 2006, vol. 36, pp. 135–146 Search PubMed .
- S. Wernicke, Efficient detection of network motifs, IEEE/ACM Transactions on Computational Biology and Bioinformatics , 2006, vol. 3, pp. 347–359 Search PubMed .
- S. Ulam, A collection of mathematical problems , Interscience Publishers, New York, 1960 Search PubMed .
- J. A. Bondy and R. L. Hemminger, Graph reconstruction—a survey, J. Graph Theor. , 1977, 1 , 227–268 CrossRef .
- G. Bouritsas, F. Frasca, S. Zafeiriou and M. M. Bronstein, Improving graph neural network expressivity via subgraph isomorphism counting, IEEE Trans. Pattern Anal. Mach. Intell. , 2022, 45 , 657–668 Search PubMed .
- B. Bollobás, Almost every graph has reconstruction number three, J. Graph Theor. , 1990, 14 , 1–4 CrossRef .
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, Less is more: Sampling chemical space with active learning, J. Chem. Phys. , 2018, 148 , 241733 CrossRef PubMed .
- K. Wang and A. W. Dowling, Bayesian optimization for chemical products and functional materials, Curr. Opin. Chem. Eng. , 2022, 36 , 100728 CrossRef .
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data , 2014, 1 , 1–7 Search PubMed .
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Von Lilienfeld, Prediction errors of molecular machine learning models lower than hybrid DFT error, J. Chem. Theor. Comput. , 2017, 13 , 5255–5264 CrossRef CAS PubMed .
- S. Boobier, D. R. Hose, A. J. Blacker and B. N. Nguyen, Machine learning with physicochemical relationships: solubility prediction in organic solvents and water, Nat. Commun. , 2020, 11 , 1–10 CrossRef PubMed .
- K. Huang, T. Fu, W. Gao, Y. Zhao, Y. Roohani, J. Leskovec, C. W. Coley, C. Xiao, J. Sun and M. Zitnik, Therapeutics data commons: Machine learning datasets and tasks for drug discovery and development , NeurIPS, 2021 Search PubMed .
- Therapeutics Data Commons: ADMET Leaderboards, https://tdcommons.ai/benchmark/admet_group/overview/, accessed: 2023-07-24.
- P. C. John, Y. Guan, Y. Kim, B. D. Etz, S. Kim and R. S. Paton, Quantum chemical calculations for over 200,000 organic radical species and 40,000 associated closed-shell molecules, Sci. Data , 2020, 7 , 244 CrossRef PubMed .
- G. Landrum, RDKit: Open-Source Cheminformatics. http://www.rdkit.org, accessed 2-Feb-2020.
- A. Hagberg, P. Swart and D. S Chult, Exploring network structure, dynamics, and function using NetworkX , 2008 Search PubMed .
- P. Virtanen, et al. , SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods , 2020, 17 , 261–272 CrossRef CAS PubMed .
- F. Pedregosa, et al. , Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res. , 2011, 12 , 2825–2830 Search PubMed .
- G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Lightgbm: A highly efficient gradient boosting decision tree, Adv. Neural Inf. Process. Syst. , 2017, 30 , 3149–3157 Search PubMed .
- C. Wang, Q. Wu, M. Weimer and E. Zhu, FLAML: A Fast and Lightweight AutoML Library , MLSys, 2021 Search PubMed .
- M. Tynes, W. Gao, D. J. Burrill, E. R. Batista, D. Perez, P. Yang and N. Lubbers, Pairwise difference regression: a machine learning meta-algorithm for improved prediction and uncertainty quantification in chemical search, J. Chem. Inf. Model. , 2021, 61 , 3846–3857 CrossRef CAS PubMed .
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Quantum chemical accuracy from density functional approximations via machine learning, Nat. Commun. , 2020, 11 , 5223 CrossRef CAS PubMed .
- S. J. Blanksby and G. B. Ellison, Bond dissociation energies of organic molecules, Acc. Chem. Res. , 2003, 36 , 255–263 CrossRef CAS PubMed .
- E. H. Simpson, The interpretation of interaction in contingency tables, J. Roy. Stat. Soc. , 1951, 13 , 238–241 CrossRef .
- G. Scalia, C. A. Grambow, B. Pernici, Y.-P. Li and W. H. Green, Evaluating Scalable Uncertainty Estimation Methods for Deep Learning-Based Molecular Property Prediction, J. Chem. Inf. Model. , 2020, 60 , 2697–2717 CrossRef CAS PubMed .
- X. Huang, J. Yang, L. Li, H. Deng, B. Ni and Y. Xu, Evaluating and Boosting Uncertainty Quantification in Classification, arXiv , 2019, preprint, arXiv:1909.06030, DOI: 10.48550/arXiv.1909.06030 .
- I. Cortés-Ciriano, Q. U. Ain, V. Subramanian, E. B. Lenselink, O. Méndez- Lucio, A. P. IJzerman, G. Wohlfahrt, P. Prusis, T. E. Malliavin and G. J. van Westen, others Polypharmacology modelling using proteochemometrics (PCM): recent methodological developments, applications to target families, and future prospects, MedChemComm , 2015, 6 , 24–50 RSC .
- I. Cortes-Ciriano, Bioalerts: a python library for the derivation of structural alerts from bioactivity and toxicity data sets, J. Cheminf. , 2016, 8 , 1–6 Search PubMed .
- D. S. Murrell, I. Cortes-Ciriano, G. J. Van Westen, I. P. Stott, A. Bender, T. E. Malliavin and R. C. Glen, Chemically Aware Model Builder (camb): an R package for property and bioactivity modelling of small molecules, J. Cheminf. , 2015, 7 , 1–10 Search PubMed .
- C. Humer, H. Heberle, F. Montanari, T. Wolf, F. Huber, R. Henderson, J. Heinrich and M. Streit, ChemInformatics Model Explorer (CIME): exploratory analysis of chemical model explanations, J. Cheminf. , 2022, 14 , 21 Search PubMed .
- R. P. Sheridan, B. P. Feuston, V. N. Maiorov and S. K. Kearsley, Similarity to molecules in the training set is a good discriminator for prediction accuracy in QSAR, J. Chem. Inf. Comput. Sci. , 2004, 44 , 1912–1928 CrossRef CAS PubMed .
- J. P. Janet, C. Duan, T. Yang, A. Nandy and H. J. Kulik, A quantitative uncertainty metric controls error in neural network-driven chemical discovery, Chem. Sci. , 2019, 10 , 7913–7922 RSC .
- B. Huang and O. A. von Lilienfeld, Quantum machine learning using atom-in-molecule-based fragments selected on the fly, Nat. Chem. , 2020, 12 , 945–951 CrossRef CAS PubMed .
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv. , 2017, 3 , e1603015 CrossRef PubMed .
- V. Vacic, L. M. Iakoucheva, S. Lonardi and P. Radivojac, Graphlet kernels for prediction of functional residues in protein structures, J. Comput. Biol. , 2010, 17 , 55–72 CrossRef CAS PubMed .
- N. Shervashidze, S. Vishwanathan, T. Petri, K. Mehlhorn and K. Borgwardt, Efficient graphlet kernels for large graph comparison, Artificial intelligence and statistics , 2009, pp. 488–495 Search PubMed .
- X.-D. Wang, J.-L. Huang, L. Yang, D.-Q. Wei, Y.-X. Qi and Z.-L. Jiang, Identification of human disease genes from interactome network using graphlet interaction, PLoS One , 2014, 9 , e86142 CrossRef PubMed .
- N.-N. Guan, Y.-Z. Sun, Z. Ming, J.-Q. Li and X. Chen, Prediction of potential small molecule-associated microRNAs using graphlet interaction, Front. Pharmacol. , 2018, 9 , 1152 CrossRef CAS PubMed .
- R. Kondor, N. Shervashidze and K. M. Borgwardt, The graphlet spectrum, Proceedings of the 26th Annual International Conference on Machine Learning , 2009, pp. 529–536 Search PubMed .
- N. Pržulj, Biological network comparison using graphlet degree distribution, Bioinformatics , 2007, 23 , e177–e183 CrossRef PubMed .
- S. F. Windels, N. Malod-Dognin and N. Pržulj, Graphlet Laplacians for topology-function and topology-disease relationships, Bioinformatics , 2019, 35 , 5226–5234 CrossRef CAS PubMed .
- M. H. Rasmussen, C. Duan, H. J. Kulik and J. H. Jensen, Uncertain of uncertainties? A comparison of uncertainty quantification metrics for chemical data sets, J. Cheminf. , 2023, 15 , 121 CAS .
- A. M. Krajewski, J. W. Siegel and Z.-K. Liu, Efficient Structure-Informed Featurization and Property Prediction of Ordered, Dilute, and Random Atomic Structures, arXiv , 2024, preprint, arXiv:2404.02849, DOI: 10.48550/arXiv.2404.02849 .
| † Electronic supplementary information (ESI) available. See DOI: |
| ‡ Current address: Analytics, Intelligence, and Technology Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. |
| § Current address: Department of Computer Science, The University of Chicago, Chicago, IL 60637, USA. |
scipy.optimize.linear_sum_assignment #
Solve the linear sum assignment problem.
The cost matrix of the bipartite graph.
Calculates a maximum weight matching if true.
An array of row indices and one of corresponding column indices giving the optimal assignment. The cost of the assignment can be computed as cost_matrix[row_ind, col_ind].sum() . The row indices will be sorted; in the case of a square cost matrix they will be equal to numpy.arange(cost_matrix.shape[0]) .
for sparse inputs
The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a ‘worker’) and vertex j of the second set (a ‘job’). The goal is to find a complete assignment of workers to jobs of minimal cost.
Formally, let X be a boolean matrix where \(X[i,j] = 1\) iff row i is assigned to column j. Then the optimal assignment has cost
where, in the case where the matrix X is square, each row is assigned to exactly one column, and each column to exactly one row.
This function can also solve a generalization of the classic assignment problem where the cost matrix is rectangular. If it has more rows than columns, then not every row needs to be assigned to a column, and vice versa.
This implementation is a modified Jonker-Volgenant algorithm with no initialization, described in ref. [2] .
New in version 0.17.0.
https://en.wikipedia.org/wiki/Assignment_problem
DF Crouse. On implementing 2D rectangular assignment algorithms. IEEE Transactions on Aerospace and Electronic Systems , 52(4):1679-1696, August 2016, DOI:10.1109/TAES.2016.140952
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Advertising & Talent Reach devs & technologists worldwide about your product, service or employer brand
- OverflowAI GenAI features for Teams
- OverflowAPI Train & fine-tune LLMs
- Labs The future of collective knowledge sharing
- About the company Visit the blog
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
No module named 'sklearn.utils.linear_assignment_'

- scikit-learn
- 5 Please re-read How to ask , as it would seem that you missed some crucial points the first time you read it, namely " DO NOT post images of code, data, error messages, etc. - copy or type the text into the question " (emphasis in the original). See why an image of your code is not helpful . – desertnaut Commented Jun 15, 2020 at 14:43
- 3 Additionally, this is a scikit-learn question, and it has nothing to do with deep-learning , yolo , or object-detection - kindly do not spam irrelevant tags (edited) – desertnaut Commented Jun 15, 2020 at 14:45
- I faced it when i going inside of deep learning and yolo . So how can i know exactly. – Furkan Eraslan Commented Jun 15, 2020 at 14:47
- 2 From the fact that you don't show anything related to these models/technlogies - just an import issue of a specific package. – desertnaut Commented Jun 15, 2020 at 14:48
5 Answers 5
The linear_assignment function is deprecated in 0.21 and will be removed from 0.23, but sklearn.utils.linear_assignment_ can be replaced by scipy.optimize.linear_sum_assignment .
You can use:
then you can run the file and don't need to change the code.
- 2 Note this point: stackoverflow.com/a/57992848/9328993 – Sajjad Aemmi Commented May 4, 2022 at 6:41
- 1 pip install scikit-learn==0.22.2 --upgrade --> might be useful for the ones who had installed the newer version before. – Koray Commented Dec 19, 2020 at 19:29
- Have faced with this issue with Deep Sort python implementation with scikit-learn 0.24 version, you saved my day. Thank you. – spawnfile Commented Jun 12, 2023 at 21:02
As yiakwy points out in a github comment the scipy.optimize.linear_sum_assignment is not the perfect replacement:
I am concerned that linear_sum_assignment is not equivalent to linear_assignment which later implements "maximum values" matching strategy not "complete matching" strategy, i.e. in tracking problem maybe an old landmark lost and a new detection coming in. We don't have to make a complete assignment, just match as more as possible.
I have found this out while trying to use it inside SORT-based yolo tracking code which that replacement broke (I was lucky that it did otherwise, I would get wrong results from the experiments without realising it...)
Instead, I suggest copying the module itself to the last version of sklearn and include as module in your code.
https://github.com/scikit-learn/scikit-learn/blob/0.22.X/sklearn/utils/linear_assignment_.py
For instance if you copy this file into an utils directory import with from utils.linear_assignment_ import linear_assignment
- Use pip to install lap and optionally scipy ;
- Uncomment the import and use the following function:
You are getting this error because you haven't install scikit module yet. Install scikit-learn module from https://pypi.org/project/scikit-learn/
- I did already. pip install -U scikit-learn Requirement already up-to-date: scikit-learn Requirement already satisfied, skipping upgrade: scipy Requirement already satisfied, skipping upgrade: joblib Requirement already satisfied, skipping upgrade: threadpoolctl Requirement already satisfied, skipping upgrade: numpy – Furkan Eraslan Commented Jun 15, 2020 at 14:45
- @FurkanEraslan There does not seem to be such a module in the current scikit-learn version: scikit-learn.org/stable/modules/… – desertnaut Commented Jun 15, 2020 at 15:11
Your Answer
Reminder: Answers generated by artificial intelligence tools are not allowed on Stack Overflow. Learn more
Sign up or log in
Post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged python scikit-learn or ask your own question .
- The Overflow Blog
- Mobile Observability: monitoring performance through cracked screens, old...
- Featured on Meta
- Announcing a change to the data-dump process
- Bringing clarity to status tag usage on meta sites
- What does a new user need in a homepage experience on Stack Overflow?
- Staging Ground Reviewer Motivation
- Feedback requested: How do you use tag hover descriptions for curating and do...
Hot Network Questions
- Is there a phrase for someone who's really bad at cooking?
- Causal Reconciliation: Is this a viable way for my FTL system to preserve the course of History?
- How can I get around 16 electrical receptacles in a small area with the least amount of wiring?
- How much new mathematics should we learn during the PhD? Are the courses we take during the PhD really important?
- Rings demanding identity in the categorical context
- Reconstruction of Riemann surface from a germ of holomorphic function
- Why is there no article after 'by'?
- How can moral disagreements be resolved when the conflicting parties are guided by fundamentally different value systems?
- A short story about a boy who was the son of a "normal" woman and a vaguely human denizen of the deep
- Took a pic of old school friend in the 80s who is now quite famous and written a huge selling memoir. Pic has ben used in book without permission
- Compact symmetric spaces and sub-root systems
- Why are complex coordinates outlawed in physics?
- Maximizing the common value of both sides of an equation
- In Top, *how* do conjugate homorphisms of groups induce homotopies of classifying maps?
- Cannot open and HTML file stored on RAM-disk with a browser
- How can judicial independence be jeopardised by politicians' criticism?
- Journal keeps messing with my proof
- Seinfeldisms in O.R
- Whence “uniform distribution”?
- Does someone know when GPT5 will be publicly available?
- Can IRS make the taxpayer pay the costs of litigation if the latter loses the case?
- Can you use 'sollen' the same way as 'should' in sentences about possibility that something happens?
- Who is the referent of "him" in Genesis 18:2?
- Duties when bringing Canadian goods to US in luggage

IMAGES
VIDEO
COMMENTS
The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C [i,j] is the cost of matching vertex i of the first partite set (a 'worker') and vertex j of the second set (a 'job'). The goal is to find a complete assignment of workers to ...
The linear_sum_assignment method doesn't support constraints or a custom objective, so I don't think this is possible.. However, you could formulate your problem as a mixed-integer linear programming problem (MILP) and solve it by means of PuLP 1.In order to evenly distribute the total costs per worker, you could minimize the difference between the maximum and the minimum total costs per worker.
The linear sum assignment problem is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C [i,j] is the cost of matching vertex i of the first partite set (a "worker") and vertex j of the second set (a "job"). The goal is to find a complete assignment of workers to jobs of ...
The program uses the linear assignment solver, a specialized solver for the assignment problem. The following code creates the solver. Note: The linear sum assignment solver only accepts integer values for the weights and values. The section Using a solver with non-integer data shows how to use the solver if your data contains non-integer values.
A Python module to solve the linear sum assignment problem (LSAP) efficiently. Extracted from SciPy, without significant modifications. This module is useful in cases when you need an efficient LSAP solver but you do not want to depend on the full SciPy library. Currently, the module depends on NumPy for array management.
4.5.4.4. scipy.optimize.linear_sum_assignment. Solve the linear sum assignment problem. The linear sum assignment problem is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C [i,j] is the cost of matching vertex i of the first partite set (a "worker") and vertex j of the ...
When trying to solve for assignments given a cost matrix, what is the difference between. using Scipy's linear_sum_assignment function (which I think uses the Hungarian method). describing the LP problem using a objective function with many boolean variables, add in the appropriate constraints and send it to a solver, such as through scipy.optimize.linprog?
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
The linear sum assignment problem is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C [i,j] is the cost of matching vertex i of the first partite set (a "worker") and vertex j of the second set (a "job"). The goal is to find a complete assignment of workers to jobs of ...
Purpose. The script benchmarks the performance of Python3 linear assignment problem solvers for random cost matrices of different sizes. These solvers are: lapjv.lapjv - a wrapper to a C++ implementation of Jonker-Volgenant algorithm re-written for Python 3 and optimized to take advantage of AVX2 instruction sets by Vadim Markovtsev at src {d}.
Linear assignment with non-perfect matching. Dec 8, 2020. The linear assignment problem (or simply assignment problem) is the problem of finding a matching between two sets that minimizes the sum of pair-wise assignment costs. This can be expressed as finding a matching (or independent edge set) in a bipartite graph G = (U, V, E) that minimizes ...
It will be great if there is a Python library with algorithm like that. Using the matrix scheme suggested by Mark, you could use the Jonker-Volgenant algorithm which is a modification of the Hungarian algorithm. It is implemented in scipy.optimize.linear_sum_assignment. Here is an example from the documentation, which you can modify to include ...
The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C [i,j] is the cost of matching vertex i of the first partite set (a 'worker') and vertex j of the second set (a 'job'). The goal is to find a complete assignment of workers to ...
In this step, we will solve the LP problem by calling solve () method. We can print the final value by using the following for loop. From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.
The logic is as follows: We reformulate the constrained problem into an equivalent unconstrained problem with a computationally intractable reward function, then we transform the unconstrained problem again using the tractable but conservative safety condition, and lastly, we run s-FEAST on the resulting problem and inherit standard convergence ...
The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C [i,j] is the cost of matching vertex i of the first partite set (a 'worker') and vertex j of the second set (a 'job'). The goal is to find a complete assignment of workers to ...
Put less mathematically, using the graphlet approach, we can build a function up by first applying regression to the graphlet counts generated by atoms, and then to the graphlet counts generated by bonds, and then to the graphlet counts generated by connected triples, and so on, up to some graphlet size N, where the model at size n learns a correction to the model at size n - 1.
I am trying to learn various implementations of the Hungarian Algorithm. Specifically, I want to maximise and get the highest score. I have found two solutions from various packages: (1) the munkres package, and (2) Linear Sum Assignment in Scipy
The linear sum assignment problem is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a 'worker') and vertex j of the second set (a 'job'). The goal is to find a complete assignment of workers to jobs of ...
The linear_assignment function is deprecated in 0.21 and will be removed from 0.23, but sklearn.utils.linear_assignment_ can be replaced by scipy.optimize.linear_sum_assignment. You can use: from scipy.optimize import linear_sum_assignment as linear_assignment. then you can run the file and don't need to change the code.