area problem solving questions gcse

Surface Area Questions

Surface Area of a Cuboid

Click here for Questions and Answers

Surface Area of a Prism

Surface Area of a Cylinder

Surface Area of a Sphere

Surface Area of a Cone

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

30 Problem Solving Maths Questions And Answers For GCSE

Sophie Bessemer

Problem solving maths questions can be challenging for GCSE students as there is no ‘one size fits all’ approach. In this article, we’ve compiled tips for problem solving, example questions, solutions and problem solving strategies for GCSE students. 

Since the current GCSE specification began, there have been many maths problem solving exam questions which take elements of different areas of maths and combine them to form new maths problems which haven’t been seen before. 

While learners can be taught to approach simply structured problems by following a process, questions often require students to make sense of lots of new information before they even move on to trying to solve the problem. This is where many learners get stuck.

GCSE MATHS 2025: STAY UP TO DATE Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2025. We’re analysing each paper during the course of the 2025 GCSEs in order to identify the key topic areas to focus on for your revision. GCSE dates 2025 GCSE results 2025 (when published) GCSE results 2024 Analysis of GCSE Maths Paper 1 (2024) Analysis of GCSE Maths Paper 2 (2024) Analysis of GCSE Maths Paper 3 (2024) Summary of ALL GCSE Maths Papers (2024)

How to teach problem solving

In the Ofsted maths review , published in May 2021, Ofsted set out their findings from the research literature regarding the sort of curriculum and teaching that best supports all pupils to make good progress in maths throughout their time in school.

Regarding the teaching of problem solving skills, these were their recommendations:

• Teachers could use a curricular approach that better engineers success in problem-solving by teaching the useful combinations of facts and methods, how to recognise the problem types and the deep structures that these strategies pair to.
• Strategies for problem-solving should be topic specific and can therefore be planned into the sequence of lessons as part of the wider curriculum. Pupils who are already confident with the foundational skills may benefit from a more generalised process involving identifying relationships and weighing up features of the problem to process the information. 
• Worked examples, careful questioning and constructing visual representations can help pupils to convert information embedded in a problem into mathematical notation.
• Open-ended problem solving tasks do not necessarily mean that the activity is the ‘ideal means of acquiring proficiency’. While enjoyable, open ended problem-solving activities may not necessarily lead to improved results.  

If you’re a KS2 teacher needing more support and CPD around teaching reasoning, problem solving & planning for depth we have a whole series of word problems and strategies to teach them available for you.

30 Problem Solving Maths Questions, Solutions & Strategies

Help your students prepare for their math GCSE with these free problem solving maths questions, solutions and strategies.

6 tips to tackling problem solving maths questions

There is no ‘one size fits all’ approach to successfully tackling problem solving maths questions however, here are 6 general tips for students facing a problem solving question:

• Read the whole question, underline important mathematical words, phrases or values.
• Annotate any diagrams, graphs or charts with any missing information that is easy to fill in.
• Think of what a sensible answer may look like. E.g. Will the angle be acute or obtuse? Is £30,000 likely to be the price of a coat?
• Tick off information as you use it.
• Draw extra diagrams if needed.
• Look at the final sentence of the question. Make sure you refer back to that at the end to ensure you have answered the question fully.

There are many online sources of mathematical puzzles and questions that can help learners improve their problem-solving skills. Websites such as NRICH and our blog on SSDD problems have some great examples of KS2, KS3 and KS4 mathematical problems.

Read more: KS2 problem solving and KS3 maths problem solving

In this article, we’ve focussed on GCSE questions and compiled 30 problem solving maths questions and solutions suitable for Foundation and Higher tier students. Additionally, we have provided problem solving strategies to support your students for some questions to encourage critical mathematical thinking . For the full set of questions, solutions and strategies in a printable format, please download our 30 Problem Solving Maths Questions, Solutions & Strategies.

Looking for additional support and resources at KS3? You are welcome to download any of the secondary maths resources from Third Space Learning’s resource library for free. There is a section devoted to GCSE maths revision with plenty of maths worksheets and GCSE maths questions . There are also maths tests for KS3, including a Year 7 maths test , a Year 8 maths test and a Year 9 maths test For children who need more support, our maths intervention programmes for KS3 achieve outstanding results through a personalised one to one tuition approach.

10 problem solving maths questions (Foundation tier)

These first 10 questions and solutions are similar to Foundation questions. For the first three, we’ve provided some additional strategies.

In our downloadable resource, you can find strategies for all 10 Foundation questions .

1) L-shape perimeter 

Here is a shape:

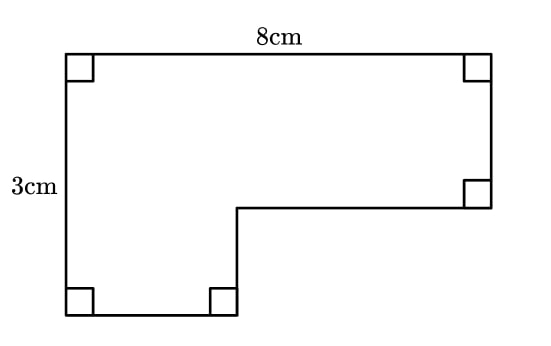
Sarah says, “There is not enough information to find the perimeter.”

Is she correct? What about finding the area?

• Try adding more information – giving some missing sides measurements that are valid. 
• Change these measurements to see if the answer changes.
• Imagine walking around the shape if the edges were paths. Could any of those paths be moved to another position but still give the same total distance?

The perimeter of the shape does not depend on the lengths of the unlabelled edges.

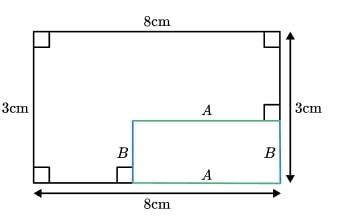
Edge A and edge B can be moved to form a rectangle, meaning the perimeter will be 22 cm. Therefore, Sarah is wrong.

The area, however, will depend on those missing side length measurements, so we would need more information to be able to calculate it.

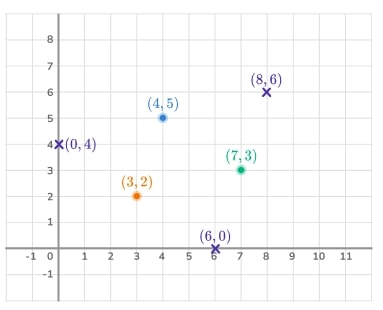
2) Find the missing point

Here is a coordinate grid with three points plotted. A fourth point is to be plotted to form a parallelogram. Find all possible coordinates of the fourth point.

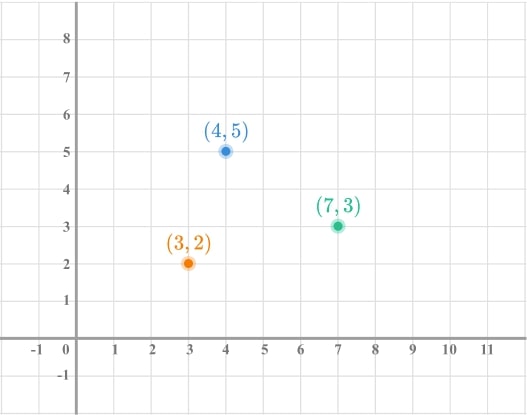
• What are the properties of a parallelogram?
• Can we count squares to see how we can get from one vertex of the parallelogram to another? Can we use this to find the fourth vertex?

There are 3 possible positions.

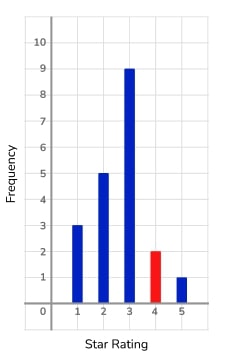
3) That rating was a bit mean!

The vertical line graph shows the ratings a product received on an online shopping website. The vertical line for 4 stars is missing.

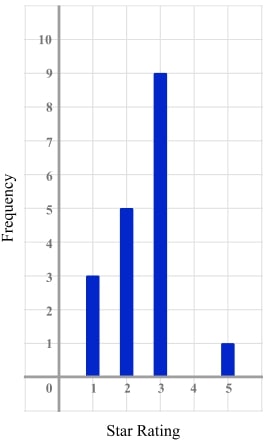
If the mean rating is 2.65, use the information to complete the vertical line graph.

Strategies 

• Can the information be put into a different format, either a list or a table?
• Would it help to give the missing frequency an algebraic label, x ?
• If we had the data in a frequency table, how would we calculate the mean?
• Is there an equation we could form?

Letting the frequency of 4 star ratings be x , we can form the equation \frac{45+4x}{18+x} =2.65

Giving x=2 

4) Changing angles

The diagram shows two angles around a point. The sum of the two angles around a point is 360°.

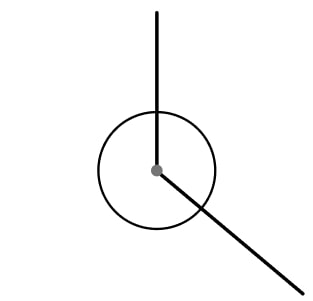
Peter says “If we increase the small angle by 10% and decrease the reflex angle by 10%, they will still add to 360°.”

Explain why Peter might be wrong.

Are there two angles where he would be correct?

Peter is wrong, for example, if the two angles are 40° and 320°, increasing 40° by 10% gives 44°, decreasing 320° by 10% gives 288°. These sum to 332°.

10% of the larger angle will be more than 10% of the smaller angle so the sum will only ever be 360° if the two original angles are the same, therefore, 180°.

5) Base and power

The integers 1, 2, 3, 4, 5, 6, 7, 8 and 9 can be used to fill in the boxes. 

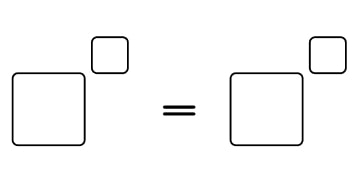
How many different solutions can be found so that no digit is used more than once?

There are 8 solutions.

6) Just an average problem 

Place six single digit numbers into the boxes to satisfy the rules.

The mean in maths is 5  \frac{1}{3}

The median is 5

The mode is 3.

How many different solutions are possible?

There are 4 solutions.

2, 3, 3, 7, 8, 9

3, 3, 4, 6, 7, 9

3, 3, 3, 7, 7, 9

3, 3, 3, 7, 8, 8

7) Square and rectangle  

The square has an area of 81 cm 2 . The rectangle has the same perimeter as the square.

Its length and width are in the ratio 2:1.

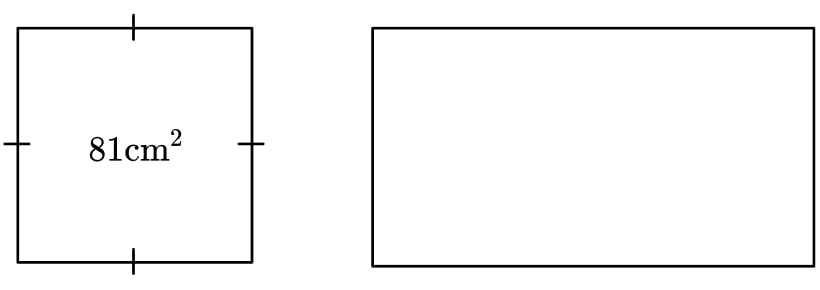
Find the area of the rectangle.

The sides of the square are 9 cm giving a perimeter of 36 cm. 

We can then either form an equation using a length 2x and width x . 

Or, we could use the fact that the length and width add to half of the perimeter and share 18 in the ratio 2:1. 

The length is 12 cm and the width is 6 cm, giving an area of 72 cm 2 .

8) It’s all prime

The sum of three prime numbers is equal to another prime number.

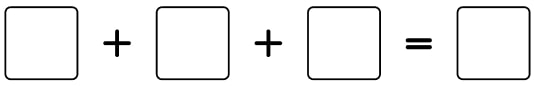
If the sum is less than 30, how many different solutions are possible?

There are 6 solutions. 

2 can never be used as it would force two more odd primes into the sum to make the total even.

9) Unequal share

Bob and Jane have £10 altogether. Jane has £1.60 more than Bob. Bob spends one third of his money. How much money have Bob and Jane now got in total?

Initially Bob has £4.20 and Jane has £5.80. Bob spends £1.40, meaning the total £10 has been reduced by £1.40, leaving £8.60 after the subtraction.

10) Somewhere between

Fred says, “An easy way to find any fraction which is between two other fractions is to just add the numerators and add the denominators.” Is Fred correct?

Solution 

Fred is correct. His method does work and can be shown algebraically which could be a good problem for higher tier learners to try.

If we use these two fractions \frac{3}{8} and \frac{5}{12} , Fred’s method gives us \frac{8}{20} = \frac{2}{5}

\frac{3}{8} = \frac{45}{120} , \frac{2}{5} = \frac{48}{120} , \frac{5}{12} = \frac{50}{120} . So \frac{3}{8} < \frac{2}{5} < \frac{5}{12}

10 problem solving maths questions (Foundation & Higher tier crossover)

The next 10 questions are crossover questions which could appear on both Foundation and Higher tier exam papers. We have provided solutions for each and, for the first three questions, problem solving strategies to support learners.

11) What’s the difference?

An arithmetic sequence has an nth term in the form an+b .

4 is in the sequence.

16 is in the sequence.

8 is not in the sequence.

-2 is the first term of the sequence.

What are the possible values of a and b ?

• We know that the first number in the sequence is -2 and 4 is in the sequence. Can we try making a sequence to fit? Would using a number line help?
• Try looking at the difference between the numbers we know are in the sequence.

If we try forming a sequence from the information, we get this:

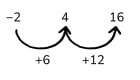
We can now try to fill in the missing numbers, making sure 8 is not in the sequence. Going up by 2 would give us 8, so that won’t work.

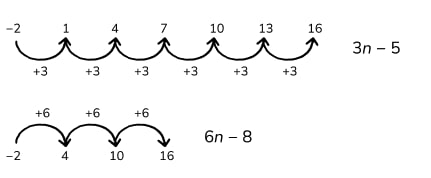
The only solutions are 6 n -8 and 3 n -5.

12) Equation of the hypotenuse

The diagram shows a straight line passing through the axes at point P and Q .

Q has coordinate (8, 0). M is the midpoint of PQ and MQ has a length of 5 units.

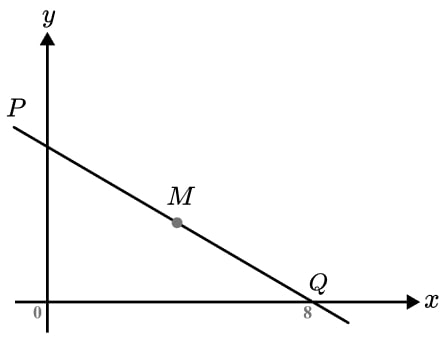
Find the equation of the line PQ .

• We know MQ is 5 units, what is PQ and OQ ?
• What type of triangle is OPQ ?
• Can we find OP if we know PQ and OQ ?
• A line has an equation in the form y=mx+c . How can we find m ? Do we already know c ?

PQ is 10 units. Using Pythagoras’ Theorem OP = 6

The gradient of the line will be \frac{-6}{8} = -\frac{3}{4} and P gives the intercept as 6.

13) What a waste

Harry wants to cut a sector of radius 30 cm from a piece of paper measuring 30 cm by 20 cm. 

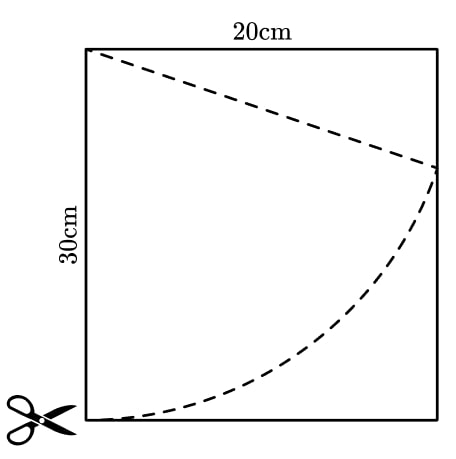
What percentage of the paper will be wasted?

• What information do we need to calculate the area of a sector? Do we have it all?
• Would drawing another line on the diagram help find the angle of the sector?

The angle of the sector can be found using right angle triangle trigonometry.

The angle is 41.81°.

This gives us the area of the sector as 328.37 cm 2 .

The area of the paper is 600 cm 2 .

The area of paper wasted would be 600 – 328.37 = 271.62 cm 2 .

The wasted area is 45.27% of the paper.

14) Tri-polygonometry

The diagram shows part of a regular polygon and a right angled triangle. ABC is a straight line. Find the sum of the interior angles of the polygon.

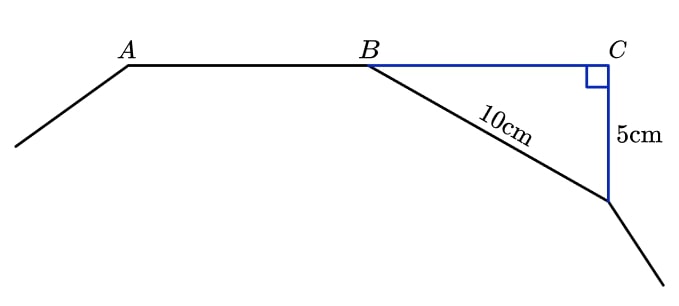
Finding the angle in the triangle at point B gives 30°. This is the exterior angle of the polygon. Dividing 360° by 30° tells us the polygon has 12 sides. Therefore, the sum of the interior angles is 1800°.

15) That’s a lot of Pi

A block of ready made pastry is a cuboid measuring 3 cm by 10 cm by 15 cm. 

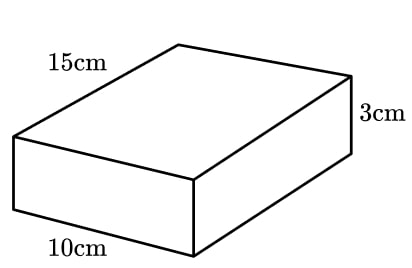
Anne is making 12 pies for a charity event. For each pie, she needs to cut a circle of pastry with a diameter of 18 cm from a sheet of pastry 0.5 cm thick.

How many blocks of pastry will Anne need to buy?

The volume of one block of pastry is 450 cm 3 . 

The volume of one cylinder of pastry is 127.23 cm 3 .

12 pies will require 1526.81 cm 3 .

Dividing the volume needed by 450 gives 3.39(…). 

Rounding this up tells us that 4 pastry blocks will be needed.

16) Is it right?

A triangle has sides of (x+4) cm, (2x+6) cm and (3x-2) cm. Its perimeter is 80 cm.

Show that the triangle is right angled and find its area.

Forming an equation gives 6x+8=80

This gives us x=12 and side lengths of 16 cm, 30 cm and 34 cm.

Using Pythagoras’ Theorem

16 2 +30 2 =1156 

Therefore, the triangle is right angled.

The area of the triangle is (16 x 30) ÷ 2 = 240 cm 2 .

17) Pie chart ratio

The pie chart shows sectors for red, blue and green. 

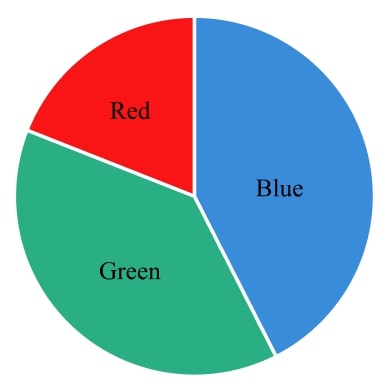
The ratio of the angles of the red sector to the blue sector is 2:7. 

The ratio of the angles of the red sector to the green sector is 1:3. 

Find the angles of each sector of the pie chart.

Multiplying the ratio of red : green by 2, it can be written as 2:6. 

Now the colour each ratio has in common, red, has equal parts in each ratio.

The ratio of red:blue is 2:7, this means red:blue:green = 2:7:6.

Sharing 360° in this ratio gives red:blue:green = 48°:168°:144°.

18) DIY Simultaneously

Mr Jones buys 5 tins of paint and 4 rolls of decorating tape. The total cost was £167.

The next day he returns 1 unused tin of paint and 1 unused roll of tape. The refund amount is exactly the amount needed to buy a fan heater that has been reduced by 10% in a sale. The fan heater normally costs £37.50.

Find the cost of 1 tin of paint.    

The sale price of the fan heater is £33.75. This gives the simultaneous equations

p+t = 33.75 and 5 p +4 t = 167.

We only need the price of a tin of paint so multiplying the first equation by 4 and then subtracting from the second equation gives p =32. Therefore, 1 tin of paint costs £32. 

19) Triathlon pace

Jodie is competing in a Triathlon. 

A triathlon consists of a 5 km swim, a 40 km cycle and a 10 km run. 

Jodie wants to complete the triathlon in 5 hours. 

She knows she can swim at an average speed of 2.5 km/h and cycle at an average speed of 25 km/h. There are also two transition stages, in between events, which normally take 4 minutes each.

What speed must Jodie average on the final run to finish the triathlon in 5 hours?

Dividing the distances by the average speeds for each section gives times of 2 hours for the swim and 1.6 hours for the cycle, 216 minutes in total. Adding 8 minutes for the transition stages gives 224 minutes. To complete the triathlon in 5 hours, that would be 300 minutes. 300 – 224 = 76 minutes. Jodie needs to complete her 10 km run in 76 minutes, or \frac{19}{15} hours. This gives an average speed of 7.89 km/h.

20) Indices

a 2x × a y =a 3

(a 3 ) x ÷ a 4y =a 32

Find x and y .

Forming the simultaneous equations

Solving these gives

10 problem solving maths questions (Higher tier)

This final set of 10 questions would appear on the Higher tier only. Here we have just provided the solutions. Try asking your learners to discuss their strategies for each question.  

21) Angles in a polygon

The diagram shows part of a regular polygon.

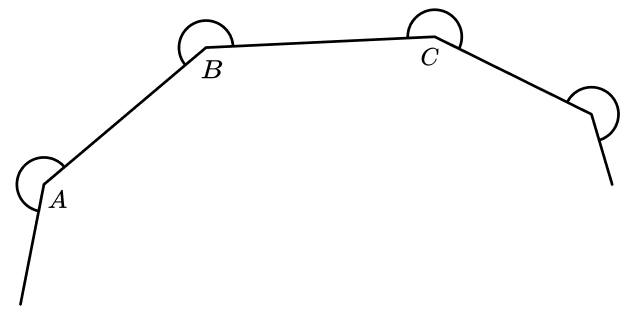
A , B and C are vertices of the polygon. 

The size of the reflex angle ABC is 360° minus the interior angle.

Show that the sum of all of these reflex angles of the polygon will be 720° more than the sum of its interior angles.

Each of the reflex angles is 180 degrees more than the exterior angle: 180 + \frac{360}{n}

The sum of all of these angles is n (180 + \frac{360}{n} ). 

This simplifies to 180 n + 360

The sum of the interior angles is 180( n – 2) = 180 n – 360

The difference is 180 n + 360 – (180 n -360) = 720°

22) Prism and force (Non-calculator)

The diagram shows a prism with an equilateral triangle cross-section.

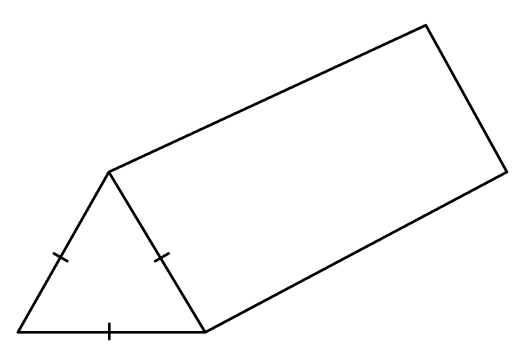
When the prism is placed so that its triangular face touches the surface, the prism applies a force of 12 Newtons resulting in a pressure of \frac{ \sqrt{3} }{4} N/m^{2}

Given that the prism has a volume of 384 m 3 , find the length of the prism.

Pressure = \frac{Force}{Area}

Area = 12÷ \frac{ \sqrt{3} }{4} = 16\sqrt{3} m 2

Therefore, the length of the prism is 384 ÷ 16\sqrt{3} = 8\sqrt{3} m

23) Geometric sequences (Non-calculator)

A geometric sequence has a third term of 6 and a sixth term of 14 \frac{2}{9}

Find the first term of the sequence.

The third term is ar 2 = 6

The sixth term is ar 5 = \frac{128}{9}

Diving these terms gives r 3 = \frac{64}{27}

Giving r = \frac{4}{3}

Dividing the third term twice by \frac{4}{3} gives the first term a = \frac{27}{8}

24) Printing factory

A printing factory is producing exam papers. When all 10 of its printers are working, it can produce all of the exam papers in 12 days.

For the first two days of printing, 3 of the printers are broken.

At the beginning of the third day it is discovered that 2 more printers have broken down, so the factory continues to print with the reduced amount of printers for 3 days. The broken printers are repaired and now all printers are available to print the remaining exams.

How many days in total does it take the factory to produce all of the exam papers?

If we assume one printer prints 1 exam paper per day, 10 printers would print 120 exam papers in 12 days. Listing the number printed each day for the first 5 days gives:

Day 5: 5 

This is a total of 29 exam papers.

91 exam papers are remaining with 10 printers now able to produce a total of 10 exam papers each day. 10 more days would be required to complete the job.

Therefore, 15 days in total are required.

25) Circles

The diagram shows a circle with equation x^{2}+{y}^{2}=13 .

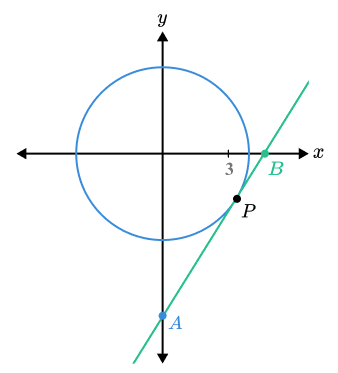
A tangent touches the circle at point P when x=3 and y is negative.

The tangent intercepts the coordinate axes at A and B .

Find the length AB .

Using the equation  x^{2}+y^{2}=13 to find the y value for P gives y=-2 .

The gradient of the radius at this point is - \frac{2}{3} , giving a tangent gradient of \frac{3}{2} .

Using the point (3,-2) in y = \frac {3}{2} x+c gives the equation of the tangent as y = \frac {3}{2} x – \frac{13}{2}

Substituting x=0 and y=0 gives A and B as (0 , -\frac {13}{2}) and ( \frac{13}{3} , 0)

Using Pythagoras’ Theorem gives the length of AB as ( \frac{ 13\sqrt{13} }{6} ) = 7.812.

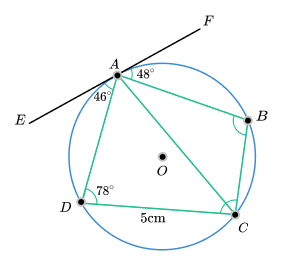
26) Circle theorems

The diagram shows a circle with centre O . Points A, B, C and D are on the circumference of the circle. 

EF is a tangent to the circle at A . 

Angle EAD = 46°

Angle FAB = 48°

Angle ADC = 78°

Find the area of ABCD to the nearest integer.

The Alternate Segment Theorem gives angle ACD as 46° and angle ACB as 48°.

Opposite angles in a cyclic quadrilateral summing to 180° gives angle ABC as 102°.

Using the sine rule to find AC will give a length of 5.899. Using the sine rule again to find BC will give a length of 3.016cm.

We can now use the area of a triangle formula to find the area of both triangles.

0.5 × 5 × 5.899 × sin (46) + 0.5 × 3.016 × 5.899 × sin (48) = 17 units 2 (to the nearest integer).

27) Quadratic function

The quadratic function f(x) = -2x^{2} + 8x +11 has a turning point at P .

Find the coordinate of the turning point after the transformation -f(x-3) .

There are two methods that could be used. We could apply the transformation to the function and then complete the square, or, we could complete the square and then apply the transformation.

Here we will do the latter.

This gives a turning point for f(x) as (2,19).

Applying -f(x-3) gives the new turning point as (5,-19).

28) Probability with fruit

A fruit bowl contains only 5 grapes and n strawberries.

A fruit is taken, eaten and then another is selected.

The probability of taking two strawberries is \frac{7}{22} .

Find the probability of taking one of each fruit. 

There are n+5 fruits altogether.

P(Strawberry then strawberry)= \frac{n}{n+5} × \frac{n-1}{n+4} = \frac{7}{22}

This gives the quadratic equation 15n^{2} - 85n - 140 = 0

This can be divided through by 5 to give 3n^{2} - 17n- 28 = 0

This factorises to (n-7)(3n + 4) = 0

n must be positive so n = 7.

The probability of taking one of each fruit is therefore, \frac{5}{12} × \frac{7}{11} + \frac {7}{12} × \frac {5}{11} = \frac {70}{132}

29) Ice cream tub volume

An ice cream tub in the shape of a prism with a trapezium cross-section has the dimensions shown. These measurements are accurate to the nearest cm.

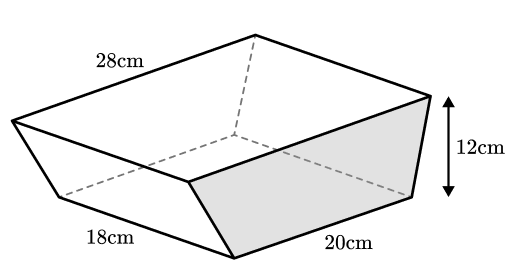
An ice cream scoop has a diameter of 4.5 cm to the nearest millimetre and will be used to scoop out spheres of ice cream from the tub.

Using bounds find a suitable approximation to the number of ice cream scoops that can be removed from a tub that is full.

We need to find the upper and lower bounds of the two volumes. 

Upper bound tub volume = 5665.625 cm 3

Lower bound tub volume = 4729.375 cm 3

Upper bound scoop volume = 49.32 cm 3  

Lower bound scoop volume = 46.14 cm 3  

We can divide the upper bound of the ice cream tub by the lower bound of the scoop to get the maximum possible number of scoops. 

Maximum number of scoops = 122.79

Then divide the lower bound of the ice cream tub by the upper bound of the scoop to get the minimum possible number of scoops.

Minimum number of scoops  = 95.89

These both round to 100 to 1 significant figure, Therefore, 100 scoops is a suitable approximation the the number of scoops.

30) Translating graphs

 The diagram shows the graph of y = a+tan(x-b ).

The graph goes through the points (75, 3) and Q (60, q).

Find exact values of a , b and q .

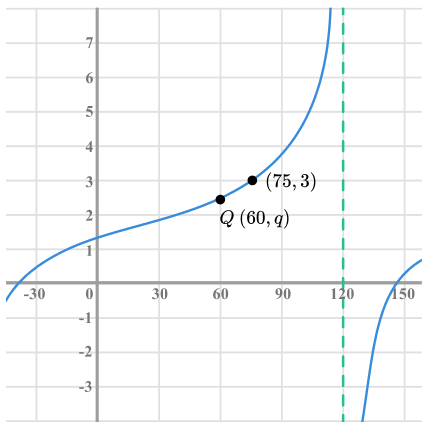
The asymptote has been translated to the right by 30°. 

Therefore, b=30

So the point (45,1) has been translated to the point (75,3). 

Therefore, a=2

We hope these problem solving maths questions will support your GCSE teaching. To get all the solutions and strategies in a printable form, please download the complete resource .

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 169,000 primary and secondary students become more confident, able mathematicians.

Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview

• 5,000+ Topicwise Questions & Answers Included
• Best for 11+ Grammar & Independent School Exams
• Improve Speed, Accuracy & Time Management

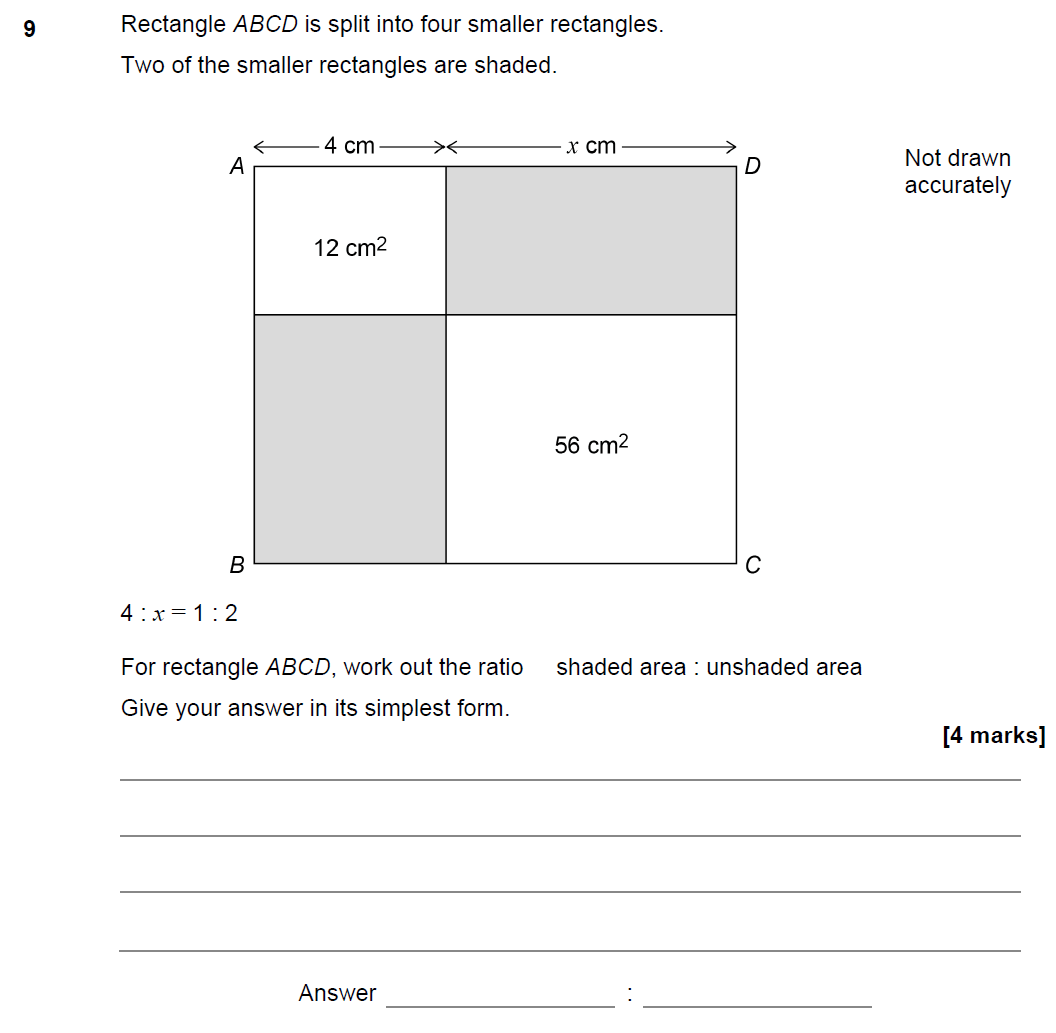
GCSE Area and Perimeter Questions and Answers

These detailed solutions are visible only for premium members

Please register to unlock over 135+ GCSE Maths Solved Past & Predicted Papers. 5,000+ Topicwise Questions with Step by Step Solutions

GCSE Topics

• Algebraic Expressions (190)
• Factorizing Expressions (14)
• Parallel and Perpendicular Lines (36)
• Function Machine (20)
• Algebraic Formulae (20)
• Simplifying Expressions (128)
• Quadratic Graphs (51)
• Collecting like Terms (50)
• Linear Inequalities (48)
• Turning Points (22)
• Indices (112)
• Quadratic Inequalities (10)
• Sketching Graphs (67)
• Order of Operations (BIDMAS) (16)
• Laws of Indices (70)
• Fractional Indices (28)
• Sequences (74)
• Exponential Graphs (16)
• Cubic Equations (18)
• Algebraic Indices (16)
• Arithmetic Sequences (43)
• Gradients of Curves (13)
• Rates of Change (5)
• Negative Indices (16)
• Quadratic Sequences (19)
• Factorizing Quadratics (11)
• Formulae (3)
• Algebraic Fractions (23)
• Coordinates (101)
• Cubic and Reciprocal Graphs (19)
• Linear Equations (190)
• Gradient of a line (67)
• Transforming Graphs (8)
• Simultaneous Equations (42)
• Equations of Straight Lines (91)
• Areas under curves (17)
• Geometric Sequences (11)
• Quadratics and Fractions (1)
• Quadratic Equations (104)
• Straight Line Graphs (74)
• Algebraic Proof (39)
• Algebraic Equations (308)
• Writing Formulae (1)
• Quadratic Formula (22)
• Real-life Graphs (14)
• Function Notation (26)
• Completing the Square (11)
• Trigonometric Graphs (18)
• Inverse Functions (14)
• Factorising Expressions (30)
• Substitution (59)
• Graphs of inequalities (12)
• Equation of a Circle (22)
• Composite Functions (14)
• Factorising Quadratics (27)
• Speed Distance Time (74)
• Velocity-time Graphs (18)
• Iterative Methods (16)
• Time Tables (4)
• Expanding Brackets (61)
• Expanding Double Brackets (4)
• Rearranging Formulae (40)
• Ratio & Proportion (248)
• Compound Measures (26)
• Proportion and Graphs (12)
• Unit Conversions (84)
• Growth and Decay (9)
• Density (24)
• Direct and Inverse Proportion (62)
• Scale diagrams and maps (17)
• 3D Shapes (74)
• Translations (25)
• Parallel Lines (22)
• Rotational Symmetry (9)
• Volume & Surface Area (87)
• Enlargement (27)
• Triangles (189)
• Similar Shapes (34)
• Squares (41)
• Congruent Triangles (27)
• Symmetry (18)
• Rectangles (68)
• Bearings (19)
• Line Symmetry (14)
• Nets of solids (2)
• Parallelograms (23)
• Trigonometry Lengths (73)
• Unit Conversion (2)
• Angles (135)
• Rhombus (7)
• Trigonometry Angles (98)
• 3D trigonometry (6)
• Pythagoras Theorem (45)
• Trapeziums (31)
• Sine Rule (21)
• Circles (1)
• 3D Pythagoras Theorem (8)
• Prisms (23)
• Cosine Rule (19)
• Constructing Perpendicular Lines (11)
• Circles, Sectors and Arcs (110)
• Vectors (55)
• Constructions (32)
• Cylinders (17)
• Plans and Elevations (15)
• Circle Theorems (33)
• Scale Drawings and Maps (26)
• Transformations (54)
• Reflection (30)
• Polygons (39)
• Pyramid (12)
• Area and Perimeter (179)
• Rotations (25)
• Scale Factor (39)
• Box plots (18)
• Scatter graphs (28)
• Time series graphs (14)
• Averages and Range (33)
• Sampling (2)
• Line Graphs (14)
• Frequency Table (50)
• Cumulative Frequency (29)
• Mean, mode and Median (94)
• Comparing Data (16)
• Stem and Leaf Diagrams (4)
• Data and Sampling (13)
• Histograms (23)
• Bar charts (29)
• Pictograms (14)
• Pie charts (26)
• Frequency Polygon (6)
• Conditional Probability (13)
• Independent Events (14)
• interpreting via collected data and calculated probabilitites (1)
• Comparing Probabilities (1)
• Probability (2)
• Sample space diagram (20)
• AND & OR Rules (56)
• Two way Tables (7)
• Relative Frequency (24)
• Tree diagrams (38)
• Frequency and Outcomes (12)
• Venn Diagrams (42)
• Set Notation (11)
• Geometric Mean (1)
• Arithmetic Mean (1)
• Comparing Statistical Measures (1)
• Factors, Multiples and Primes (88)
• Equivalent Fractions (16)
• Fractions of amounts (15)
• Simple and Compound Interest (36)
• Division (1)
• Fractions to decimals (29)
• Multipliers (21)
• Addition and Subtraction (57)
• Multiplication (1)
• Fractions to percentages (12)
• Fraction problems (22)
• Arithmetic Word Problems (182)
• Percentages (222)
• Ordering Numbers, (18)
• Decimals to Fractions (23)
• Rounding Numbers (87)
• Reverse Percentages (13)
• Odd and Even Numbers (28)
• Estimation (80)
• Decimals to Percentages (6)
• Multiplication and Division (96)
• Percentage Change (56)
• lcm word problems (11)
• Laws of Indices (16)
• Significant Figures (77)
• Order of Operations (13)
• HCF Word Problems (2)
• Profit and Loss (1)
• Decimals (137)
• Percentage Profit and Loss (21)
• Square Roots (41)
• Decimal Places (77)
• Ordering Fractions (5)
• Recurring Decimals (19)
• Repeated Percentage Change (11)
• Rounding Numbers, Estimation, Significant Figures, Decimal Places (14)
• Percentage to Fractions (8)
• Multiplying Decimals (19)
• Calculator Skills (50)
• Product Rule (11)
• Place Value (11)
• Dividing Decimals (27)
• Standard form (48)
• Error Intervals (26)
• Cube Roots (14)
• Pecentage Change (8)
• Ordering Decimals (8)
• Counting Strategies (24)
• Negative Numbers (14)
• Fractions (173)
• Square Numbers (48)
• Upper and Lower Bounds (25)
• Mixed Numbers (27)
• Cube Numbers (30)
• Limits of Accuracy (20)
• Operations with fractions (41)
• HCF, LCM (34)
• Comparing Numbers (24)
• Interpreting and Comparing Data (1)
• Scatter Graph (1)
• Time Series Graphs (1)

The main topics in GCSE Maths are:

• Ratio, Proportion and Rates of Change 
• Geometry and Measures
• Statistics 
• Probability 
• Statistical Measures 
• Data Visualisation 

With regular practice of GCSE Maths topic-wise questions and GCSE Maths past pacers , you can easily score high marks.

Although many people think of GCSE maths as a difficult subject, with the correct training and preparation,you can master it in time. You can practice GCSE Maths  topic-wise questions daily to improve speed, accuracy, and time and to score high marks in the GCSE Maths exam.

A grade of 4 or 5 would be considered "good" because the government has established a 4 as the passing grade; a grade of 5 is seen as a strong pass. Therefore, anything that exceeds this level would be considered good. You can practice GCSE Maths topic-wise questions to score good grades in the GCSE Maths exam.

You can get a high score in GCSE Maths through meticulous practice of GCSE Maths topic-wise questions and GCSE Maths past papers .

Subscribe to Newsletter

** Get 10% off coupon code on your first order, valid sitewide.

PiAcademy Partners

Follow us on

More than 20,000 registered members!

Exam papers.

© 2014 - 2024 PiAcademy Limited, All Rights Reserved

The resources on this page will hopefully help you teach AO2 and AO3 of the new GCSE specification - problem solving and reasoning.

This brief lesson is designed to lead students into thinking about how to solve mathematical problems. It features ideas of strategies to use, clear steps to follow and plenty of opportunities for discussion.

The PixiMaths problem solving booklets are aimed at "crossover" marks (questions that will be on both higher and foundation) so will be accessed by most students. The booklets are collated Edexcel exam questions; you may well recognise them from elsewhere. Each booklet has 70 marks worth of questions and will probably last two lessons, including time to go through answers with your students. There is one for each area of the new GCSE specification and they are designed to complement the PixiMaths year 11 SOL.

These problem solving starter packs are great to support students with problem solving skills. I've used them this year for two out of four lessons each week, then used Numeracy Ninjas as starters for the other two lessons.  When I first introduced the booklets, I encouraged my students to use scaffolds like those mentioned here , then gradually weaned them off the scaffolds. I give students some time to work independently, then time to discuss with their peers, then we go through it as a class. The levels correspond very roughly to the new GCSE grades.

Some of my favourite websites have plenty of other excellent resources to support you and your students in these assessment objectives.

@TessMaths has written some great stuff for BBC Bitesize.

There are some intersting though-provoking problems at Open Middle.

I'm sure you've seen it before, but if not, check it out now! Nrich is where it's at if your want to provide enrichment and problem solving in your lessons.

MathsBot  by @StudyMaths has everything, and if you scroll to the bottom of the homepage you'll find puzzles and problem solving too.

I may be a little biased because I love Edexcel, but these question packs are really useful.

The UKMT has a mentoring scheme that provides fantastic problem solving resources , all complete with answers.

I have only recently been shown Maths Problem Solving and it is awesome - there are links to problem solving resources for all areas of maths, as well as plenty of general problem solving too. Definitely worth exploring!

• International
• Education Jobs
• Schools directory
• Resources Education Jobs Schools directory News Search

GCSE Practice Exam Questions - Length, Area and Volume.

Subject: Whole school

Age range: 14-16

Resource type: Assessment and revision

Last updated

21 March 2021

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

This is a worksheet with some practice GCSE questions I have compiled from past test papers and GCSE textbooks. The questions range from a Grade C to a Grade A.

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

Empty reply does not make any sense for the end user

bellachan001

Excellent !!! But how to check the answer ?

A great set of questions which build up nicely in difficulty. This task would be great for ay higher student to see the progression needed to complete questions on area, length and volume.

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• Go to Dashboard
• My Children
• Childrens' Scores
• Student Scores
• Tutee Scores
• Games & Quizzes
• Code Breakers
• Topic Review Sheets
• KS2 SATS Questions
• GCSE Questions by Topic
• Past Paper Solutions
• User Guides

PMT Education is looking for a full-time Customer Support Specialist

Get £10 off your first lesson on PMT Tuition using the code PMTSEPT10

Edexcel Algebra Questions by Topic

Swansea University - PhD Physics

Early career researcher and established Physicist. Experienced tutor of 5 years privately and in schools.

On this page you can find past paper questions separated by topic and topic tests, for both Foundation and Higher tiers. All question sets are taken from past papers, except for the third set, which features topic tests. Set 5 includes the latest past paper questions from 2021 to 2023. Set 4 is from 2017-2021 and is the only set with video solutions .

It is recommended to start with Set 4 and Set 5, and if you need additional practice, you can work on sets 1-3 afterwards.

For notes, worksheets and their solutions, visit the GCSE Algebra Revision page. Full past papers and model solutions can be found on the Paper 1 , Paper 2 and Paper 3 pages.

Notation Vocabulary and Manipulation

• Algebraic Proofs (FH)
• Deriving Expressions (F)
• Deriving Expressions (FH)
• Expanding Equations (F)
• Expanding Expressions (FH)
• Factorising Equations (F)
• Factorising Expressions (FH)
• Forming Equations (F)
• Forming Equations (FH)
• Input-Output (F)
• Manipulation of Formulae (F)
• Manipulation of Formulae (FH)
• Simplifying Expressions (F)
• Simplifying Expressions (FH)
• Solving Using Indices (FH)
• Substitution (F)
• Substitution Into Equations (FH)
• Sequence of Diagrams (FH)
• Sequence of Numbers (FH)
• Sequences of Diagrams (F)
• Sequences of Numbers (F)
• Conversion Graphs (F)
• Conversion Graphs (FH)
• Coordinates in 3D (FH)
• Distance-Time Graphs (F)
• Distance-Time Graphs (FH)
• Exponential Growth and Decay (FH)
• Gradients of Straight Lines (FH)
• Graphs of Circles (FH)
• Graphs of Linear Equations (FH)
• Graphs of Quadratic Equations (FH)
• Graphs of Trigonometrical Functions (FH)
• Line Graphs (F)
• Line Graphs of Real Situations (FH)
• Transformation of Graphs (FH)
• Using y=mx+c (FH)

Solving Equations and Inequalities

• Solving Inequalities (F)
• Solving Inequalities (FH)
• Solving Linear Equations (F)
• Solving Linear Equations (FH)
• Solving Quadratic Equations (F)
• Solving Quadratic Equations (FH)
• Solving by Trial and Improvement (FH)
• Algebraic Proofs (H)
• Expanding Equations (H)
• Factorising Expressions (H)
• Forming Equations (H)
• Manipulation of Formulae (H)
• Simplifying Expressions (H)
• Solving Algebraic Fraction Equations (H)
• Solving Algebraic Fractions (H)
• Solving Using Indices (H)
• Substitution (H)
• Exponential Growth and Decay (H)
• Gradients of Straight Lines (H)
• Graphs of Circles (H)
• Graphs of Linear Equations (H)
• Graphs of Quadratic Equations (H)
• Graphs of Trigonometrical Functions (H)
• Line Graphs of Real Situations (H)
• Transformation of Graphs (H)
• Using y=mx+c (H)
• Solving Inequalities (H)
• Solving Simultaneous Equations (H)
• Expanding Expressions (F)
• Simplfying Equations (FH) 2
• Simplifying Equations (F)
• Simplifying Equations (FH) 1
• Substituting Into Equations (F)
• Substituting Into Equations (FH)
• Sequences (F)
• Sequences (FH)
• Distance-Time and Travel Graphs (F)
• Distance-Time and Travel Graphs (FH)
• Graphs of Linear Equations (F)
• Solving Simultaneous Equations (FH)
• Trial and Improvement (FH)
• Deriving Expressions (H)
• Expanding Expressions (H)
• Functions (H)
• Simplfying Equations (H) 2
• Simplifying Equations (H) 1
• Substituting Into Equations (H)
• Sequences (H)
• Graphs of Cubic Equations (H)
• Graphs of Reciprocal Equations (H)
• Transformation of Functions (H)
• Solving Linear Equations (H)
• Complex Graphs and Simultaneous Equations (F)
• Equations and Inequalities (F)
• Manipulating Expressions (F)
• Quadratic Equations and Graphs (F)
• Real-Life and Algebraic Linear Graphs (F)
• Algebra (H)
• Direct and Indirect Proportion (H)
• Direct and Inverse Proportion and Compound Measures (H)
• Graphs and Coordinate Geometry (H)
• Manipulating Expressions (H)
• Quadratic, Cubic and Other Graphs (H)
• Quadratics and Complex Graphs (H)
• Quadratics, Inequalities and Simultaneous Equations (H)

Notation, Vocabulary and Manipulation

• Inputs and Outputs (F)
• Substitution into Equations (F)
• Coordinates (F)
• Cubic and Reciprocal Graphs (F)
• Equations of Straight Lines (F)
• Graphs of Quadratic Equations (F)
• Interpreting Gradients (F)
• Simultaneous Equations (F)
• Solving Quadratic Equations(F)
• Algebraic Fractions (H)
• Algebraic Proof (H)
• Expanding Triple Brackets (H)
• Factorising Equations (H)
• Functions (Composite or Inverse) (H)
• Substitution into Equations (H)
• Geometric Progression (H)
• Circle Equations and Tangents (H)
• Coordinates (H)
• Cubic and Reciprocal Graphs (H)
• Distance-Time Graphs (H)
• Equations of Straight Lines (H)
• Exponential and Trigonometric Graphs (H)
• Interpreting Gradients (H)
• Parallel or Perpendicular Lines (H)
• Simultaneous Equations on Graphs (H)
• Translations and Reflections of Functions (H)
• Velocity-Time Graphs (H)
• Completing the Square (H)
• Inequalities (H)
• Inequalities on Graphs (H)
• Iteration (H)
• Quadratic Sequences (H)
• Simultaneous Equations (H)
• Solve by Factorising (H)
• Solving Quadratic Equations (H)

Notation, Vocabulary and Manipulation || Sequences || Graphs || Solving Equations and Inequalities

Question Papers

• Deriving Expressions (F) QP
• Expanding Equations (F) QP
• Factorising Equations (F) QP
• Forming Equations (F) QP
• Inputs and Outputs (F) QP
• Manipulation of Formulae (F) QP
• Simplifying Expressions (F) QP
• Substitution into Equations (F) QP

Mark Schemes

• Deriving Expressions (F) MS
• Expanding Equations (F) MS
• Factorising Equations (F) MS
• Forming Equations (F) MS
• Inputs and Outputs (F) MS
• Manipulation of Formulae (F) MS
• Simplifying Expressions (F) MS
• Substitution into Equations (F) MS

Model Answers

• Deriving Expressions (F) MA
• Expanding Equations (F) MA
• Factorising Equations (F) MA
• Forming Equations (F) MA
• Inputs and Outputs (F) MA
• Manipulation of Formulae (F) MA
• Simplifying Expressions (F) MA
• Substitution into Equations (F) MA
• Sequences (F) QP
• Sequences (F) MS
• Sequences (F) MA
• Conversion Graphs (F) QP
• Coordinates (F) QP
• Cubic and Reciprocal Graphs (F) QP
• Distance-time Graphs (F) QP
• Equations of Straight Lines (F) QP
• Graphs of Circles (F) QP
• Graphs of Linear Equations (F) QP
• Graphs of Quadratic Equations (F) QP
• Travel Graphs (F) QP
• Conversion Graphs (F) MS
• Coordinates (F) MS
• Cubic and Reciprocal Graphs (F) MS
• Distance-time Graphs (F) MS
• Equations of Straight Lines (F) MS
• Graphs of Circles (F) MS
• Graphs of Linear Equations (F) MS
• Graphs of Quadratic Equations (F) MS
• Travel Graphs (F) MS
• Conversion Graphs (F) MA
• Coordinates (F) MA
• Cubic and Reciprocal Graphs (F) MA
• Distance-time Graphs (F) MA
• Equations of Straight Lines (F) MA
• Graphs of Circles (F) MA
• Graphs of Linear Equations (F) MA
• Graphs of Quadratic Equations (F) MA
• Travel Graphs (F) MA
• Inequalities (F) QP
• Simultaneous Equations (F) QP
• Solving Linear Equations (F) QP
• Solving using Indices (F) QP
• Inequalities (F) MS
• Simultaneous Equations (F) MS
• Solving Linear Equations (F) MS
• Solving using Indices (F) MS
• Inequalities (F) MA
• Simultaneous Equations (F) MA
• Solving Linear Equations (F) MA
• Solving using Indices (F) MA
• Algebraic Fractions (H) QP
• Algebraic Proof (H) QP
• Deriving Expressions (H) QP
• Expanding Equations (H) QP
• Expanding Triple Brackets (H) QP
• Factorising Equations (H) QP
• Functions (Composite or Inverse) (H) QP
• Manipulation of Formulae (H) QP
• Simplifying Expressions (H) QP
• Solving using Indices (H) QP
• Substitution into Equations (H) QP
• Algebraic Fractions (H) MS
• Algebraic Proof (H) MS
• Deriving Expressions (H) MS
• Expanding Equations (H) MS
• Expanding Triple Brackets (H) MS
• Factorising Equations (H) MS
• Functions (Composite or Inverse) (H) MS
• Manipulation of Formulae (H) MS
• Simplifying Expressions (H) MS
• Solving using Indices (H) MS
• Substitution into Equations (H) MS
• Algebraic Fractions (H) MA
• Algebraic Proof (H) MA
• Deriving Expressions (H) MA
• Expanding Equations (H) MA
• Expanding Triple Brackets (H) MA
• Factorising Equations (H) MA
• Functions (Composite or Inverse) (H) MA
• Manipulation of Formulae (H) MA
• Simplifying Expressions (H) MA
• Solving using Indices (H) MA
• Substitution into Equations (H) MA
• Geometric Progression (H) QP
• Sequences (H) QP
• Geometric Progression (H) MS
• Sequences (H) MS
• Geometric Progression (H) MA
• Sequences (H) MA
• Circles Equations and Tangents (H) QP
• Coordinates (H) QP
• Cubic and Reciprocal Graphs (H) QP
• Distance-time Graphs (H) QP
• Equations of Straight Lines (H) QP
• Exponential and Trigonometric Graphs (H) QP
• Graphs of Circles (H) QP
• Graphs of Linear Equations (H) QP
• Graphs of Quadratic Equations (H) QP
• Interpreting Gradients (H) QP
• Simultaneous Equations on Graphs (H) QP
• Translations and Reflections of Functions (H) QP
• Velocity-time graphs (H) QP
• Circle Equations and Tangents (H) MS
• Coordinates (H) MS
• Cubic and Reciprocal Graphs (H) MS
• Distance-time Graphs (H) MS
• Equations of Straight Lines (H) MS
• Exponential and Trigonometric Graphs (H) MS
• Graphs of Circles (H) MS
• Graphs of Linear Equations (H) MS
• Graphs of Quadratic Equations (H) MS
• Interpreting Gradients (H) MS
• Simultaneous Equations on Graphs (H) MS
• Translations and Reflections of Functions (H) MS
• Velocity-time graphs (H) MS
• Circle Equations and Tangents (H) MA
• Coordinates (H) MA
• Cubic and Reciprocal Graphs (H) MA
• Distance-time Graphs (H) MA
• Equations of Straight Lines (H) MA
• Exponential and Trigonometric Graphs (H) MA
• Graphs of Circles (H) MA
• Graphs of Linear Equations (H) MA
• Graphs of Quadratic Equations (H) MA
• Interpreting Gradients (H) MA
• Simultaneous Equations on Graphs (H) MA
• Translations and Reflections of Functions (H) MA
• Velocity-time graphs (H) MA
• Completing the square (H) QP
• Gradients of Straight Lines (H) QP
• Inequalities (H) QP
• Inequalities on Graphs (H) QP
• Iteration (H) QP
• Quadratic Formula (H) QP
• Quadratic Inequalities (H) QP
• Quadratics Sequences (H) QP
• Simultaneous Equations (H) QP
• Solving Quadratic Equations (H) QP
• Completing the square (H) MS
• Gradients of Straight lines (H) MS
• Inequalities (H) MS
• Inequalities on Graphs (H) MS
• Iteration (H) MS
• Quadratic Formula (H) MS
• Quadratic Inequalities (H) MS
• Quadratic Sequences (H) MS
• Simultaneous Equations (H) MS
• Solving Quadratic Equations (H) MS
• Completing the square (H) MA
• Gradients of Straight lines (H) MA
• Inequalities (H) MA
• Inequalities on Graphs (H) MA
• Iteration (H) MA
• Quadratic Formula (H) MA
• Quadratic Inequalities (H) MA
• Quadratic Sequences (H) MA
• Simultaneous Equations (H) MA
• Solving Quadratic Equations (H) MA

Connect with PMT Education!

• Revision Courses
• Past Papers
• Solution Banks
• University Admissions
• Numerical Reasoning
• Legal Notices

Resourceaholic

Ideas and resources for teaching secondary school mathematics

• Blog Archive

Problem Solving

• Problem Solving Booklet - Complete Mathematics
• GCSE Mathematics - 90 Problem Solving Questions - AQA (and PowerPoint collated by @EJMaths)
• Additional Mathematics Problem Solving Questions (& Teacher Guide ) - AQA
• GCSE Problem Solving  - MEI
• 55 Problems - MathsBox
• Maths problems, puzzles and ideas - Cubed Maths
• UKMT Problems PowerPoint - collated by Dan Walker
• San Gaku Problems - Dan Walker
• Support for Problem Solving  - OCR
• Badger Maths Problem Solving Samples (Years 1 - 6) - via National Stem Centre
• Daily Maths Puzzles (Key Stage 2) - Sarah Farrell
• Mathematical challenges for able pupils in Key Stages 1 and 2 - DfE
• Problem solving with EYFS, Key Stage 1 and Key Stage 2 children - DfE
• Solve My Maths
• Catriona Agg
• Maths Problem Solving
• MathsChallenge.net
• Brilliant.org
• Underground Mathematics
• Openmiddle.com
• United Kingdom Mathematics Trust
• 1001 Math Problems