- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Happiness Hub Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- Happiness Hub
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- College University and Postgraduate
- Academic Writing
Writing Null Hypotheses in Research and Statistics
Last Updated: January 17, 2024 Fact Checked
This article was co-authored by Joseph Quinones and by wikiHow staff writer, Jennifer Mueller, JD . Joseph Quinones is a Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 29,248 times.
Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Start by recognizing that the basic definition of "null" is "none" or "zero"—that's your biggest clue as to what a null hypothesis should say. Keep reading to learn everything you need to know about the null hypothesis, including how it relates to your research question and your alternative hypothesis as well as how to use it in different types of studies.
Things You Should Know
- Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.

- Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.
What is a null hypothesis?

- Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied.
- Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.
Examples of Null Hypotheses

Null Hypothesis vs. Alternative Hypothesis

- For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

- You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step.
- In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.
How do I test a null hypothesis?

- Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. [6] X Research source
- Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. [7] X Research source
- Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. [8] X Research source
- Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables. [9] X Research source
Templates for Null Hypotheses

- Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2].

- Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same.

- Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population.

- Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population.

Expert Q&A

You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about physics, check out our in-depth interview with Joseph Quinones .
- ↑ https://online.stat.psu.edu/stat100/lesson/10/10.1
- ↑ https://online.stat.psu.edu/stat501/lesson/2/2.12
- ↑ https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistics/basic-statistics/supporting-topics/basics/null-and-alternative-hypotheses/
- ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635437/
- ↑ https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing
- ↑ https://education.arcus.chop.edu/null-hypothesis-testing/
- ↑ https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_hypothesistest-means-proportions/bs704_hypothesistest-means-proportions_print.html
About This Article

- Send fan mail to authors
Reader Success Stories
Dec 3, 2022
Did this article help you?

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
wikiHow Tech Help Pro:
Develop the tech skills you need for work and life
Null Hypothesis Examples
ThoughtCo / Hilary Allison
- Scientific Method
- Chemical Laws
- Periodic Table
- Projects & Experiments
- Biochemistry
- Physical Chemistry
- Medical Chemistry
- Chemistry In Everyday Life
- Famous Chemists
- Activities for Kids
- Abbreviations & Acronyms
- Weather & Climate
- Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
- B.A., Physics and Mathematics, Hastings College
In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.
The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.
What Is the Null Hypothesis?
The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.
To distinguish it from other hypotheses , the null hypothesis is written as H 0 (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.
Examples of the Null Hypothesis
To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.
| Are teens better at math than adults? | Age has no effect on mathematical ability. |
| Does taking aspirin every day reduce the chance of having a heart attack? | Taking aspirin daily does not affect heart attack risk. |
| Do teens use cell phones to access the internet more than adults? | Age has no effect on how cell phones are used for internet access. |
| Do cats care about the color of their food? | Cats express no food preference based on color. |
| Does chewing willow bark relieve pain? | There is no difference in pain relief after chewing willow bark versus taking a placebo. |
Other Types of Hypotheses
In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."
Key Takeaways
- In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
- Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
- By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
- What Are Examples of a Hypothesis?
- Random Error vs. Systematic Error
- Six Steps of the Scientific Method
- What Is a Hypothesis? (Science)
- Scientific Method Flow Chart
- What Are the Elements of a Good Hypothesis?
- Scientific Method Vocabulary Terms
- Understanding Simple vs Controlled Experiments
- The Role of a Controlled Variable in an Experiment
- What Is an Experimental Constant?
- What Is a Testable Hypothesis?
- Scientific Hypothesis Examples
- What Is the Difference Between a Control Variable and Control Group?
- DRY MIX Experiment Variables Acronym
- What Is a Controlled Experiment?
- Scientific Variable
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
- Thesis Action Plan New
- Academic Project Planner
Literature Navigator
Thesis dialogue blueprint, writing wizard's template, research proposal compass.
- Why students love us
- Rebels Blog
- Why we are different
- All Products
- Coming Soon
Formulating a Null Hypothesis: Key Elements to Consider

The concept of the null hypothesis is a cornerstone of statistical hypothesis testing. In the article 'Formulating a Null Hypothesis: Key Elements to Consider,' we delve into what a null hypothesis is, why it's crucial for research, and how to properly formulate one. This article offers a comprehensive guide for researchers and students alike, providing the necessary tools to craft a null hypothesis that effectively sets the stage for rigorous scientific inquiry.
Key Takeaways
- A null hypothesis (H0) is a statement that there is no effect or no difference, and it serves as the starting point for statistical testing.
- Formulating a null hypothesis involves defining a clear and concise research question, stating the hypothesis in a way that allows for empirical testing, and considering the potential for Type I errors.
- Evaluating a null hypothesis requires understanding its role in research design, recognizing common misconceptions, and being aware of the challenges in crafting a hypothesis that is both testable and meaningful.
Understanding the Null Hypothesis
Defining the null hypothesis.
The null hypothesis , often represented as H0, is the default assumption that there is no effect or no difference in the context of scientific research. It posits a position of neutrality, suggesting that any observed variations in data are due to chance rather than a specific cause or intervention. Formulating a null hypothesis is a foundational step in hypothesis testing , where it is contrasted with an alternative hypothesis (Ha) that predicts an effect or difference.
Importance of the Null Hypothesis in Research
In the research process, the null hypothesis plays a critical role as it provides a benchmark against which the validity of the study's findings is assessed. It is essential for identifying variables, crafting clear hypotheses, and conducting targeted research that advances scientific knowledge. The research process involves revisiting initial assumptions , evaluating the design, considering alternative explanations, adjusting methodology, and addressing limitations when faced with contradictory data.
Common Misconceptions and Clarifications
There are several misconceptions about the null hypothesis that can lead to confusion. One common error is the belief that a failure to reject the null hypothesis is evidence of no effect, which is not necessarily true. It may simply indicate insufficient evidence to support the alternative hypothesis. Another misunderstanding is equating the null hypothesis with the belief that there is no relationship between variables, which overlooks the fact that it is a tool for statistical testing, not a definitive statement about reality.
Crafting the Null Hypothesis
Steps for formulating a null hypothesis.
When you're learning how to write a thesis or a research paper, formulating a null hypothesis is a critical step. Begin by clearly defining the variables or groups you are studying. Next, state the null hypothesis as a position of no effect or no difference, implying that any observed effect is due to chance. Ensure that your hypothesis is testable and measurable, and consider any potential limitations or biases that could affect the results.
Examples of Null Hypotheses in Various Disciplines
In various academic fields, the null hypothesis takes on different forms. For instance, in psychology, a null hypothesis might state that a new therapy has no effect on depression levels compared to the standard treatment. In ecology, it could assert that there is no significant difference in biodiversity between two protected areas. These examples illustrate how the null hypothesis is tailored to the specific research question and discipline.
Evaluating the Null Hypothesis: Considerations and Challenges
Evaluating the null hypothesis involves selecting appropriate statistical tests and determining the significance level. It's essential to understand the difference between statistical and practical significance . Writing anxiety can arise during this phase, especially when interpreting complex data. However, a systematic approach to hypothesis testing can help alleviate this stress and lead to meaningful research conclusions.
Embarking on the journey of thesis writing can be daunting, but with Research Rebels , you're not alone. Our step-by-step Thesis Action Plan is designed to transform your anxiety and uncertainty into confidence and clarity. From crafting the perfect Null Hypothesis to navigating complex research methodologies, we've got you covered. Don't let sleepless nights hinder your academic success. Visit our website now to claim your special offer and take the first step towards a stress-free thesis experience.
In conclusion, formulating a null hypothesis is a fundamental step in the research process, serving as a critical benchmark against which scientific evidence is measured. A well-constructed null hypothesis provides clarity and direction, allowing for rigorous testing and meaningful interpretation of results. It is essential to articulate the null hypothesis with precision, ensuring it is testable, falsifiable, and appropriately framed to reflect the absence of an effect or relationship. By carefully considering the key elements discussed in this article, researchers can establish a robust foundation for their empirical inquiries, ultimately contributing to the advancement of knowledge within their respective fields.
Frequently Asked Questions
What is the null hypothesis in research.
The null hypothesis (H0) is a statement in research that suggests there is no significant effect or difference between certain populations, conditions, or variables. It is the default assumption that there is no relationship or impact, and it is tested to determine if there is evidence to support an alternative hypothesis.
How do you formulate a null hypothesis?
To formulate a null hypothesis, first identify the research question or problem. Then, state the null hypothesis in a way that it asserts no effect or no difference between groups or variables. It should be clear, specific, and testable, often structured as H0: parameter = value (e.g., H0: μ1 = μ2).
What are common challenges in evaluating the null hypothesis?
Challenges in evaluating the null hypothesis include ensuring the study design and data collection methods are appropriate, selecting the correct statistical test, interpreting the results correctly, and understanding the potential for Type I (false positive) and Type II (false negative) errors.

Discovering Statistics Using IBM SPSS Statistics: A Fun and Informative Guide

Unlocking the Power of Data: A Review of 'Essentials of Modern Business Statistics with Microsoft Excel'

Discovering Statistics Using SAS: A Comprehensive Review

How to Deal with a Total Lack of Motivation, Stress, and Anxiety When Finishing Your Master's Thesis

Mastering the First Step: How to Start Your Thesis with Confidence

Thesis Revision Made Simple: Techniques for Perfecting Your Academic Work

Thesis Action Plan

Integrating Calm into Your Study Routine: The Power of Mindfulness in Education
How to determine the perfect research proposal length.
- Blog Articles
- Affiliate Program
- Terms and Conditions
- Payment and Shipping Terms
- Privacy Policy
- Return Policy
© 2024 Research Rebels, All rights reserved.
Your cart is currently empty.
Null Hypothesis Definition and Examples, How to State
What is the null hypothesis, how to state the null hypothesis, null hypothesis overview.

Why is it Called the “Null”?
The word “null” in this context means that it’s a commonly accepted fact that researchers work to nullify . It doesn’t mean that the statement is null (i.e. amounts to nothing) itself! (Perhaps the term should be called the “nullifiable hypothesis” as that might cause less confusion).
Why Do I need to Test it? Why not just prove an alternate one?
The short answer is, as a scientist, you are required to ; It’s part of the scientific process. Science uses a battery of processes to prove or disprove theories, making sure than any new hypothesis has no flaws. Including both a null and an alternate hypothesis is one safeguard to ensure your research isn’t flawed. Not including the null hypothesis in your research is considered very bad practice by the scientific community. If you set out to prove an alternate hypothesis without considering it, you are likely setting yourself up for failure. At a minimum, your experiment will likely not be taken seriously.

- Null hypothesis : H 0 : The world is flat.
- Alternate hypothesis: The world is round.
Several scientists, including Copernicus , set out to disprove the null hypothesis. This eventually led to the rejection of the null and the acceptance of the alternate. Most people accepted it — the ones that didn’t created the Flat Earth Society !. What would have happened if Copernicus had not disproved the it and merely proved the alternate? No one would have listened to him. In order to change people’s thinking, he first had to prove that their thinking was wrong .
How to State the Null Hypothesis from a Word Problem
You’ll be asked to convert a word problem into a hypothesis statement in statistics that will include a null hypothesis and an alternate hypothesis . Breaking your problem into a few small steps makes these problems much easier to handle.
Step 2: Convert the hypothesis to math . Remember that the average is sometimes written as μ.
H 1 : μ > 8.2
Broken down into (somewhat) English, that’s H 1 (The hypothesis): μ (the average) > (is greater than) 8.2
Step 3: State what will happen if the hypothesis doesn’t come true. If the recovery time isn’t greater than 8.2 weeks, there are only two possibilities, that the recovery time is equal to 8.2 weeks or less than 8.2 weeks.
H 0 : μ ≤ 8.2
Broken down again into English, that’s H 0 (The null hypothesis): μ (the average) ≤ (is less than or equal to) 8.2
How to State the Null Hypothesis: Part Two
But what if the researcher doesn’t have any idea what will happen.
Example Problem: A researcher is studying the effects of radical exercise program on knee surgery patients. There is a good chance the therapy will improve recovery time, but there’s also the possibility it will make it worse. Average recovery times for knee surgery patients is 8.2 weeks.
Step 1: State what will happen if the experiment doesn’t make any difference. That’s the null hypothesis–that nothing will happen. In this experiment, if nothing happens, then the recovery time will stay at 8.2 weeks.
H 0 : μ = 8.2
Broken down into English, that’s H 0 (The null hypothesis): μ (the average) = (is equal to) 8.2
Step 2: Figure out the alternate hypothesis . The alternate hypothesis is the opposite of the null hypothesis. In other words, what happens if our experiment makes a difference?
H 1 : μ ≠ 8.2
In English again, that’s H 1 (The alternate hypothesis): μ (the average) ≠ (is not equal to) 8.2
That’s How to State the Null Hypothesis!
Check out our Youtube channel for more stats tips!
Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial. Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences , Wiley.
Module 9: Hypothesis Testing With One Sample
Null and alternative hypotheses, learning outcomes.
- Describe hypothesis testing in general and in practice
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make adecision. There are two options for a decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40
- H 0 : p = 0.40
- H a : p > 0.40
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.
Formula Review
H 0 and H a are contradictory.
- OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
- Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
10.1 - setting the hypotheses: examples.
A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.
Example 10.2: Hypotheses with One Sample of One Categorical Variable Section
About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.
- Research Question : Are artists more likely to be left-handed than people found in the general population?
- Response Variable : Classification of the student as either right-handed or left-handed
State Null and Alternative Hypotheses
- Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
- Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.
Example 10.3: Hypotheses with One Sample of One Measurement Variable Section

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.
- Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
- Response Variable : dosage of the active ingredient found by a chemical assay.
- Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
- Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.
Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.
- Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
- Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
- Explanatory (Grouping) Variable: Sex
- Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
- Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.
Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.
- Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
- Response Variable : Weight loss (pounds)
- Explanatory (Grouping) Variable : Type of diet
- Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
- Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.
Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section
- Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
- Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
- Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
- Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.
This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.
Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section
- Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
- Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
- Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
- Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.
Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section
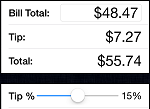
- Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
- Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
- Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
- Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, automatically generate references for free.
- Knowledge Base
- Methodology
- How to Write a Strong Hypothesis | Guide & Examples
How to Write a Strong Hypothesis | Guide & Examples
Published on 6 May 2022 by Shona McCombes .
A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection.
Table of contents
What is a hypothesis, developing a hypothesis (with example), hypothesis examples, frequently asked questions about writing hypotheses.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).
Variables in hypotheses
Hypotheses propose a relationship between two or more variables . An independent variable is something the researcher changes or controls. A dependent variable is something the researcher observes and measures.
In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .
Prevent plagiarism, run a free check.
Step 1: ask a question.
Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.
Step 2: Do some preliminary research
Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.
At this stage, you might construct a conceptual framework to identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalise more complex constructs.
Step 3: Formulate your hypothesis
Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.
Step 4: Refine your hypothesis
You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:
- The relevant variables
- The specific group being studied
- The predicted outcome of the experiment or analysis
Step 5: Phrase your hypothesis in three ways
To identify the variables, you can write a simple prediction in if … then form. The first part of the sentence states the independent variable and the second part states the dependent variable.
In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.
If you are comparing two groups, the hypothesis can state what difference you expect to find between them.
Step 6. Write a null hypothesis
If your research involves statistical hypothesis testing , you will also have to write a null hypothesis. The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .
| Research question | Hypothesis | Null hypothesis |
|---|---|---|
| What are the health benefits of eating an apple a day? | Increasing apple consumption in over-60s will result in decreasing frequency of doctor’s visits. | Increasing apple consumption in over-60s will have no effect on frequency of doctor’s visits. |
| Which airlines have the most delays? | Low-cost airlines are more likely to have delays than premium airlines. | Low-cost and premium airlines are equally likely to have delays. |
| Can flexible work arrangements improve job satisfaction? | Employees who have flexible working hours will report greater job satisfaction than employees who work fixed hours. | There is no relationship between working hour flexibility and job satisfaction. |
| How effective is secondary school sex education at reducing teen pregnancies? | Teenagers who received sex education lessons throughout secondary school will have lower rates of unplanned pregnancy than teenagers who did not receive any sex education. | Secondary school sex education has no effect on teen pregnancy rates. |
| What effect does daily use of social media have on the attention span of under-16s? | There is a negative correlation between time spent on social media and attention span in under-16s. | There is no relationship between social media use and attention span in under-16s. |
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis is not just a guess. It should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
McCombes, S. (2022, May 06). How to Write a Strong Hypothesis | Guide & Examples. Scribbr. Retrieved 29 August 2024, from https://www.scribbr.co.uk/research-methods/hypothesis-writing/
Is this article helpful?
Shona McCombes
Other students also liked, operationalisation | a guide with examples, pros & cons, what is a conceptual framework | tips & examples, a quick guide to experimental design | 5 steps & examples.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Methodology
- How to Write a Strong Hypothesis | Steps & Examples
How to Write a Strong Hypothesis | Steps & Examples
Published on May 6, 2022 by Shona McCombes . Revised on November 20, 2023.
A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection .
Example: Hypothesis
Daily apple consumption leads to fewer doctor’s visits.
Table of contents
What is a hypothesis, developing a hypothesis (with example), hypothesis examples, other interesting articles, frequently asked questions about writing hypotheses.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Variables in hypotheses
Hypotheses propose a relationship between two or more types of variables .
- An independent variable is something the researcher changes or controls.
- A dependent variable is something the researcher observes and measures.
If there are any control variables , extraneous variables , or confounding variables , be sure to jot those down as you go to minimize the chances that research bias will affect your results.
In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .
Prevent plagiarism. Run a free check.
Step 1. ask a question.
Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.
Step 2. Do some preliminary research
Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.
At this stage, you might construct a conceptual framework to ensure that you’re embarking on a relevant topic . This can also help you identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalize more complex constructs.
Step 3. Formulate your hypothesis
Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.
4. Refine your hypothesis
You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:
- The relevant variables
- The specific group being studied
- The predicted outcome of the experiment or analysis
5. Phrase your hypothesis in three ways
To identify the variables, you can write a simple prediction in if…then form. The first part of the sentence states the independent variable and the second part states the dependent variable.
In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.
If you are comparing two groups, the hypothesis can state what difference you expect to find between them.
6. Write a null hypothesis
If your research involves statistical hypothesis testing , you will also have to write a null hypothesis . The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .
- H 0 : The number of lectures attended by first-year students has no effect on their final exam scores.
- H 1 : The number of lectures attended by first-year students has a positive effect on their final exam scores.
| Research question | Hypothesis | Null hypothesis |
|---|---|---|
| What are the health benefits of eating an apple a day? | Increasing apple consumption in over-60s will result in decreasing frequency of doctor’s visits. | Increasing apple consumption in over-60s will have no effect on frequency of doctor’s visits. |
| Which airlines have the most delays? | Low-cost airlines are more likely to have delays than premium airlines. | Low-cost and premium airlines are equally likely to have delays. |
| Can flexible work arrangements improve job satisfaction? | Employees who have flexible working hours will report greater job satisfaction than employees who work fixed hours. | There is no relationship between working hour flexibility and job satisfaction. |
| How effective is high school sex education at reducing teen pregnancies? | Teenagers who received sex education lessons throughout high school will have lower rates of unplanned pregnancy teenagers who did not receive any sex education. | High school sex education has no effect on teen pregnancy rates. |
| What effect does daily use of social media have on the attention span of under-16s? | There is a negative between time spent on social media and attention span in under-16s. | There is no relationship between social media use and attention span in under-16s. |
If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.
- Sampling methods
- Simple random sampling
- Stratified sampling
- Cluster sampling
- Likert scales
- Reproducibility
Statistics
- Null hypothesis
- Statistical power
- Probability distribution
- Effect size
- Poisson distribution
Research bias
- Optimism bias
- Cognitive bias
- Implicit bias
- Hawthorne effect
- Anchoring bias
- Explicit bias
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
McCombes, S. (2023, November 20). How to Write a Strong Hypothesis | Steps & Examples. Scribbr. Retrieved August 30, 2024, from https://www.scribbr.com/methodology/hypothesis/
Is this article helpful?
Shona McCombes
Other students also liked, construct validity | definition, types, & examples, what is a conceptual framework | tips & examples, operationalization | a guide with examples, pros & cons, what is your plagiarism score.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 13: Inferential Statistics
Understanding Null Hypothesis Testing
Learning Objectives
- Explain the purpose of null hypothesis testing, including the role of sampling error.
- Describe the basic logic of null hypothesis testing.
- Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
The Purpose of Null Hypothesis Testing
As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)
One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any statistical relationship in a sample can be interpreted in two ways:
- There is a relationship in the population, and the relationship in the sample reflects this.
- There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.
The Logic of Null Hypothesis Testing
Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
- Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
- Determine how likely the sample relationship would be if the null hypothesis were true.
- If the sample relationship would be extremely unlikely, then reject the null hypothesis in favour of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”
The Misunderstood p Value
The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.
Role of Sample Size and Relationship Strength
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”
| Sample Size | Weak relationship | Medium-strength relationship | Strong relationship |
|---|---|---|---|
| Small ( = 20) | No | No | = Maybe = Yes |
| Medium ( = 50) | No | Yes | Yes |
| Large ( = 100) | = Yes = No | Yes | Yes |
| Extra large ( = 500) | Yes | Yes | Yes |
Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.
Statistical Significance Versus Practical Significance
Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.
Key Takeaways
- Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
- The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
- The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
- Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
- Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
- The correlation between two variables is r = −.78 based on a sample size of 137.
- The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
- In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
- In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
- A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Long Descriptions
“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]
“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]
Media Attributions
- Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
- Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
- Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
- Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵
Values in a population that correspond to variables measured in a study.
The random variability in a statistic from sample to sample.
A formal approach to deciding between two interpretations of a statistical relationship in a sample.
The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.
The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.
When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.
The probability that, if the null hypothesis were true, the result found in the sample would occur.
How low the p value must be before the sample result is considered unlikely in null hypothesis testing.
When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.
Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
- Math Article
Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .
In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.
Table of contents:
- Comparison with Alternative Hypothesis
Null Hypothesis Definition
The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .
Null Hypothesis Symbol
In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .
Null Hypothesis Principle
The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.
Null Hypothesis Formula
Here, the hypothesis test formulas are given below for reference.
The formula for the null hypothesis is:
H 0 : p = p 0
The formula for the alternative hypothesis is:
H a = p >p 0 , < p 0 ≠ p 0
The formula for the test static is:
Remember that, p 0 is the null hypothesis and p – hat is the sample proportion.
Also, read:
Types of Null Hypothesis
There are different types of hypothesis. They are:
Simple Hypothesis
It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.
Composite Hypothesis
The composite hypothesis is one that does not completely specify the population distribution.
Exact Hypothesis
Exact hypothesis defines the exact value of the parameter. For example μ= 50
Inexact Hypothesis
This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60
Null Hypothesis Rejection
Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.
How do you Find the Null Hypothesis?
The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).
When is Null Hypothesis Rejected?
The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.
Null Hypothesis and Alternative Hypothesis
Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.
|
|
| |
| 1 | The null hypothesis is a statement. There exists no relation between two variables | Alternative hypothesis a statement, there exists some relationship between two measured phenomenon |
| 2 | Denoted by H | Denoted by H |
| 3 | The observations of this hypothesis are the result of chance | The observations of this hypothesis are the result of real effect |
| 4 | The mathematical formulation of the null hypothesis is an equal sign | The mathematical formulation alternative hypothesis is an inequality sign such as greater than, less than, etc. |
Null Hypothesis Examples
Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.
If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.
Few more examples are:
1). Are there is 100% chance of getting affected by dengue?
Ans: There could be chances of getting affected by dengue but not 100%.
2). Do teenagers are using mobile phones more than grown-ups to access the internet?
Ans: Age has no limit on using mobile phones to access the internet.
3). Does having apple daily will not cause fever?
Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.
4). Do the children more good in doing mathematical calculations than grown-ups?
Ans: Age has no effect on Mathematical skills.
In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives.
The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data.
Frequently Asked Questions on Null Hypothesis
What is meant by the null hypothesis.
In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.
What are the benefits of hypothesis testing?
Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.
When a null hypothesis is accepted and rejected?
The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.
Why is the null hypothesis important?
The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.
How to accept or reject the null hypothesis in the chi-square test?
If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Hypothesis Testing (cont...)
Hypothesis testing, the null and alternative hypothesis.
In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.
The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:
| Null Hypotheses (H ): | Undertaking seminar classes has no effect on students' performance. |
| Alternative Hypothesis (H ): | Undertaking seminar class has a positive effect on students' performance. |
Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:
| Null Hypotheses (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is the same in the population. |
| Alternative Hypothesis (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is not the same in the population. |
Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.
Significance levels
The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?
So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.
Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions
When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:
| Alternative Hypothesis (H ): | Undertaking seminar classes has a positive effect on students' performance. |
The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.
Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.
Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:
| Alternative Hypothesis (H ): | Undertaking seminar classes has an effect on students' performance. |
In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.
Rejecting or failing to reject the null hypothesis
Let's return finally to the question of whether we reject or fail to reject the null hypothesis.
If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.
Null hypothesis and Alternative Hypothesis
A hypothesis is a proposed explanation for a phenomenon, based on observation, reasoning, or scientific theory, awaiting verification or falsification through experimentation and data analysis. It serves as a starting point for investigation, guiding the research process by suggesting what outcomes to expect. In the realm of statistics and scientific research, hypotheses are crucial for designing experiments, analyzing results, and advancing knowledge.
The null hypothesis and alternative hypothesis are required to be fragmented properly before the data collection and interpretation phase in the research. Well fragmented hypotheses indicate that the researcher has adequate knowledge in that particular area and is thus able to take the investigation further because they can use a much more systematic system. It gives direction to the researcher on his/her collection and interpretation of data.
The null hypothesis and alternative hypothesis are useful only if they state the expected relationship between the variables or if they are consistent with the existing body of knowledge. They should be expressed as simply and concisely as possible. They are useful if they have explanatory power.
The purpose and importance of the null hypothesis and alternative hypothesis are that they provide an approximate description of the phenomena. The purpose is to provide the researcher or an investigator with a relational statement that is directly tested in a research study. The purpose is to provide the framework for reporting the inferences of the study. The purpose is to behave as a working instrument of the theory. The purpose is to prove whether or not the test is supported, which is separated from the investigator’s own values and decisions. They also provide direction to the research.
Need help with your analysis?
Schedule a time to speak with an expert using the calendar below.
The null hypothesis is generally denoted as H0. It states the exact opposite of what an investigator or an experimenter predicts or expects. It basically defines the statement which states that there is no exact or actual relationship between the variables.
The alternative hypothesis is generally denoted as H1. It makes a statement that suggests or advises a potential result or an outcome that an investigator or the researcher may expect. It has been categorized into two categories: directional alternative hypothesis and non directional alternative hypothesis.
The directional hypothesis is a kind that explains the direction of the expected findings. Sometimes this type of alternative hypothesis is developed to examine the relationship among the variables rather than a comparison between the groups.
The non directional hypothesis is a kind that has no definite direction of the expected findings being specified.
Related Pages:
Hypothesis Testing
Research Hypotheses
Ready to test your hypothesis? Check out Intellectus Statistics , the easy to use statistics software for the non-statistician.

Transcription Service for Your Academic Paper
Start Transcription now
Editing & Proofreading for Your Research Paper
Get it proofread now
Online Printing & Binding with Free Express Delivery
Configure binding now
- Academic essay overview
- The writing process
- Structuring academic essays
- Types of academic essays
- Academic writing overview
- Sentence structure
- Academic writing process
- Improving your academic writing
- Titles and headings
- APA style overview
- APA citation & referencing
- APA structure & sections
- Citation & referencing
- Structure and sections
- APA examples overview
- Commonly used citations
- Other examples
- British English vs. American English
- Chicago style overview
- Chicago citation & referencing
- Chicago structure & sections
- Chicago style examples
- Citing sources overview
- Citation format
- Citation examples
- College essay overview
- Application
- How to write a college essay
- Types of college essays
- Commonly confused words
- Definitions
- Dissertation overview
- Dissertation structure & sections
- Dissertation writing process
- Graduate school overview
- Application & admission
- Study abroad
- Master degree
- Harvard referencing overview
- Language rules overview
- Grammatical rules & structures
- Parts of speech
- Punctuation
- Methodology overview
- Analyzing data
- Experiments
- Observations
- Inductive vs. Deductive
- Qualitative vs. Quantitative
- Types of validity
- Types of reliability
- Sampling methods
- Theories & Concepts
- Types of research studies
- Types of variables
- MLA style overview
- MLA examples
- MLA citation & referencing
- MLA structure & sections
- Plagiarism overview
- Plagiarism checker
- Types of plagiarism
- Printing production overview
- Research bias overview
- Types of research bias
- Example sections
- Types of research papers
- Research process overview
- Problem statement
- Research proposal
- Research topic
- Statistics overview
- Levels of measurment
- Frequency distribution
- Measures of central tendency
- Measures of variability
- Hypothesis testing
- Parameters & test statistics
- Types of distributions
- Correlation
- Effect size
- Hypothesis testing assumptions
- Types of ANOVAs
- Types of chi-square
- Statistical data
- Statistical models
- Spelling mistakes
- Tips overview
- Academic writing tips
- Dissertation tips
- Sources tips
- Working with sources overview
- Evaluating sources
- Finding sources
- Including sources
- Types of sources
Your Step to Success
Transcription Service for Your Paper
Printing & Binding with 3D Live Preview
Null Hypothesis And Alternative Hypothesis
How do you like this article cancel reply.
Save my name, email, and website in this browser for the next time I comment.
The null hypothesis and alternative hypothesis are cornerstones in statistics and hypothesis testing. They represent a methodology used to validate or refute claims about a population based on sample data. The process involves assuming the null hypothesis is true and using statistical analysis to test if the observed data fit this assumption. This article delves into the key roles, calculations, and formulation of the null and alternative hypotheses.
Inhaltsverzeichnis
- 1 Null and Alternative Hypothesis – In a Nutshell
- 2 Definition: Null and alternative hypotheses
- 3 Null/Alternative hypotheses: Research questions
- 4 The null hypothesis (H0)
- 5 The alternative hypothesis (Ha)
- 6 Null hypothesis vs. alternative hypothesis
- 7 Writing null and alternative hypotheses correctly
Null and Alternative Hypothesis – In a Nutshell
This article describes the academic conventions you need to follow when writing about these hypotheses, including:
- The specific wording to be used.
- Which tests can be used to test the hypotheses.
- Similarities and differences between both hypotheses.
- Statistical expressions you can use to write your conclusions regarding each hypothesis.
Definition: Null and alternative hypotheses
These two hypotheses are used in statistical testing to prove or disprove a theory.
- The null hypothesis always states that there’s no statistically significant relationship between variables.
- The alternative hypothesis states the opposite.
The null hypothesis (H 0 ) assumes there is no significant difference between specified populations or no association among groups. This is often considered the default or status quo hypothesis, indicating no change or effect.
The alternative hypothesis (H a or H 1 ) is the counterpart to the null hypothesis and claims that there is a significant difference or association among groups. It represents a statement of what a statistical hypothesis test is set up to establish.
You want to test whether a drug has an effect on a disease.
- Null hypothesis: There is no effect of the drug on the disease
- Alternative hypothesis: There is an effect (either positive or negative) of the drug on the disease.
Null/Alternative hypotheses: Research questions
These hypotheses function as tentative answers to research questions . Therefore, you can’t have an answer to your research questions without confirming or rejecting either hypothesis.
Both hypotheses are tested using statistical tests that compare two population samples/groups. Testing confirms or rejects the hypotheses, by showing whether there’s a relationship between an independent variable and a dependent variable.
The null hypothesis (H 0 )
The null hypothesis states that there’s no statistically significant relationship or effect between variables.
Based on test results, the null hypothesis can be rejected, which means there is a significant relationship between the variables – one affects the other.
Null hypothesis (H 0 ): The number of hours of sleep has no effect on short-term memory.
- If statistical testing shows that hours of sleep do affect memory, H 0 is rejected .
- If testing shows that memory stays the same irrespective of hours of sleep, you fail to reject H 0 .
When writing about null hypotheses, you can only reject them or fail to reject them. Don’t use expressions like accepting, proving, or disproving.
Depending on sample size and testing method, you can incur errors when determining the validity of null hypotheses.
- A Type I error happens if you reject H 0 and claim there’s a significant relationship between the variables, even though test results don’t support this claim.
- A Type II error happens if you fail to reject H 0 and claim there’s no relationship between variables, even though testing proves otherwise.
Examples of null hypotheses
The table below illustrates null hypotheses for their respective research question:
| Exercise has no effect on heart disease risk | |
| Age has no effect on employability |
Common statistical tests used to reject H 0 include:
- Pearson correlation
- Linear regression
In the paper’s Methods section, you must indicate which test you used.
The alternative hypothesis (H a )
The alternative hypothesis ( H a or H 1 ) claims there’s a statistically significant relationship between variables.
Because H a is the opposite of what the null hypothesis claims, accepting H a means rejecting H 0 and vice versa.
When reporting alternative hypotheses, you can only say that H a is supported or not supported by test data. Don’t use expressions like accept, reject, disprove, confirm, etc.
Examples of alternative hypotheses
The table below shows alternative hypotheses for their respective research question:
| Exercise has an effect on heart disease risk | |
| Age has an effect on employability |
Common statistical tests used to support the alternative hypothesis include:
Null hypothesis vs. alternative hypothesis
Both hypotheses provide possible but mutually exclusive answers to a research question. They can only be rejected or supported through statistical testing.
The differences between them are:
| ) | ) |
| Claims there’s relationship between variables. | Claims there a relationship between variables. |
| Common expressions used to write it include no relationship, no effect, no difference, no increase, no decrease, and no change. | Common expressions used to write it include a relationship, an effect, a difference, an increase, a decrease, and a change. |
| If testing shows there’s a relationship, this is reported as p ≤ α, therefore H is . | If testing shows there’s a relationship, this is reported as p ≤ α, therefore H is . |
| If testing shows there’s no relationship, this is reported as p > α, therefore we H . | If testing shows no relationship, this is reported as p > α, therefore H is . |
Writing null and alternative hypotheses correctly
To write these hypotheses correctly in your essay, make sure you:
- Write your research question, mentioning both independent and dependent variables
- State the null hypothesis
- State the alternative hypothesis.
Does exercise improve depressive symptoms?
Exercise = independent variable
Depressive symptoms = dependent variable
- H 0 = Exercise doesn’t improve depressive symptoms.
- H a = Exercise improves depressive symptoms.
For specific tests, use the following wording:
| The mean dependent variable has no effect on sample 1 (µ1) and sample 2 (µ2); µ1 = µ2 | The mean dependent variable has an effect on sample 1 (µ1) and sample 2 (µ2); µ1 ≠ µ2. | |
| The mean dependent variable has no effect on sample/group 1 (µ1) and sample/group 2 (µ2); µ1 = µ2 | The mean dependent variable (µ1) and sample/group 2 (µ2) are not all equal; µ1 ≠ µ2 ≠ µ3. | |
| There’s no correlation between the independent variable and the dependent variable: ρ = 0. | There's a correlation between the independent variable and ρ = 0 the dependent variable; ρ ≠ 0. | |
| There’s no relationship between the independent variable and the dependent variable; β1 = 0. | There’s a relationship between the independent variable and the dependent variable; β1 ≠ 0. | |
| The dependent variable expressed as a proportion doesn’t differentiate between sample/group 1 (ρ1) and sample/group 2 (ρ2); ρ1 = ρ2. | The dependent variable expressed as proportion differentiates between sample/group 1 (ρ1) and sample/group 2 (ρ2); p1 ≠ p2. |
Printing Your Thesis With BachelorPrint
- High-quality bindings with customizable embossing
- 3D live preview to check your work before ordering
- Free express delivery
Configure your binding now!
to the print shop
What are null and alternative hypotheses?
They’re unproven statements about a research question.
The null hypothesis says there’s a relationship between variables, and the alternative hypothesis claims there isn’t one.
Can I only test one hypothesis?
No, these hypotheses are competing statements, so when you test one hypothesis, you automatically test the other.
How do I write H0 and Ha using mathematical symbols?
The mathematical symbol used to write H 0 is = For H a , the symbol is ≠
Which type of tests can I use to test H0 and Ha?
In most cases, one-tailed tests are best.
They did such an excellent job printing my dissertation! I got it fast and...
We use cookies on our website. Some of them are essential, while others help us to improve this website and your experience.
- External Media
Individual Privacy Preferences
Cookie Details Privacy Policy Imprint
Here you will find an overview of all cookies used. You can give your consent to whole categories or display further information and select certain cookies.
Accept all Save
Essential cookies enable basic functions and are necessary for the proper function of the website.
Show Cookie Information Hide Cookie Information
| Name | |
|---|---|
| Anbieter | Eigentümer dieser Website, |
| Zweck | Speichert die Einstellungen der Besucher, die in der Cookie Box von Borlabs Cookie ausgewählt wurden. |
| Cookie Name | borlabs-cookie |
| Cookie Laufzeit | 1 Jahr |
| Name | |
|---|---|
| Anbieter | Bachelorprint |
| Zweck | Erkennt das Herkunftsland und leitet zur entsprechenden Sprachversion um. |
| Datenschutzerklärung | |
| Host(s) | ip-api.com |
| Cookie Name | georedirect |
| Cookie Laufzeit | 1 Jahr |
| Name | |
|---|---|
| Anbieter | Playcanvas |
| Zweck | Display our 3D product animations |
| Datenschutzerklärung | |
| Host(s) | playcanv.as, playcanvas.as, playcanvas.com |
| Cookie Laufzeit | 1 Jahr |
Statistics cookies collect information anonymously. This information helps us to understand how our visitors use our website.
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Google Ireland Limited, Gordon House, Barrow Street, Dublin 4, Ireland |
| Zweck | Cookie von Google zur Steuerung der erweiterten Script- und Ereignisbehandlung. |
| Datenschutzerklärung | |
| Cookie Name | _ga,_gat,_gid |
| Cookie Laufzeit | 2 Jahre |
Content from video platforms and social media platforms is blocked by default. If External Media cookies are accepted, access to those contents no longer requires manual consent.
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Meta Platforms Ireland Limited, 4 Grand Canal Square, Dublin 2, Ireland |
| Zweck | Wird verwendet, um Facebook-Inhalte zu entsperren. |
| Datenschutzerklärung | |
| Host(s) | .facebook.com |
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Google Ireland Limited, Gordon House, Barrow Street, Dublin 4, Ireland |
| Zweck | Wird zum Entsperren von Google Maps-Inhalten verwendet. |
| Datenschutzerklärung | |
| Host(s) | .google.com |
| Cookie Name | NID |
| Cookie Laufzeit | 6 Monate |
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Meta Platforms Ireland Limited, 4 Grand Canal Square, Dublin 2, Ireland |
| Zweck | Wird verwendet, um Instagram-Inhalte zu entsperren. |
| Datenschutzerklärung | |
| Host(s) | .instagram.com |
| Cookie Name | pigeon_state |
| Cookie Laufzeit | Sitzung |
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Openstreetmap Foundation, St John’s Innovation Centre, Cowley Road, Cambridge CB4 0WS, United Kingdom |
| Zweck | Wird verwendet, um OpenStreetMap-Inhalte zu entsperren. |
| Datenschutzerklärung | |
| Host(s) | .openstreetmap.org |
| Cookie Name | _osm_location, _osm_session, _osm_totp_token, _osm_welcome, _pk_id., _pk_ref., _pk_ses., qos_token |
| Cookie Laufzeit | 1-10 Jahre |
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Twitter International Company, One Cumberland Place, Fenian Street, Dublin 2, D02 AX07, Ireland |
| Zweck | Wird verwendet, um Twitter-Inhalte zu entsperren. |
| Datenschutzerklärung | |
| Host(s) | .twimg.com, .twitter.com |
| Cookie Name | __widgetsettings, local_storage_support_test |
| Cookie Laufzeit | Unbegrenzt |
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Vimeo Inc., 555 West 18th Street, New York, New York 10011, USA |
| Zweck | Wird verwendet, um Vimeo-Inhalte zu entsperren. |
| Datenschutzerklärung | |
| Host(s) | player.vimeo.com |
| Cookie Name | vuid |
| Cookie Laufzeit | 2 Jahre |
| Akzeptieren | |
|---|---|
| Name | |
| Anbieter | Google Ireland Limited, Gordon House, Barrow Street, Dublin 4, Ireland |
| Zweck | Wird verwendet, um YouTube-Inhalte zu entsperren. |
| Datenschutzerklärung | |
| Host(s) | google.com |
| Cookie Name | NID |
| Cookie Laufzeit | 6 Monate |
Privacy Policy Imprint
- Privacy Policy

Home » What is a Hypothesis – Types, Examples and Writing Guide
What is a Hypothesis – Types, Examples and Writing Guide
Table of Contents

Definition:
Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.
Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.
Types of Hypothesis
Types of Hypothesis are as follows:
Research Hypothesis
A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.
Null Hypothesis
The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.
Alternative Hypothesis
An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.
Directional Hypothesis
A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.
Non-directional Hypothesis
A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.
Statistical Hypothesis
A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.
Composite Hypothesis
A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.
Empirical Hypothesis
An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.
Simple Hypothesis
A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.
Complex Hypothesis
A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.
Applications of Hypothesis
Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:
- Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
- Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
- Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
- Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
- Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
- Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.
How to write a Hypothesis
Here are the steps to follow when writing a hypothesis:
Identify the Research Question
The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.
Conduct a Literature Review
Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.
Determine the Variables
The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.
Formulate the Hypothesis
Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.
Write the Null Hypothesis
The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.
Refine the Hypothesis
After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.
Examples of Hypothesis
Here are a few examples of hypotheses in different fields:
- Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
- Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
- Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
- Education : “Implementing a new teaching method will result in higher student achievement scores.”
- Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
- Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
- Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”
Purpose of Hypothesis
The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.
The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.
In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.
When to use Hypothesis
Here are some common situations in which hypotheses are used:
- In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
- In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
- I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.
Characteristics of Hypothesis
Here are some common characteristics of a hypothesis:
- Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
- Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
- Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
- Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
- Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
- Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
- Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.
Advantages of Hypothesis
Hypotheses have several advantages in scientific research and experimentation:
- Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
- Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
- Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
- Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
- Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
- Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.
Limitations of Hypothesis
Some Limitations of the Hypothesis are as follows:
- Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
- May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
- May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
- Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
- Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
- May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.
About the author
Muhammad Hassan
Researcher, Academic Writer, Web developer
You may also like

Background of The Study – Examples and Writing...

Research Problem – Examples, Types and Guide

Figures in Research Paper – Examples and Guide

Evaluating Research – Process, Examples and...

Scope of the Research – Writing Guide and...

Dissertation – Format, Example and Template
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Is it possible not to have a hypothesis in your thesis? [closed]
I have been working on a research report in which forecasting is done on the basis of data, followed by an interpretation of the forecasted results.
Is it possible to have that kind of research without hypothesizing any statement?
If this question is off-topic kindly recommend a suitable community.
- research-process
- methodology
- Would you please provide context for your thesis. For example, what is your area of study and what subfield are you in? – Richard Erickson Commented Jun 14, 2017 at 17:50
- It would be answerable, if you could please add some more details as suggsted by @RichardErickson. – Coder Commented Jun 14, 2017 at 18:02
- 3 This question is not about academia but about statistics. It might be on-topic on crossvalidated.se – henning no longer feeds AI Commented Jun 15, 2017 at 5:58
- 2 @henning I made it about statistics, but the question as it stands is about research protocol. On crossvalidated Ibn e Ashiq can ask how to do the statistics. – Joris Meys Commented Jun 15, 2017 at 8:52
As a statistician, I'm inclined to say "no, you can't" as a short answer. Reason for this is simple: even in complete random datasets on average 5% of the correlations will be significant when tested in a model. So if you rely on only the data to make any kind of interpretation on association of variables, you're bound to publish false positives. This has been discussed for decades, eg this rather strong opinion of Ioannidis (2005) :
http://journals.plos.org/plosmedicine/article?id=10.1371/journal.pmed.0020124
Bias can entail manipulation in the analysis or reporting of findings. Selective or distorted reporting is a typical form of such bias.
If you don't formulate a hypothesis and still interprete the data, you're -probably unintentionally- reporting selectively. You select from the analysis those results that tell a story, and in doing so, you're likely to report something that isn't a solid association or relation.
That said, you don't always have to formulate a specific hypothesis. For example, if you compare multiple methods on efficiency, you don't have to hypothesize beforehand which one is going to be the best. But the statistical test you use for comparison, will imply a "null hypothesis" that there is no real difference between all methods. Also this is "formulating a hypothesis" merely by the choice of analysis tools.
And this is even more important to realize: you might not formulate a hypothesis explicitly, but the nature of the statistical tools you use to come to your interpretation, will imply a set of rather rigid hypotheses and assumptions. You need to be aware of those hypotheses and also of those assumptions.
Because that's something I see far too often: people not explicitly formulating a hypothesis, still interpreting results from a statistical methodology, but failing to realize that their data does not meet the assumptions of that methodology. And that invalidates your entire interpretation.
This problem is even more stringent when forecasting. If you use regression models, you should be aware that predictions outside the boundaries of the original data cannot be interpreted. The uncertainty on those predictions is simply too big. If you use spline methods, you can even get into trouble at the edge of your original data. So definitely in the case of forecasting I would write out both the goal of the research and what you expect the predictions to show, including the scientific reason why. Only in those cases you can use forecasts as some form of evidence for or against the expected relation. If you don't do that, your forecasting model might as well be a fancy random number generator.
So in conclusion: even if your research goal isn't necessarily a defined hypothesis, you still need to formulate the hypotheses you want to test before carrying out the actual statistical tests.
And in all honesty, writing down what you expect to see is always a good idea, even if it's only to order your own thoughts.
- 1 +1 This is a really important point and a core principle of the scientific method, but for some reason many people either ignore it (out of convenience) or do not know about it. – 101010111100 Commented Jun 14, 2017 at 18:38
- There are fields - especially in Engineering - where results do not depend on a statistical analysis so as non-statistician, I would say, yes you can write a thesis without a hypothesis. – o4tlulz Commented Jun 15, 2017 at 4:04
- 1 @Kevin That's using cross-validation, an often used statistical technique with its own assumptions. If you do that, you have to keep in mind that your training data and testing data have to be completely independent, or any hypothesis testing (yes, also there you test a hypothesis) is invalid. Independence is one of the most important assumptions in about every common statistical technique. – Joris Meys Commented Jun 15, 2017 at 8:47
- 1 @Ooker I always tell my students to only use methods they know and understand. You can't know everything about statistics. But what you need to know, is all the details of the techniques you use yourself. And in any case every student should have the knowledge of the basic tests used in the majority of papers. Because if you don't understand those, there's no way you can evaluate yourself whether the conclusion in a paper actually makes sense. – Joris Meys Commented Jun 15, 2017 at 8:51
- 1 @o4tlulz and how do you assure me that it solves the issue? Can you prove that? Can you show me your "solution" isn't just random luck? – Joris Meys Commented Jun 16, 2017 at 7:45
Not the answer you're looking for? Browse other questions tagged phd research-process thesis methodology .
- Featured on Meta
- Bringing clarity to status tag usage on meta sites
- Announcing a change to the data-dump process
Hot Network Questions
- What prevents a browser from saving and tracking passwords entered to a site?
- How to remove obligation to run as administrator in Windows?
- Which version of Netscape, on which OS, appears in the movie “Cut” (2000)?
- Do the amplitude and frequency of gravitational waves emitted by binary stars change as the stars get closer together?
- Whatever happened to Chessmaster?
- Math format bug for \mathbf command in TeXLive 2023/2024
- How much easier/harder would it be to colonize space if humans found a method of giving ourselves bodies that could survive in almost anything?
- Took a pic of old school friend in the 80s who is now quite famous and written a huge selling memoir. Pic has ben used in book without permission
- Parse Minecraft's VarInt
- 1960s Stylesheet/Format for working Physics problems
- Which hash algorithms support binary input of arbitrary bit length?
- Maximizing the common value of both sides of an equation
- Writing an i with a line over it instead of an i with a dot and a line over it
- Can unlimited Duration spells be Dismissed?
- If the Hom-space of finite length modules is generated by single elements, must the elements be conjugate?
- How to place an arrayplot/image on a GeoGraphics?
- What are the 270 mitzvot relevant today?
- Motion of the COM of 2-body system
- AM-GM inequality (but equality cannot be attained)
- The Fourth Daughter
- Has a tire ever exploded inside the Wheel Well?
- Where does the energy in ion propulsion come from?
- Is there a phrase for someone who's really bad at cooking?
- What is the purpose of these 33-ohm series resistors on the RMII side of the LAN8742A?

IMAGES
VIDEO
COMMENTS
This tutorial explains how to write a null hypothesis, including several step-by-step examples.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis
Formulating the Alternate Hypothesis The alternate hypothesis (H1) represents what you're trying to demonstrate, such as a significant effect or difference between groups. It's the claim that will be accepted if the evidence against the null hypothesis is strong enough. Crafting this hypothesis is a pivotal step in how to write a thesis proposal, as it guides the direction of your research.
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test. When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant.
Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Start by recognizing that the basic definition of "null" is "none" or "zero"—that's your biggest clue as to what a null hypothesis should say. Keep reading to learn everything you need to know about the null hypothesis, including how it relates to your research ...
The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.
Basic definitions. The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise. The statement being tested in a test of statistical significance is called the null ...
Key Takeaways The null hypothesis is a foundational element of statistical testing, positing no effect or difference, against which research findings are compared. Formulating a null hypothesis requires a clear understanding of the research question and a precise statement that can be empirically tested. Testing the null hypothesis involves collecting data and using statistical methods to ...
They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints. H0, the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
The concept of the null hypothesis is a cornerstone of statistical hypothesis testing. In the article 'Formulating a Null Hypothesis: Key Elements to Consider,' we delve into what a null hypothesis is, why it's crucial for research, and how to properly formulate one. This article offers a comprehensive guide for researchers and students alike, providing the necessary tools to craft a null ...
Null Hypothesis Overview The null hypothesis, H 0 is the commonly accepted fact; it is the opposite of the alternate hypothesis. Researchers work to reject, nullify or disprove the null hypothesis. Researchers come up with an alternate hypothesis, one that they think explains a phenomenon, and then work to reject the null hypothesis. Read on or watch the video for more information.
H0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt. Ha: The alternative hypothesis: It is a claim about the population that is contradictory to H0 and what we conclude when we reject H0. Since the ...
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
10.1 - Setting the Hypotheses: Examples A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations ...
A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection. Example: Hypothesis
A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
The null hypothesis is a hypothesis in which the sample observation results from chance. Learn the definition, principles, and types of the null hypothesis at BYJU'S.
The null and alternative hypothesis In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population.
The null hypothesis and alternative hypothesis are required to be fragmented properly before the data collection and interpretation phase in the research. Well fragmented hypotheses indicate that the researcher has adequate knowledge in that particular area and is thus able to take the investigation further because they can use a much more systematic system. It gives direction to the ...
The null hypothesis and alternative hypothesis are cornerstones in statistics and hypothesis testing. They represent a methodology used to validate or refute claims about a population based on sample data. The process involves assuming the null hypothesis is true and using statistical analysis to test if the observed data fit this assumption. This article delves into the key roles ...
The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.
For example, if you compare multiple methods on efficiency, you don't have to hypothesize beforehand which one is going to be the best. But the statistical test you use for comparison, will imply a "null hypothesis" that there is no real difference between all methods. Also this is "formulating a hypothesis" merely by the choice of analysis tools.